OCR Specification focus:
‘Use 1/T = f and v = fλ for waves.’
Understanding Time and Wave Equations
Waves are fundamental to the transmission of energy through space and matter, and their behaviour can be described mathematically. The time and wave equations link measurable quantities such as frequency, period, wavelength, and wave speed. Understanding these relationships allows physicists to predict how waves propagate, interact with materials, and transfer energy across different media.
This section introduces the key time and wave equations essential to describing the motion of progressive waves, forming a vital foundation for all later studies in wave physics.
The Relationship Between Time and Frequency
The time period (T) and frequency (f) describe the temporal characteristics of a wave. These quantities are inversely related — one defines the duration of a single cycle, while the other measures how many cycles occur per second.
Time Period (T): The time taken for one complete oscillation or cycle of the wave to pass a fixed point. Measured in seconds (s).
Frequency (f): The number of complete wave cycles passing a fixed point each second. Measured in hertz (Hz), where 1 Hz = 1 cycle per second.
The relationship between them is given by the time equation.
EQUATION
—-----------------------------------------------------------------
Time–Frequency Relationship
f = 1 / T
f = frequency (Hz)
T = period (s)
—-----------------------------------------------------------------
In a practical sense, if the period of a wave decreases, its frequency increases — meaning the source oscillates faster. This inverse relationship is fundamental in all types of waves, from sound and water waves to electromagnetic radiation.
Wave Speed and the Wave Equation
The wave equation relates a wave’s speed, frequency, and wavelength. This relationship allows us to calculate how quickly energy or information is transmitted through a medium.
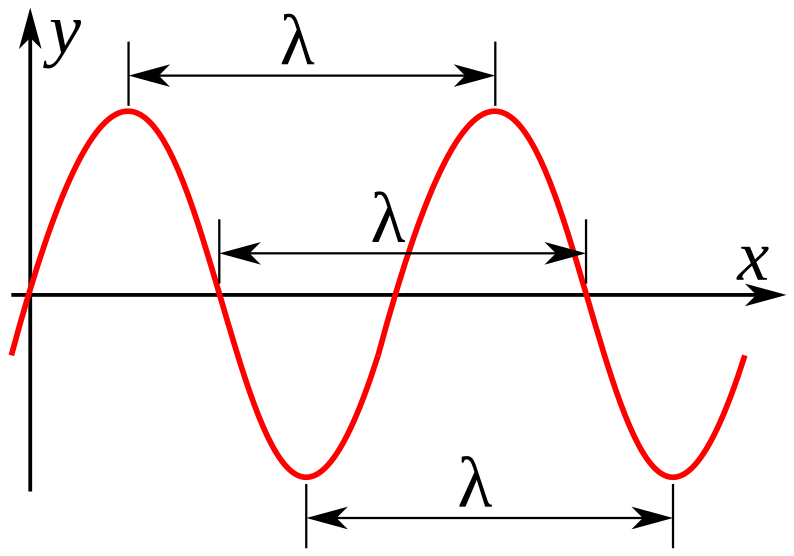
A sinusoidal wave with the wavelength (λ) marked between points in phase (crest-to-crest, trough-to-trough, or equivalent). This visual anchors v = fλ by showing the spatial period a wave travels in one cycle. Extra details beyond the syllabus are not included. Source.
Wavelength (λ): The distance between two consecutive points that are in phase on a wave (e.g., crest to crest or compression to compression). Measured in metres (m).
Wave Speed (v): The rate at which the wave propagates through the medium. Measured in metres per second (m s⁻¹).
EQUATION
—-----------------------------------------------------------------
Wave Equation
v = f λ
v = wave speed (m s⁻¹)
f = frequency (Hz)
λ = wavelength (m)
—-----------------------------------------------------------------
This equation shows that a wave’s speed is directly proportional to both its frequency and wavelength. If the frequency increases while speed remains constant, the wavelength must shorten, and vice versa.
Interpreting the Wave Equation
The wave equation is applicable to all mechanical and electromagnetic waves, provided the wave propagates in a uniform medium. It reveals several important principles:
Constant medium, constant speed: In a single medium, wave speed depends only on the properties of that medium — not on the frequency or wavelength separately.
Changing medium, changing speed: When a wave passes from one material to another (for example, air to glass), its speed and wavelength change, but its frequency remains constant.
Proportional relationship: Doubling the frequency doubles the wave speed only if wavelength remains constant, which typically occurs when the medium itself determines v.
Understanding how these variables interact helps explain phenomena such as refraction (where a change in speed causes bending of the wave path).
Practical Interpretation of Period and Frequency
To visualise the connection between period and frequency, consider observing a wave on an oscilloscope or through time-based measurement.
A long period corresponds to slow oscillations (low frequency).
A short period corresponds to rapid oscillations (high frequency).
When plotting a wave against time, the period can be directly read as the time between successive crests. This relationship is crucial in experimental physics, especially when determining unknown frequencies of sound or electromagnetic waves.
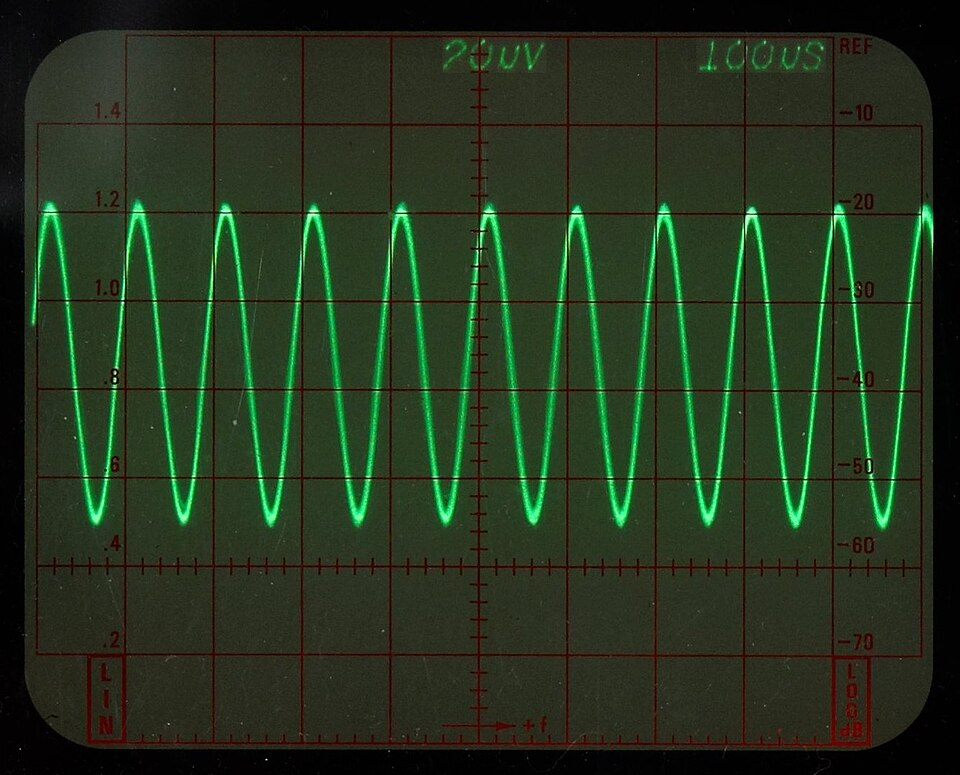
An oscilloscope trace of a 10 kHz sine wave. The timebase setting (100 μs per division) is shown along the screen edge, indicating how period T can be read from the horizontal graticule and converted to frequency f via f = 1/T. The image includes extra real-world detail (vertical scale and instrument model), which is not required by the syllabus but aids interpretation. Source.
Combining the Time and Wave Equations
The time and wave equations are often used together. Substituting the expression for frequency into the wave equation gives a new form linking wave speed directly to wavelength and period:
EQUATION
—-----------------------------------------------------------------
Combined Form
v = λ / T
v = wave speed (m s⁻¹)
λ = wavelength (m)
T = period (s)
—-----------------------------------------------------------------
This form is particularly useful when the period of oscillation is known but the frequency is not directly measured. It also reinforces that wave speed is determined by how far a wavefront travels in one period.
Application to Different Types of Waves
Mechanical Waves
Mechanical waves, such as sound or waves on a string, require a medium to propagate. Their wave speed depends on material properties like tension, density, and elasticity.
For example:
Sound travels faster in solids than in gases because particles are more tightly coupled.
In a stretched string, increasing tension raises wave speed, while increasing mass per unit length lowers it.
Electromagnetic Waves
Electromagnetic waves, such as light, do not require a medium. Their speed in a vacuum is constant and denoted by c = 3.0 × 10⁸ m s⁻¹.
When light enters a different medium (like water or glass), its speed changes according to the material’s refractive index, yet the frequency remains constant. The resulting wavelength change explains optical refraction.
Understanding Units and Measurement
To use the time and wave equations accurately, attention to units is vital:
Wavelength (λ) → metres (m)
Frequency (f) → hertz (Hz)
Period (T) → seconds (s)
Wave speed (v) → metres per second (m s⁻¹)
Because 1 Hz = 1 s⁻¹, the equation v = fλ has consistent dimensional balance:
m s⁻¹ = s⁻¹ × m, confirming its validity.
Linking Time, Frequency, and Energy
Although not explicitly part of this subsubtopic, understanding that frequency also connects to wave energy deepens physical insight. For example, in electromagnetic waves, energy is proportional to frequency. While the time and wave equations describe spatial and temporal characteristics, this connection underlines why high-frequency radiation (like gamma rays) carries more energy than low-frequency waves (like radio waves).
Summary of Relationships
To consolidate the core relationships:
f = 1 / T — frequency and period are inversely related.
v = fλ — wave speed equals frequency multiplied by wavelength.
v = λ / T — combining both gives a direct link between wavelength and period.
Each of these relationships underpins the study of all waves and is essential for experimental and theoretical analysis across the OCR A-Level Physics course.
FAQ
The wave equation v = fλ applies universally, but the wave speed (v) depends on the medium’s properties.
In air, speed is influenced by temperature, humidity, and pressure — warmer air allows faster sound propagation due to increased molecular energy.
In water or solids, wave speed increases because particles are more tightly packed, allowing energy to transfer more efficiently.
Although the frequency (f) remains constant when a wave moves between media, the wavelength (λ) changes proportionally to the new speed.
When a wave crosses a boundary, its speed and wavelength may change, but the frequency is fixed by the source.
The source determines how many oscillations occur per second, and this doesn’t change simply because the medium changes.
For example, a light wave moving from air into glass slows down and its wavelength decreases, but the frequency — set by the original light source — remains constant.
Several factors can introduce error in oscilloscope-based frequency measurements:
Incorrect timebase setting may make it hard to view a full cycle accurately.
Parallax error when reading graticule divisions by eye.
Signal noise or distortion can make the waveform’s start and end points unclear.
Poor calibration of the oscilloscope leads to inaccurate time-per-division values.
Using a stable waveform, clear triggering, and digital measurement functions can significantly improve accuracy.
The time period (T) measures how long one complete cycle takes. The phase difference describes how much one wave leads or lags another in its oscillation.
They are related through the equation:
Phase difference (in degrees) = (time difference / period) × 360°.
Phase difference helps explain interference and synchronisation between waves, while the period defines one full oscillation’s duration.
One method involves measuring wavelength and frequency separately:
Use a signal generator and loudspeaker to produce a sound wave of known frequency.
Place microphones a known distance apart along the wave’s path.
Measure the phase or time difference between signals received by the microphones.
Use v = fλ, where λ is the measured wavelength.
This technique provides an experimental verification of the time and wave equations for sound waves.
Practice Questions
Question 1 (2 marks)
A sound wave has a frequency of 500 Hz and a wavelength of 0.68 m.
(a) Calculate the speed of the sound wave.
(b) State the equation you have used.
Mark Scheme
Correct use of wave equation: v = fλ (1 mark)
Correct calculation: v = 500 × 0.68 = 340 m s⁻¹ (1 mark)
Question 2 (5 marks)
A student uses an oscilloscope to investigate a signal from a signal generator. The time base is set to 0.5 ms per division, and one complete cycle of the waveform occupies 4 divisions on the screen. The signal passes through a loudspeaker that emits sound waves into air, where the speed of sound is 340 m s⁻¹.
(a) Determine the period and frequency of the signal. (2 marks)
(b) Calculate the wavelength of the sound produced. (2 marks)
(c) Explain how the student could confirm that the sound wave and the electrical signal from the generator have the same frequency. (1 mark)
Mark Scheme
(a)
Period = 4 × 0.5 ms = 2.0 ms = 2.0 × 10⁻³ s (1 mark)
Frequency = 1 / T = 1 / (2.0 × 10⁻³) = 500 Hz (1 mark)
(b)
Correct use of v = fλ (1 mark)
λ = 340 / 500 = 0.68 m (1 mark)
(c)
Measure both frequencies using the oscilloscope and compare; they should be equal if the loudspeaker output matches the electrical signal (1 mark)

