OCR Specification focus:
‘Explain reflection, refraction, polarisation, diffraction; intensity ∝ amplitude²; I = P/A.’
Wave phenomena describe how waves interact with boundaries, obstacles, and each other, revealing essential properties of energy transfer, direction change, and amplitude behaviour in various physical contexts.
Reflection
Reflection occurs when a wave encounters a boundary between two different media and some or all of the wave energy is returned into the original medium. For instance, light reflecting from a mirror or sound reflecting as an echo are classic examples. Reflection obeys predictable geometric laws that apply to all types of waves, including mechanical and electromagnetic forms.
Reflection: The process by which a wave bounces back from a surface or boundary into the medium from which it came.
The law of reflection states that the angle of incidence equals the angle of reflection, both measured from the normal (a line perpendicular to the surface). In regular reflection, smooth surfaces produce clear images because all reflected rays are parallel. In diffuse reflection, rough surfaces scatter the waves in many directions, preventing image formation but still allowing detection, such as light reflecting from paper.
Reflection is an important concept in acoustics, seismology, and optics, where it aids in the design of devices such as periscopes, reflectors, and sonar systems.
Refraction
Refraction occurs when a wave passes from one medium to another and changes direction due to a change in wave speed. This happens because the wave’s speed depends on the properties of the medium.
Refraction: The change in direction of a wave when it crosses a boundary between media in which its speed is different.
When light enters a denser medium, it slows down and bends towards the normal. When it passes into a less dense medium, it speeds up and bends away from the normal. This behaviour follows Snell’s Law, which relates the sine of the angle of incidence and refraction to the ratio of wave speeds or refractive indices.
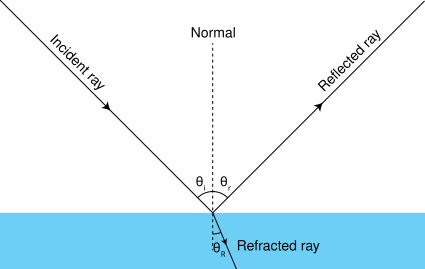
Ray diagram at a flat boundary showing the incident ray, reflected ray (with angle equal to the angle of incidence), and refracted ray obeying Snell’s law. The normal and media are clearly indicated to emphasise angle measurements. This directly illustrates direction change at a material boundary. Source.
EQUATION
—-----------------------------------------------------------------
Snell’s Law (n₁, n₂, i, r) = n₁ sin i = n₂ sin r
n = Refractive index (dimensionless)
i = Angle of incidence (°)
r = Angle of refraction (°)
—-----------------------------------------------------------------
Refraction explains many everyday phenomena such as the apparent bending of a straw in water and the focusing ability of lenses in optical instruments. It is also crucial in understanding rainbows and atmospheric mirages.
Polarisation
Only transverse waves can be polarised, because their oscillations occur perpendicular to the direction of energy transfer. Longitudinal waves, such as sound, cannot be polarised since their oscillations are parallel to the direction of propagation.
Polarisation: The restriction of the oscillations of a transverse wave to a single plane perpendicular to the direction of wave travel.
Light from most sources is unpolarised, meaning its electric field oscillates in multiple planes. Passing such light through a polarising filter allows only one plane of vibration to pass, producing plane-polarised light.
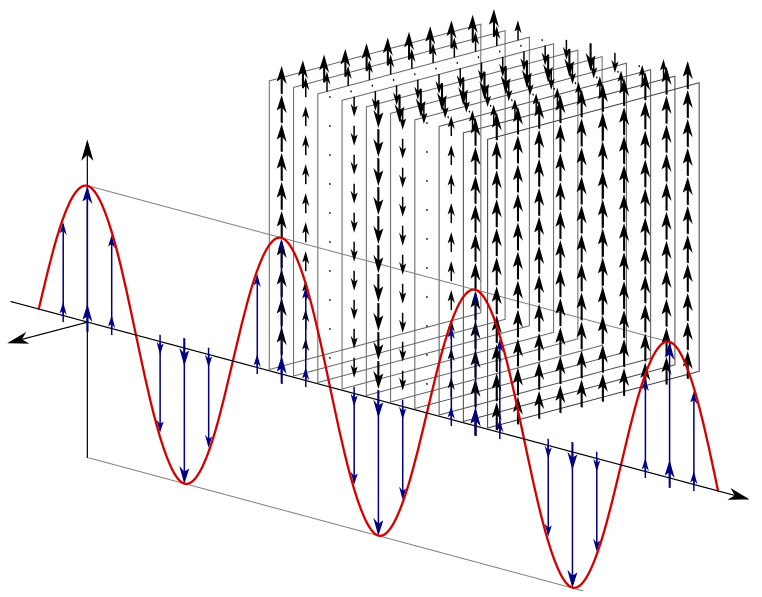
Linearly polarised electromagnetic wave with the electric field oscillating in one plane perpendicular to the direction of propagation. The magnetic field is shown as the perpendicular companion field. This clarifies why only transverse waves can be polarised. Source.
If two polarising filters are placed at right angles, almost no light is transmitted. This demonstrates how polarisation filters work in devices such as sunglasses, camera lenses, and LCD screens.
Microwave experiments can demonstrate polarisation using metal grille filters, which absorb the component of the wave’s electric field aligned with the wires while transmitting the perpendicular component. This shows that electromagnetic waves are transverse and that their electric field direction determines their polarisation.
Diffraction
Diffraction refers to the spreading of waves when they pass through a gap or move around an obstacle. The extent of diffraction depends on the relationship between the wavelength and the size of the gap or obstacle.
Diffraction: The spreading of waves as they pass through an aperture or around the edges of an obstacle.
If the gap is much larger than the wavelength, diffraction is minimal and waves pass mostly straight through. When the gap is comparable to the wavelength, diffraction is significant, and the wave spreads widely. Diffraction allows sound to be heard around corners and light to spread through narrow slits in optical experiments. For electromagnetic waves, diffraction is observable in radio and microwave applications, where long wavelengths make the effect more pronounced.
Diffraction patterns consist of alternating bright and dark regions due to interference between diffracted waves. This phenomenon underpins many experimental investigations into the wave nature of light and forms the basis of technologies such as diffraction gratings used in spectroscopy.
Wave Intensity
The intensity of a wave quantifies the energy transferred per second per unit area perpendicular to the wave’s direction of propagation. It indicates how much power a wave delivers and is directly related to the amplitude of the wave.
EQUATION
—-----------------------------------------------------------------
Intensity (I) = Power (P) / Area (A)
I = Intensity (W m⁻²)
P = Power of the wave source (W)
A = Area over which the power is spread (m²)
—-----------------------------------------------------------------
For progressive waves, intensity is proportional to the square of amplitude (I ∝ A²). This means that doubling the amplitude results in a fourfold increase in intensity. The relationship is fundamental to understanding loudness in sound waves, brightness in light waves, and the energy carried by all types of waves.
In spherical wavefronts, such as those from a point source, intensity decreases with distance as the wave energy spreads over a larger area. This follows an inverse square law, meaning intensity falls proportionally to 1/r², where r is the distance from the source.
Connections Between Wave Phenomena and Intensity
Reflection, refraction, polarisation, and diffraction all influence wave energy distribution and therefore affect observed intensity. For instance:
During reflection, some energy is absorbed, and some is returned, altering intensity at the surface.
In refraction, intensity may decrease due to partial reflection or absorption within the medium.
Polarisation filters reduce intensity by removing components of the wave’s oscillation.
Diffraction spreads energy over a wider region, reducing intensity in any one direction.
Understanding these interrelated phenomena allows physicists to predict how waves behave in complex systems, supporting applications across optics, communications, acoustics, and quantum technologies.
FAQ
The amount of diffraction depends strongly on the relationship between wavelength and the size of the gap or obstacle.
When the wavelength is much smaller than the gap, waves pass through with little spreading.
When the wavelength is comparable to or larger than the gap, diffraction becomes significant and the waves spread widely.
This explains why radio waves (with long wavelengths) can bend around buildings, whereas light (with short wavelengths) cannot.
Transverse waves have oscillations that occur perpendicular to the direction of energy transfer, so their vibrations can be restricted to a single plane.
Longitudinal waves, such as sound, vibrate parallel to their direction of travel. Since their motion is already confined to one direction, there is no perpendicular component to filter or restrict, making polarisation impossible for these waves.
When a wave crosses a boundary between two media:
Wave speed changes because the medium’s density or optical properties differ.
Frequency remains constant because it is determined by the source.
Wavelength must therefore change to maintain the relationship v = fλ.
If the wave slows down, its wavelength shortens; if it speeds up, its wavelength increases.
At a boundary, part of the wave’s energy is reflected and part transmitted (refracted).
The transmitted portion may lose energy through:
Absorption within the new medium.
Scattering or partial reflection at microstructures.
Divergence of energy due to refraction angle changes.
Hence, reflected and refracted waves typically carry less intensity than the original wave.
When unpolarised light passes through a polarising filter, only one plane of oscillation is transmitted.
If electromagnetic waves were longitudinal, their oscillations would occur along the direction of propagation and could not be selectively filtered. The ability to block and transmit light based on its vibration plane provides direct evidence that light — and all electromagnetic radiation — is a transverse wave.
Practice Questions
Question 1 (2 marks)
State what is meant by diffraction and describe one condition that increases the extent of diffraction of a wave.
Mark Scheme:
1 mark: Correct definition of diffraction — spreading of waves as they pass through a gap or around an obstacle.
1 mark: Correct condition — diffraction is greatest when the gap or obstacle size is comparable to the wavelength of the wave.
Question 2 (5 marks)
A beam of unpolarised light passes through two polarising filters.
(a) Explain how the first filter affects the light. (2 marks)
(b) The second filter is rotated so that its transmission axis is at 90° to that of the first. Describe and explain what is observed. (3 marks)
Mark Scheme:
(a)
1 mark: The first polarising filter only allows vibrations (electric field oscillations) in one plane to pass through.
1 mark: The emerging light is plane-polarised.
(b)
1 mark: When the second filter is at 90°, little or no light is transmitted.
1 mark: The second filter blocks oscillations not aligned with its transmission axis.
1 mark: Correct reasoning — the transmission axes of the two filters are perpendicular, so the component of the electric field that can pass through the second filter is zero.

