Electromagnetic (EM) waves span an immense range of wavelengths, from kilometres in radio waves to less than a picometre in gamma rays. Understanding these orders of magnitude helps classify EM waves, appreciate their varied applications, and predict their interactions with matter.

The Electromagnetic Spectrum Overview

The electromagnetic spectrum includes all possible frequencies of electromagnetic radiation. Each region corresponds to a range of wavelengths and frequencies but shares the same fundamental wave nature — oscillating electric and magnetic fields that propagate through space at the speed of light in a vacuum (c ≈ 3.00 × 10⁸ m s⁻¹).

Despite differing enormously in scale, all EM waves exhibit the same basic behaviour, including reflection, refraction, and diffraction. Their classification depends solely on wavelength (λ) or frequency (f), linked by the fundamental relationship:

EQUATION
—-----------------------------------------------------------------
Wave Speed Equation (v = fλ)
v = wave speed (m s⁻¹)
f = frequency (Hz)
λ = wavelength (m)
—-----------------------------------------------------------------

In a vacuum, v = c, so longer wavelengths correspond to lower frequencies and vice versa.

Orders of Magnitude across the Spectrum

To “recall approximate wavelength orders” means to know the typical powers of ten that describe the wavelength ranges of each EM band. The spectrum can be ordered from the longest to the shortest wavelengths as follows:

• Radio waves: 10³ to 10⁻¹ m

• Microwaves: 10⁻¹ to 10⁻³ m

• Infrared (IR): 10⁻³ to 7 × 10⁻⁷ m

• Visible light: 7 × 10⁻⁷ to 4 × 10⁻⁷ m

• Ultraviolet (UV): 4 × 10⁻⁷ to 10⁻⁸ m

• X-rays: 10⁻⁸ to 10⁻¹¹ m

• Gamma rays: <10⁻¹¹ m

These are approximate, overlapping boundaries — real sources emit a continuous range of wavelengths rather than distinct categories.

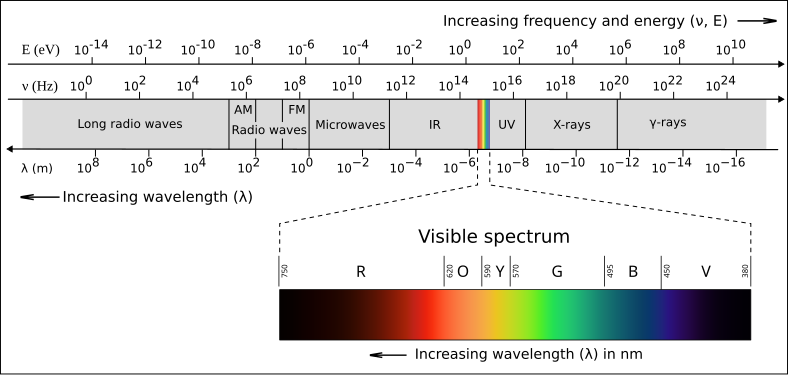
A clean diagram of the electromagnetic spectrum from radio to gamma rays, labelled by wavelength (m), frequency (Hz), and photon energy (eV). The powers-of-ten scale highlights how wavelength decreases by orders of magnitude across the spectrum. This image includes an energy axis in addition to wavelength/frequency; that extra detail is useful context but not required by the syllabus. Source.

Radio Waves (λ ≈ 10³ m to 10⁻¹ m)

Radio waves have the longest wavelengths and lowest frequencies in the spectrum.
They are produced by oscillating electrical currents in antennas and are used for broadcasting, communication, and radar.
Because of their long wavelength, they can diffract around obstacles and reflect off the ionosphere, allowing long-distance transmission.

Microwaves (λ ≈ 10⁻¹ m to 10⁻³ m)

Microwaves are shorter than radio waves but still relatively long compared with visible light.
They are used in satellite communication, microwave ovens, and Doppler radar systems. Their wavelengths correspond to sizes comparable to water molecules, making them effective for heating food by causing molecular rotation.

Infrared Radiation (λ ≈ 10⁻³ m to 7 × 10⁻⁷ m)

Infrared waves are emitted by warm objects, corresponding to the thermal radiation humans can sense as heat.
Applications include night-vision cameras, remote controls, and thermal imaging.
Their wavelengths are slightly longer than visible red light, allowing efficient energy transfer without ionisation.

Visible Light (λ ≈ 7 × 10⁻⁷ m to 4 × 10⁻⁷ m)

This is the narrow band detectable by the human eye.
The visible spectrum runs from red (longest wavelength) to violet (shortest wavelength).

A linear bar of the visible spectrum labelled in nanometres, showing the continuous transition from approximately 700 nm (red) to 400 nm (violet). This focuses purely on the visible range to reinforce the typical 10⁻⁷ m order of magnitude. The diagram is intentionally minimal, avoiding applications or unrelated details. Source.

Though it spans less than a factor of two in wavelength, this region contains all perceived colours and is essential to human vision and photosynthesis.

Ultraviolet Radiation (λ ≈ 4 × 10⁻⁷ m to 10⁻⁸ m)

Ultraviolet (UV) lies beyond violet light and possesses higher frequencies and energies.
It can cause ionisation in atoms and molecules, making it biologically hazardous in excess.
However, it is useful for sterilisation, fluorescent lighting, and detecting forged banknotes.
The atmosphere partially absorbs UV radiation, especially by the ozone layer.

X-Rays (λ ≈ 10⁻⁸ m to 10⁻¹¹ m)

X-rays have much shorter wavelengths, giving them high photon energies.
They are produced when high-speed electrons strike metal targets, leading to medical imaging and crystal diffraction studies.
Because they can penetrate soft tissue but are absorbed by bone, they reveal internal structures clearly.

Gamma Rays (λ < 10⁻¹¹ m)

Gamma rays are the shortest-wavelength and highest-energy electromagnetic waves.
They originate from nuclear decay, cosmic phenomena, and particle interactions.
Their extreme energy allows deep penetration through matter, useful in cancer radiotherapy but also potentially dangerous to living cells.

Relationship Between Wavelength and Energy

As wavelength decreases across the EM spectrum, frequency and therefore photon energy increase. The relationship is given by:

EQUATION
—-----------------------------------------------------------------
Photon Energy (E = hf)
E = photon energy (J)
h = Planck’s constant (6.63 × 10⁻³⁴ J s)
f = frequency (Hz)
—-----------------------------------------------------------------

This explains why gamma rays and X-rays are ionising — their photons carry enough energy to remove electrons from atoms. Conversely, radio waves are non-ionising, interacting primarily through oscillations of electric charges.

Scientific Use of Orders of Magnitude

Physicists often use orders of magnitude (powers of ten) to express large or small quantities efficiently. For EM waves, this helps:

• Estimate energy levels: A tenfold decrease in wavelength corresponds to a tenfold increase in frequency.

• Predict interactions: Long wavelengths interact with macroscopic objects (antennas), while short wavelengths affect atomic or subatomic scales.

• Design experiments: Knowing wavelength orders determines appropriate apparatus — for example, diffraction gratings for visible light or crystal lattices for X-rays.

Logarithmic Representation

Because the EM spectrum spans about 20 orders of magnitude, logarithmic scales are often used to visualise it.
Each order of magnitude step corresponds to multiplying or dividing wavelength by ten.
For example:

• Radio (10⁰ m) → Microwave (10⁻² m) → Infrared (10⁻⁴ m) → Visible (10⁻⁶ m) → UV (10⁻⁷ m) → X-ray (10⁻¹⁰ m) → Gamma (10⁻¹² m).

This continuous progression illustrates the unified nature of electromagnetic radiation despite its diversity in practical applications.

Applications Linked to Wavelength Orders

• Communication: Radio and microwaves transmit data via amplitude or frequency modulation.

• Imaging: Infrared and visible light enable optical instruments and thermal cameras.

• Medical and scientific use: X-rays and gamma rays probe atomic structures and treat diseases.

• Environmental monitoring: UV and IR sensors analyse atmospheric composition and climate effects.

Each application exploits the specific interaction between wavelength and matter, showing how understanding the orders of magnitude guides technological development.