OCR Specification focus:
‘For light: n = c/v; n sin i is constant at a boundary between media.’
Refraction and refractive index describe how light changes direction and speed when passing between materials with different optical densities. Understanding these relationships is key to explaining many optical phenomena and technologies.
Refraction of Light
What is Refraction?
Refraction occurs when a wave passes from one medium into another and changes direction due to a change in wave speed. For example, when light travels from air into glass, it bends towards the normal, whereas moving from glass to air, it bends away from the normal.
This bending results from the change in the wave speed as the light enters a medium with a different optical density — a measure of how much a material slows down light.
Refraction: The change in direction of a wave as it passes across a boundary between two media due to a change in wave speed.
The Normal Line and Angles of Incidence and Refraction
To describe refraction, a normal line (a perpendicular to the boundary) is drawn.
The angle of incidence (i) is the angle between the incident ray and the normal.
The angle of refraction (r) is the angle between the refracted ray and the normal.
When light enters a denser medium (e.g. air to glass), i > r.
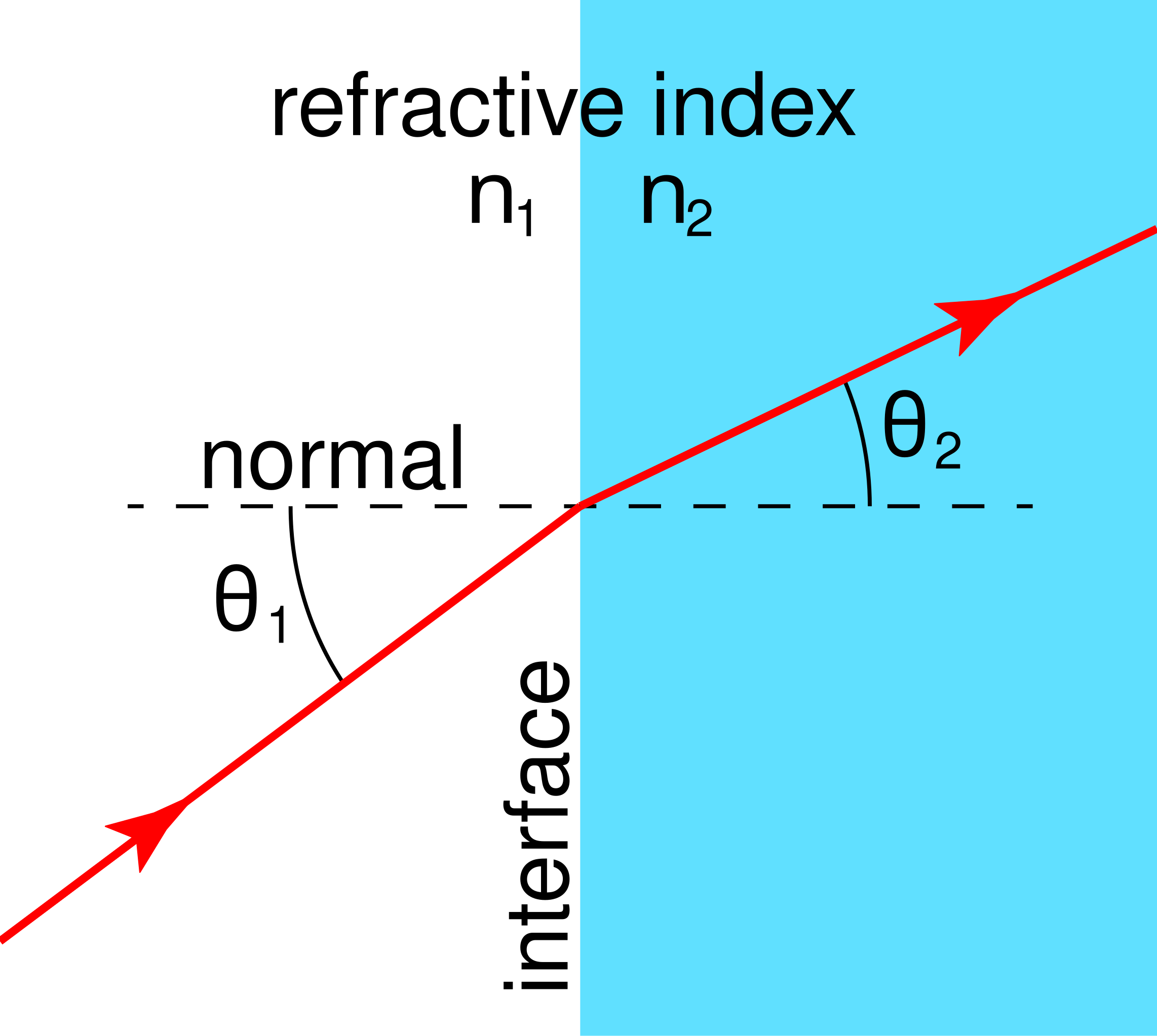
Diagram of refraction at a plane interface with the normal, incident ray, and refracted ray clearly labelled. The angles i and r are measured relative to the normal, illustrating bending towards or away from it depending on optical density. This aligns with the OCR requirement to understand light refraction at a boundary. Source.
When it enters a less dense medium (e.g. glass to air), i < r.
Wave Speed and Optical Density
Change in Wave Speed
The speed of light in a vacuum (c) is approximately 3.00 × 10⁸ m s⁻¹. When light enters any other medium, it slows down because interactions between the light wave and the atoms in the material cause delays in the wave’s propagation.
Optical density is not the same as physical density — for example, water and glass both slow light differently despite similar physical densities. The degree to which a medium slows light is quantified by its refractive index.
Refractive Index
Definition and Concept
Refractive Index (n): The ratio of the speed of light in a vacuum to the speed of light in the medium.
EQUATION
—-----------------------------------------------------------------
Refractive Index (n) = c / v
c = speed of light in a vacuum (3.00 × 10⁸ m s⁻¹)
v = speed of light in the medium (m s⁻¹)
—-----------------------------------------------------------------
The larger the refractive index, the slower light travels in that medium. For example, typical refractive indices are:
Air ≈ 1.00
Water ≈ 1.33
Glass ≈ 1.50
Diamond ≈ 2.42
These values show that light travels more slowly and bends more strongly in materials with higher refractive indices.
Between different materials, refraction follows a constant relationship given by Snell’s law.
Snell’s Law
When light passes between two media, the product of the refractive index and the sine of the angle of incidence remains constant.
EQUATION
—-----------------------------------------------------------------
Snell’s Law: n₁ sin i = n₂ sin r
n₁ = refractive index of the first medium (no unit)
i = angle of incidence (degrees or radians)
n₂ = refractive index of the second medium (no unit)
r = angle of refraction (degrees or radians)
—-----------------------------------------------------------------
This relationship allows one to predict how much a ray of light bends when entering a new medium.
A concise Snell’s law diagram linking the angles i and r to the refractive indices n₁ and n₂. It shows how the product n sin θ remains constant across a boundary, as required by the specification. Clean labelling keeps focus on the law without unnecessary extras. Source.
If n₂ > n₁, light bends towards the normal; if n₂ < n₁, it bends away from the normal.
Constant Relationship at a Boundary
According to the OCR specification, n sin i remains constant at a boundary between two media. This principle underpins the concept of reversibility of light paths — if the direction of travel is reversed, the same path is followed but in the opposite direction.
This constancy can be verified experimentally using light boxes, rectangular glass blocks, and protractors to measure i and r, confirming that the ratio sin i / sin r equals a constant — the refractive index.
Physical Explanation of Refraction
Refraction occurs because the wavefronts of light slow down or speed up upon crossing a boundary:
When entering a denser medium, the near edge of the wavefront slows first, causing the wave to bend towards the normal.
When leaving a denser medium, the opposite edge speeds up first, bending the wave away from the normal.
This behaviour applies to all wave types, but the OCR specification focuses specifically on light waves.
Practical Implications and Optical Applications
Everyday Examples
Refraction explains several common observations:
Objects appear bent or displaced under water due to the change in light direction.
Lenses in glasses and cameras use refraction to focus light.
Rainbows occur because sunlight refracts and disperses in water droplets.
Lenses and Image Formation
Lenses rely on controlled refraction to converge or diverge light rays. The curvature of a lens and its refractive index determine its focal length — the distance at which light rays meet (or appear to meet). A higher refractive index allows the same focusing power with a thinner lens.
Measuring Refractive Index
Experimental Methods
Students can measure the refractive index of glass using a ray box and protractor:
Draw a normal to the surface of a glass block.
Direct an incident ray at a known angle i.
Measure the angle of refraction r inside the block.
Calculate n = sin i / sin r.
Alternatively, for transparent liquids or solids, optical instruments such as a refractometer can provide direct measurements by detecting light deviation.
Significance in Physics
Refraction is essential for understanding how light interacts with materials and underpins many optical technologies, including microscopes, telescopes, cameras, and optical fibres.
The refractive index provides a direct link between wave speed and optical behaviour, encapsulated by the OCR specification relationship:
EQUATION
—-----------------------------------------------------------------
Refractive Index Relationship: n = c / v
n sin i = constant at a boundary
—-----------------------------------------------------------------
This dual expression summarises the fundamental principles that govern the behaviour of light as it travels between media of differing optical densities.
FAQ
The refractive index depends on both the composition of the material and the wavelength of the light.
Materials with more tightly bound electrons interact more strongly with light, increasing optical density and thus refractive index.
The temperature and pressure of a medium can also slightly alter the refractive index, as they change the material’s density.
Refractive index decreases slightly for longer wavelengths (red light) — a phenomenon known as dispersion, where different wavelengths refract by different amounts.
Refraction involves a change in wave speed as light passes from one medium to another. In wave theory, this change in speed leads to a change in direction predicted by Huygens’ principle, which describes how each point on a wavefront acts as a source of secondary wavelets.
If light were purely particle-based, it would not naturally explain the smooth bending of rays at a boundary — the wave model accurately predicts this behaviour through interference of these secondary wavelets.
When light enters a denser medium, its speed decreases, but its frequency remains constant. Because wave speed (v) = frequency (f) × wavelength (λ), a lower speed means a shorter wavelength.
This compression of wavelength within a denser medium is visible in wavefront diagrams and is the key reason the direction of light changes.
Yes. Refraction can also occur:
In gases, such as air layers of different temperatures in the atmosphere, producing mirages.
In plasmas, where light interacts with free electrons and experiences strong refraction.
Even in biological materials like the cornea of the eye, where refraction directs light onto the retina.
Any boundary between regions with different light speeds can cause refraction, regardless of whether the materials are solid, liquid, or gaseous.
Different colours (wavelengths) of light interact differently with the electrons in a medium. Shorter wavelengths, such as blue and violet, are slowed more than longer red wavelengths.
As a result, blue light refracts more strongly, leading to dispersion effects in lenses and prisms. This wavelength-dependent variation of refractive index is why a prism separates white light into its component colours.
Practice Questions
Question 1 (2 marks)
A ray of light passes from air into glass at an angle of incidence of 35°. The angle of refraction is measured to be 22°.
Calculate the refractive index of the glass.
Mark scheme:
Correct use of Snell’s law: n = sin i / sin r (1 mark)
Substitution and correct numerical answer: n = sin(35°)/sin(22°) ≈ 1.52 (1 mark)
Question 2 (5 marks)
A student investigates how the angle of refraction of light varies as it passes from air into water.
They record the angle of incidence and corresponding angle of refraction for several values.
(a) Explain why the refracted ray bends towards the normal when entering the water. (2 marks)
(b) Describe how the student could use their results to determine the refractive index of water. (3 marks)
Mark scheme:
(a)
Light slows down as it enters a denser medium (1 mark)
Because the wavefronts are closer together in water, the ray bends towards the normal (1 mark)
(b)
Plot a graph of sin i (x-axis) against sin r (y-axis) (1 mark)
The gradient of the graph gives 1/n or n, depending on axes chosen (1 mark)
Calculate the refractive index using n = sin i / sin r or from the gradient of the line (1 mark)

