Graphical superposition methods allow physicists to visualise how waves combine at a point in space and time. By adding displacements graphically, the resultant wave form can be predicted with precision.

Understanding Superposition

The Principle of Superposition

When two or more waves overlap, the total displacement at any point is the vector sum of their individual displacements. This principle applies to all types of waves, including sound, light, and water waves.

This fundamental idea underpins interference, diffraction, and the formation of stationary waves. Graphical methods provide a practical way to represent and predict the results of wave interactions.

Representing Waves Graphically

Graphical Wave Representation

A wave can be represented on a displacement–distance or displacement–time graph. These show how displacement varies across space or time, respectively. Each point on the graph represents a particular position or instant for a particle in the medium.

When using graphical superposition:

• Both waves must be drawn on the same axes.

• Each wave’s displacement must be taken at corresponding points or times.

• The total displacement is found by adding or subtracting displacements at each point.

This approach works for any pair of waves of the same type, provided they exist in the same region simultaneously.

The Process of Graphical Superposition

Step-by-Step Method

To apply graphical superposition, follow these steps carefully:

1. Draw both waves on the same set of axes, ensuring their displacements are plotted on the same scale.

2. Choose a series of positions or times where displacements will be measured.

3. At each point, add (for in-phase displacements) or subtract (for opposite displacements) the amplitudes of the individual waves.

4. Plot the resultant displacement at each point to form the combined wave.

5. Connect the resultant points smoothly to reveal the overall wave pattern.

The accuracy of this process depends on consistent scaling and careful attention to phase relationships.

Understanding Phase and Its Role

Phase and Phase Difference

Phase describes the position of a point within one complete cycle of a wave. It is usually measured in degrees or radians.

If two waves are in phase, their peaks and troughs align, leading to maximum constructive interference. If they are out of phase by 180° (π radians), one wave’s peak aligns with the other’s trough, producing destructive interference.

Graphical methods make these relationships visually clear by showing how the waves overlap point by point.

Constructive and Destructive Addition

Visualising Interference Effects

Using graphical methods, two key interference outcomes can be identified:

• Constructive interference occurs when displacements are in the same direction, producing a larger resultant amplitude.

• Destructive interference occurs when displacements oppose each other, leading to reduction or cancellation.

At points between these extremes, the resultant amplitude lies somewhere between maximum and minimum, depending on the degree of phase difference.

Each resultant point on the graph shows the physical displacement of the medium where the waves meet.

Graphical Superposition in Practice

Equal Frequency and Amplitude Waves

When two waves of equal frequency and amplitude combine:

• If in phase, their amplitudes add, and the resultant amplitude is twice the original.

• If out of phase by 180°, they cancel completely, giving zero resultant displacement.

Graphically, this is seen as perfect reinforcement or complete flattening of the waveform, respectively. Intermediate phase differences yield intermediate resultant amplitudes.

Different Frequencies or Amplitudes

When two waves differ in frequency or amplitude, graphical addition produces complex resultant patterns. These may vary in time, showing beats or modulations in amplitude.

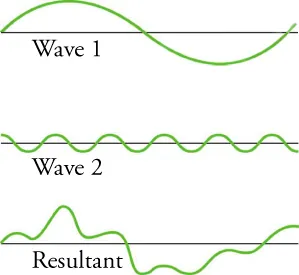
Two waves of different amplitude and frequency combine to form a non-sinusoidal resultant obtained by adding displacements point-by-point. This reinforces that superposition applies generally, not only to identical waves. Any extra references to standing waves or other phenomena on the page are beyond this subsubtopic and can be ignored. Source.

EQUATION
—-----------------------------------------------------------------
Beat Frequency (fᵦ) = |f₁ − f₂|
f₁, f₂ = Frequencies of the two combining waves (Hz)
—-----------------------------------------------------------------

Graphically, beats appear as a varying envelope amplitude, highlighting the periodic increase and decrease in intensity.

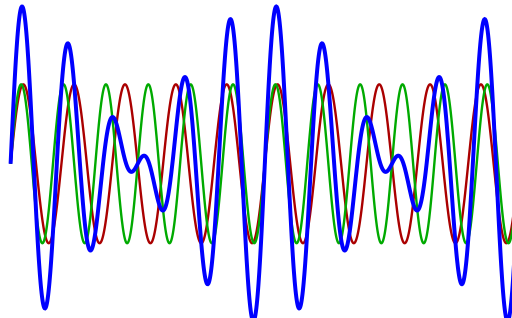
Two equal-amplitude waves with slightly different frequencies (red and green) superpose to produce a blue resultant whose amplitude rises and falls—the beat envelope. This directly illustrates the graphical signature of beats mentioned in the notes. The specific 5:6 frequency ratio shown is illustrative and not required by the syllabus. Source.

Vector Nature of Displacement

Considering Vector Addition

Because wave displacement has direction as well as magnitude, graphical superposition is effectively vector addition. For transverse waves, upward displacements are positive, downward are negative.
For longitudinal waves, forward compressions are treated as positive and rarefactions as negative. This ensures correct addition of displacements and accurate resultant waveforms.

Application to Multiple Waves

Extending the Method

While graphical superposition is often demonstrated for two waves, it can be extended to multiple overlapping waves. Each additional wave’s displacement is added sequentially at every point. The resulting waveform can become complex but follows the same principles:

• Displacements are added algebraically at each location or time.

• The resultant waveform reveals the combined effect of all contributors.

• Regular patterns may form if waves are coherent; irregular patterns result if they are not.

Graphical addition of coherent waves produces stable interference patterns, while incoherent waves yield fluctuating or averaged results.

Predicting Physical Outcomes

Using Graphs to Anticipate Behaviour

By using displacement–time or displacement–distance graphs, students can predict:

• Points of maximum and minimum displacement (antinodes and nodes in stationary contexts).

• Regions of constructive or destructive interference.

• Overall amplitude variations due to phase or frequency changes.

This makes graphical methods essential for visualising how real-world interference patterns arise in experiments involving light, sound, or microwaves.

Limitations of the Graphical Method

While the method is intuitive, it has some constraints:

• It becomes less precise when dealing with more than two or three waves.

• It assumes perfect coherence and neglects energy losses.

• It is mainly qualitative unless supported by mathematical analysis.

Nevertheless, it provides a powerful conceptual tool for visualising how waveforms interact, aligning perfectly with the OCR requirement to “use graphical methods to add wave displacements and predict outcomes.”