OCR Specification focus:
‘Relate constructive and destructive interference to path and phase difference conditions.’
Interference arises when two or more waves meet, creating a new resultant pattern of displacement. Understanding constructive and destructive interference reveals how waves combine to amplify or cancel each other’s effects.
Interference and Superposition
When two or more waves overlap in space, their displacements combine according to the principle of superposition. This principle is fundamental to understanding interference patterns in sound, light, and water waves.
Principle of Superposition: When two or more waves overlap, the resultant displacement at any point equals the vector sum of the displacements due to each wave.
The resulting pattern depends on the phase relationship between the waves. If they are in phase, the waves reinforce each other; if they are out of phase, they reduce or cancel one another.
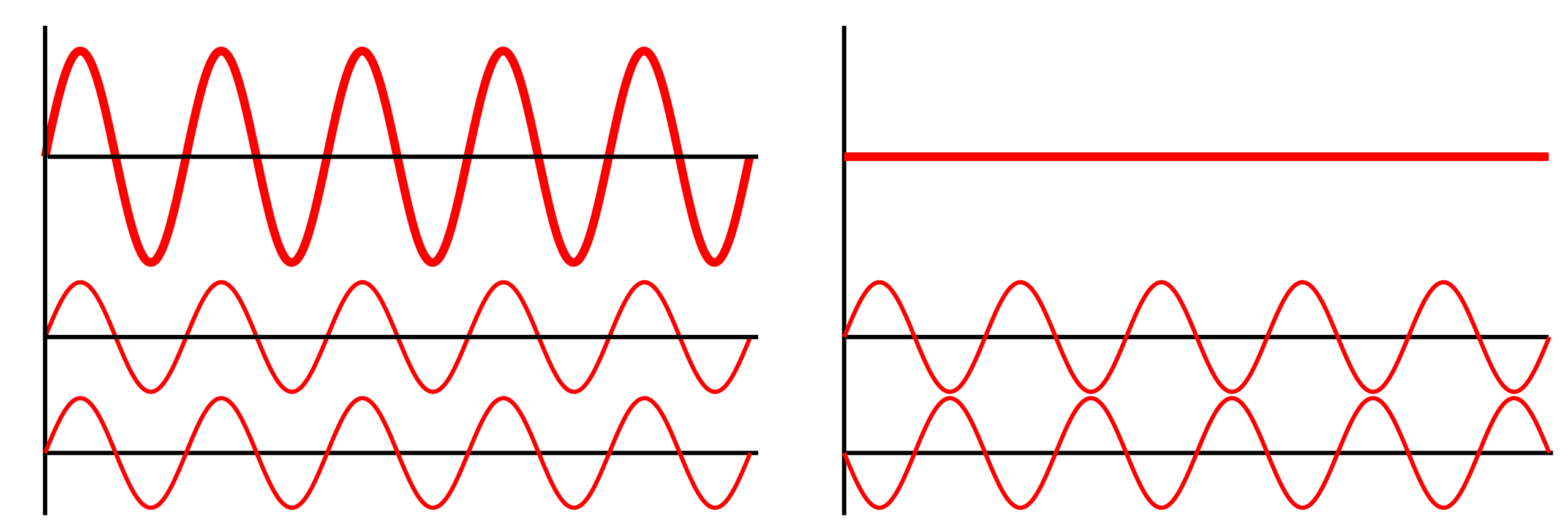
Two identical waves add in phase to produce a larger resultant amplitude (constructive interference) and 180° out of phase to cancel (destructive interference). The diagram isolates phase effects with minimal clutter, linking phase difference directly to amplitude outcomes. Source.
Phase Difference and Path Difference
Interference patterns depend on how the waves’ phases relate to each other at the point of overlap.
Phase Difference: The angular difference between the oscillations of two waves at a point, measured in radians or degrees, indicating how much one wave leads or lags another.
When waves start from coherent sources—meaning they have a constant phase relationship—the phase difference depends directly on the difference in the distance travelled, known as the path difference.
Path Difference: The difference in distance travelled by two waves from their sources to a common point.
The phase difference (ϕ) is linked to the path difference (Δx) by the relationship:
EQUATION
—-----------------------------------------------------------------
Phase Difference (ϕ) = (2π/λ) × Δx
ϕ = phase difference (radians)
λ = wavelength (metres)
Δx = path difference (metres)
—-----------------------------------------------------------------
A path difference corresponding to a whole number of wavelengths (nλ) results in constructive interference, whereas a difference of odd multiples of half wavelengths ((n + ½)λ) gives destructive interference.
Constructive Interference
Constructive interference occurs when waves arrive in phase—that is, their crests and troughs coincide. The individual displacements add together to form a resultant wave with greater amplitude than either of the original waves.
Constructive Interference: The process where two or more waves combine so that their displacements reinforce each other, producing a larger resultant amplitude.
This phenomenon explains bright fringes in light interference, loud regions in sound interference, or high points in water wave patterns.
For two waves of the same frequency and amplitude:
EQUATION
—-----------------------------------------------------------------
Condition for Constructive Interference
Path difference (Δx) = nλ, where n = 0, 1, 2, 3 …
—-----------------------------------------------------------------
At these points, the phase difference between the waves is a multiple of 2π radians, meaning they oscillate perfectly in synchrony.
In physical systems:
Light waves produce bright fringes on an interference pattern.
Sound waves generate louder zones, or antinodes, in air.
Microwave experiments show areas of maximum signal intensity on a detector.
Constructive interference demonstrates the wave nature of phenomena, particularly in double-slit and diffraction grating experiments.
Destructive Interference
Destructive interference occurs when two waves arrive completely out of phase—the crest of one coincides with the trough of the other, cancelling each other’s displacements.
Destructive Interference: The process where two waves combine with opposite displacements, causing partial or total cancellation of the resultant wave amplitude.
The resultant amplitude is reduced or, in perfect cancellation, becomes zero. This is the origin of dark fringes or silent points in interference patterns.
EQUATION
—-----------------------------------------------------------------
Condition for Destructive Interference
Path difference (Δx) = (n + ½)λ, where n = 0, 1, 2, 3 …
—-----------------------------------------------------------------
At these points, the phase difference is an odd multiple of π radians. The waves’ oscillations oppose one another exactly.
Physical examples include:
Dark fringes in optical interference experiments like Young’s double-slit setup.
Quiet regions in sound interference tests.
Zero-intensity zones in microwave interference patterns.
These patterns highlight how energy is redistributed rather than destroyed—areas of destructive interference correspond to nearby zones of enhanced constructive interference.
Relationship between Interference and Coherence
For stable and observable interference, the two sources must be coherent. This ensures that their phase relationship remains constant over time, allowing fixed regions of constructive and destructive interference to persist.
Coherence: A property of two wave sources that maintain a constant phase relationship and identical frequency, enabling a steady interference pattern.
Without coherence, random phase variations cause fluctuating intensities, destroying the observable interference pattern.
In experiments, coherence is achieved by:
Splitting a single light source into two paths (as in Young’s double-slit experiment).
Using a single oscillator to drive two speakers for sound waves.
Employing one microwave generator for dual emission paths.
Visualising Interference Patterns
In two-source interference:
Constructive interference forms bright or high-intensity regions, where wave peaks align.
Destructive interference forms dark or low-intensity regions, where peaks meet troughs.
These alternate bands or fringes create the interference pattern.
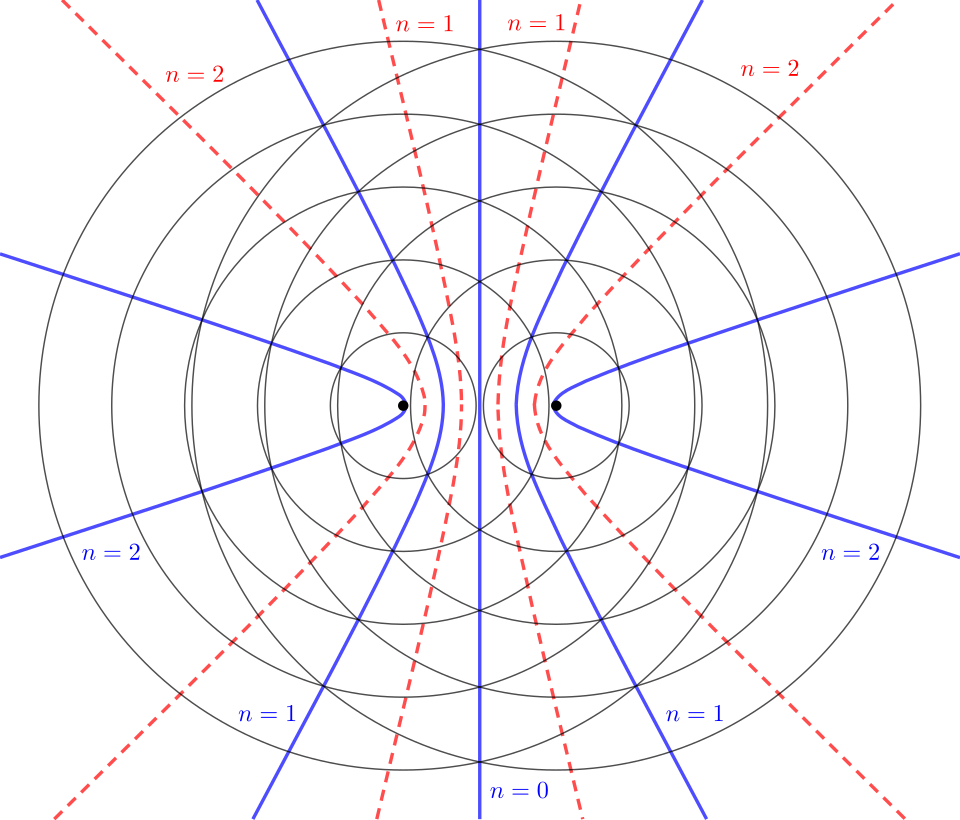
Two coherent point sources produce alternating antinodal (constructive) and nodal (destructive) lines. The hyperbolic geometry visualises where path difference equals nλ (bright) or (n+½)λ (dark). Labels are minimal and the layout is uncluttered. Source.
The spacing and clarity of the pattern depend on:
Wavelength (λ): longer wavelengths produce wider spacing between fringes.
Separation of sources (a): smaller separation increases fringe spacing.
Distance to the screen (D): greater distance spreads the pattern out.
These principles underlie the equations and setups in later subtopics, linking interference with experimental wavelength determination.
Intensity and Energy Distribution
The intensity of the resultant wave depends on the amplitude combination at each point. Since intensity is proportional to the square of amplitude, the interference pattern reflects the spatial variation in energy.
Constructive interference doubles amplitude, quadrupling intensity (since I ∝ A²).
Destructive interference reduces amplitude, potentially to zero intensity.
This redistribution of energy between bright and dark regions confirms that interference does not create or destroy energy—it simply relocates it.
Summary of Key Relationships
Constructive interference: Δx = nλ → waves in phase → maximum amplitude.
Destructive interference: Δx = (n + ½)λ → waves out of phase → minimum amplitude.
Coherence is required for stable interference.
Intensity patterns reveal the underlying wave behaviour of light, sound, and microwaves.
FAQ
When the amplitudes of two waves are unequal, complete cancellation does not occur even if they are perfectly out of phase.
The resultant amplitude equals the difference between the two amplitudes, and the wave that has greater amplitude dominates the residual motion.
In sound, this produces a quieter tone rather than silence. In light, it leads to reduced brightness instead of complete darkness.
If sources are not coherent, their phase relationship changes randomly over time, causing alternating constructive and destructive interference at unpredictable positions.
Because these variations occur too quickly for the eye or detector to resolve, the pattern averages out, and no stable fringes or interference bands remain visible.
Coherence is essential because it fixes the phase difference, allowing stationary bright and dark regions to persist.
Yes, in two- or three-dimensional interference patterns, different points within the same region can experience varying degrees of constructive or destructive interference.
For example:
Along an antinodal line, waves meet in phase (constructive).
Along an adjacent nodal line, waves meet out of phase (destructive).
These alternating lines coexist, forming the characteristic pattern of bright and dark fringes across a surface or field.
Phase difference determines how energy is distributed, not how much total energy exists.
In constructive interference, energy from both waves combines, producing a region of higher intensity.
In destructive interference, energy appears lost locally but is redistributed to nearby constructive regions.
Overall, the total energy remains constant, demonstrating conservation of energy even though local intensities vary.
Perfect cancellation requires:
Equal amplitudes
Perfectly opposite phase (180° difference)
Identical frequencies
In practice, slight mismatches in path length, amplitude, or frequency cause partial cancellation instead.
External factors such as vibrations, air currents, or imperfections in alignment can disturb the coherence and amplitude balance, resulting in residual light or sound where total darkness or silence was expected.
Practice Questions
Question 1 (2 marks)
Two sound waves of the same frequency meet at a point in space. The amplitude of the resultant sound is found to be zero.
Explain why this occurs, referring to the phase relationship between the waves.
Mark scheme:
1 mark: States that the two waves are out of phase by 180° (or π radians) / crest meets trough.
1 mark: Explains that destructive interference occurs, causing the displacements to cancel and the resultant amplitude to be zero.
Question 2 (5 marks)
Two coherent light sources, S1 and S2, produce an interference pattern on a distant screen. The light has a wavelength of 600 nm, and the separation between the sources is 1.2 mm.
At a point P on the screen, the path difference between light from S1 and S2 is 0.9 mm.
(a) State whether the interference at point P is constructive or destructive. (1 mark)
(b) Justify your answer with reference to the path difference and wavelength. (2 marks)
(c) Describe how the observed pattern would change if the wavelength of light were increased while keeping the slit separation constant. (2 marks)
Mark scheme:
(a)
1 mark: Constructive interference occurs.
(b)
1 mark: Calculates or explains that the path difference (0.9 mm) corresponds to 1.5 wavelengths (since 0.9 mm ÷ 0.0006 mm = 1.5).
1 mark: States that 1.5λ represents a phase difference of 270° (or 3π/2 radians), meaning waves are not in phase, therefore partial destructive interference occurs.
(Award 1 mark if candidate concludes destructive, not constructive, but shows consistent reasoning.)
(c)
1 mark: States that increasing wavelength increases fringe spacing (fringes move further apart).
1 mark: Explains this is because fringe separation is proportional to wavelength for fixed slit separation and distance to the screen.

