Stationary waves, also known as standing waves, form when two progressive waves of the same frequency and amplitude travel in opposite directions and interfere. They play a crucial role in understanding resonance, musical instruments, and wave behaviour in confined systems.

The Concept of Stationary Waves

When two identical waves moving in opposite directions overlap, their superposition creates regions of no displacement (nodes) and regions of maximum displacement (antinodes). The pattern formed appears to “stand still”, hence the name stationary wave.

Unlike progressive waves, stationary waves do not transfer energy along the medium. Instead, energy oscillates locally between kinetic and potential forms.

Conditions for Forming Stationary Waves

Stationary waves form under specific conditions:

• Two waves must have the same frequency, wavelength, and amplitude.

• The waves must travel in opposite directions along the same line.

• Reflection at a boundary is usually required to produce the counter-propagating wave.

• The medium must support resonance, such as a string or an air column fixed at certain points.

When these conditions are met, constructive and destructive interference create the stationary wave pattern.

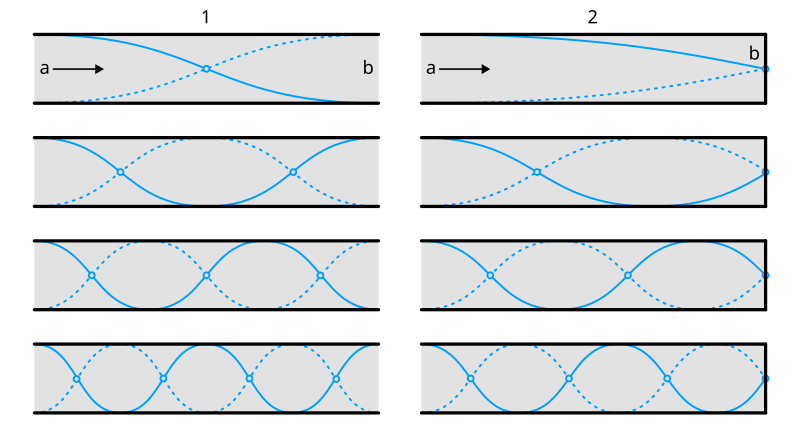
Stationary Waves on Stretched Strings

A stretched string fixed at both ends provides a classic example of stationary waves. When the string is plucked or driven by a vibration source, reflections at the fixed ends cause the incident and reflected waves to interfere.

At each fixed end, displacement must be zero, forming a node.

A labelled diagram of the first three standing-wave modes on a string of length L, fixed at both ends. Nodes occur at the ends (and evenly spaced along the string at higher modes), while antinodes mark maximum displacement. This directly illustrates how reflection and superposition create a stationary pattern on strings. Source.

Between nodes, the displacement varies, creating antinodes where oscillation amplitude is maximum.

The simplest mode of vibration is the fundamental mode or first harmonic, where there is one antinode between two nodes. Higher harmonics occur when additional nodes and antinodes form along the string.

EQUATION
—-----------------------------------------------------------------
Wave Speed (v) = fλ
v = wave speed (m s⁻¹)
f = frequency (Hz)
λ = wavelength (m)
—-----------------------------------------------------------------

For a string of length L, the fundamental wavelength is twice the string length (λ = 2L). Higher harmonics have wavelengths λ = 2L/n, where n is the harmonic number (1, 2, 3, …).

The frequency depends on the tension (T) and mass per unit length (μ) of the string:

EQUATION
—-----------------------------------------------------------------
Frequency of vibration (f) = (1/2L) × √(T/μ)
L = length of vibrating string (m)
T = tension in the string (N)
μ = mass per unit length (kg m⁻¹)
—-----------------------------------------------------------------

This relationship shows that higher tension or lower mass per unit length increases the frequency, producing higher-pitched tones.

Stationary Waves in Air Columns

Air columns within tubes can also support stationary waves when driven by sound sources such as tuning forks or loudspeakers. The wave reflects at the ends of the tube, creating interference between incident and reflected sound waves.

Two primary types of air columns exist:

• Open tubes: Both ends open to the air.

• Closed tubes: One end closed, one end open.

In open tubes, antinodes form at both open ends, since the air is free to move, while nodes occur within the tube.

A comparative diagram of standing waves in open and closed tubes, showing fixed node/antinode conditions at the ends. The patterns illustrate why the fundamental in an open tube has λ = 2L, while a closed tube’s fundamental has λ = 4L. Extra detail: higher harmonics are shown for clarity, which slightly exceeds the immediate syllabus focus. Source.

For an open tube of length L, the fundamental mode corresponds to half a wavelength fitting into the tube (λ = 2L). For a closed tube, the fundamental mode fits a quarter wavelength (λ = 4L).

Higher harmonics occur when additional nodes and antinodes fit within the same tube length, following predictable ratios of wavelength and frequency.

Stationary Waves with Microwaves

Stationary waves can also be formed using microwaves in laboratory experiments. A microwave transmitter emits waves towards a reflecting metal plate. The incident and reflected waves interfere to form a stationary pattern of nodes and antinodes.

A microwave detector probe can move through the field to detect points of maximum and minimum intensity:

• Antinodes correspond to points of maximum signal (constructive interference).

• Nodes correspond to points of zero signal (destructive interference).

The distance between adjacent nodes is half the wavelength (λ/2) of the microwaves.

This experimental method allows accurate measurement of microwave wavelengths.

Understanding Nodes and Antinodes

The fixed spacing between nodes and antinodes represents half the wavelength, a key characteristic of stationary waves across different systems.

Energy Distribution in Stationary Waves

In a stationary wave, energy is not transmitted through the medium as in a progressive wave. Instead, the energy oscillates between kinetic and potential forms within each segment:

• At nodes, potential energy is maximum and kinetic energy is zero.

• At antinodes, kinetic energy is maximum and potential energy is zero.

This energy exchange repeats rhythmically without net energy flow across the medium.

Experimental Production of Stationary Waves

To produce stationary waves, the following steps can be used for each medium:

Stretched String

• Attach one end of the string to a vibration generator.

• Adjust the frequency of the signal until resonance occurs and a stationary pattern forms.

• Observe nodes and antinodes along the string.

Air Column

• Use a tube with one or both ends open.

• Drive sound waves into the tube using a tuning fork or loudspeaker.

• Adjust the frequency or length of the column to locate resonance positions.

Microwaves

• Direct microwaves toward a metal reflector.

• Move a receiver along the path to detect alternating maxima and minima of intensity.

• Determine the wavelength using the spacing between nodes.

Stationary waves thus represent a fundamental principle of wave physics, providing the basis for resonance phenomena in strings, air columns, and electromagnetic systems. Their formation through superposition and reflection demonstrates the deep connection between wave behaviour, frequency, and boundary conditions.