OCR Specification focus:
‘Define work function and threshold frequency; explain their roles in emission.’
Understanding the work function and threshold frequency is essential to explaining the photoelectric effect, where light causes electrons to be emitted from a material’s surface. These concepts reveal how energy transfer in quantum processes operates at the atomic level.
The Role of Energy in Photoelectric Emission
When light strikes a metal surface, its energy is carried by photons. Each photon has a discrete energy given by E = hf, where h is Planck’s constant and f is the frequency of the radiation. For an electron to be emitted, this photon energy must overcome the energy binding the electron to the metal surface. This minimum required energy is the work function.
Work Function
The work function represents the minimum energy necessary for an electron to escape the surface of a material. It depends on the metal’s atomic structure and surface condition.
Work Function (Φ): The minimum energy required to remove an electron from the surface of a material.
Metals with lower work functions emit electrons more easily, while those with higher values require more energetic photons. For example, alkali metals such as sodium have low work functions, whereas transition metals such as nickel have higher ones. This explains why different materials respond differently to the same incident light.
Threshold Frequency
Because a photon’s energy depends on its frequency, a specific threshold frequency exists for each material — the lowest frequency of light capable of causing electron emission.
Threshold Frequency (f₀): The minimum frequency of electromagnetic radiation that can cause electron emission from a material’s surface.
Light below this frequency, no matter how intense, cannot eject electrons because the individual photons lack sufficient energy to overcome the material’s work function.
Schematic of the photoelectric effect: incident photons strike a solid and emit electrons from the surface. It supports the notion that emission occurs only if photon energy ≥ work function. The graphic is intentionally minimal, with labels focused on the process rather than broader semiconductor details. Source.
Relationship Between Work Function and Threshold Frequency
These two quantities are directly linked by Planck’s relation. When a photon just supplies enough energy to liberate an electron (without giving it any kinetic energy), the relationship can be expressed mathematically as:
EQUATION
—-----------------------------------------------------------------
Work Function (Φ) = h f₀
Φ = Work function (J)
h = Planck’s constant (6.63 × 10⁻³⁴ J·s)
f₀ = Threshold frequency (Hz)
—-----------------------------------------------------------------
This equation highlights the quantised nature of light energy and shows that emission occurs only when photons meet or exceed this frequency-energy requirement. The simplicity of this relationship provides one of the strongest pieces of evidence for the quantum model of light.
A material with a larger work function demands a higher threshold frequency.
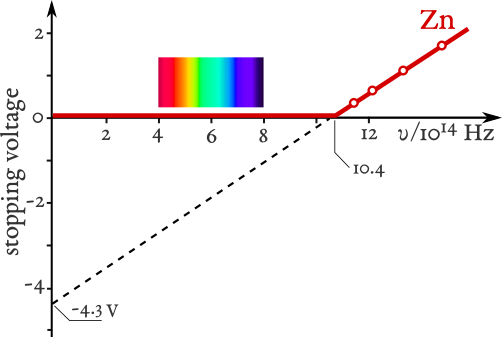
Linear plot of stopping potential (and thus KmaxK_{\text{max}}Kmax) versus frequency. The x-intercept marks the threshold frequency f0f_0f0 at which electrons just escape, so Φ=hf0\Phi=hf_0Φ=hf0. Above f0f_0f0, slope = h/e and the vertical intercept gives –Φ/e. Source.
Photon Energy and Emission Process
When light with frequency above the threshold frequency shines on a metal surface, electrons can absorb photons and gain energy. The process occurs in distinct steps:
Photon absorption: Each photon interacts with a single surface electron.
Energy transfer: The photon’s energy (hf) is transferred to the electron.
Emission: If hf ≥ Φ, the electron is emitted with maximum kinetic energy (KEₘₐₓ) equal to hf – Φ.
No emission: If hf < Φ, the electron remains bound within the material, regardless of light intensity.
This one-to-one photon–electron interaction distinguishes quantum behaviour from classical predictions, which incorrectly suggested that energy from intense light should eventually cause emission, regardless of frequency.
Energy Units and Interpretation
In photoelectric studies, energy values are often expressed in electronvolts (eV) for convenience.
Electronvolt (eV): The energy gained by an electron when accelerated through a potential difference of one volt.
Using electronvolts allows easier comparison between photon energies (typically a few eV) and work functions of metals, which often range between 2 eV and 5 eV.
The threshold frequency can therefore also be written in terms of photon wavelength using c = fλ, giving Φ = hc/λ₀, where λ₀ is the threshold wavelength corresponding to the lowest-energy photons that can cause emission.
Factors Affecting Work Function
The numerical value of the work function depends on both intrinsic and extrinsic factors:
Intrinsic Factors
Atomic structure: Metals with loosely bound outer electrons (e.g. potassium) have lower Φ.
Surface electron density: Denser electron clouds can raise Φ due to stronger attraction to the lattice.
Extrinsic Factors
Surface contamination or oxidation: Deposits or oxides can increase Φ by changing surface bonding.
Temperature: Elevated temperatures can slightly reduce Φ as lattice vibrations weaken electron binding.
Crystalline orientation: In single crystals, different faces of the same material can exhibit slightly different work functions.
Importance in Quantum Theory
The relationship between work function and threshold frequency was critical evidence supporting the quantum theory of light. Classical wave theory predicted that increasing light intensity should eventually eject electrons, but experiments showed emission only occurred when light exceeded a specific frequency. This contradiction could only be explained if light energy came in discrete packets — photons — each carrying quantised energy hf.
This understanding led Albert Einstein to propose his photoelectric equation, connecting photon energy, work function, and the kinetic energy of emitted electrons. It earned him the Nobel Prize in 1921 and solidified the concept that electromagnetic radiation exhibits both wave-like and particle-like behaviour.
Summary of Key Relationships
For clarity, the essential interconnections are as follows:
Photon energy: E = hf
Work function–threshold link: Φ = hf₀
Condition for emission: hf ≥ Φ
Kinetic energy of emitted electrons: KEₘₐₓ = hf – Φ
These relations define the quantum boundary between photon energy sufficient for emission and energy that is absorbed without freeing an electron.
Conceptual Understanding
Students should appreciate that:
The work function is a property of the material, not of the incident light.
The threshold frequency corresponds precisely to this work function through Planck’s constant.
No amount of low-frequency light can cause emission, illustrating that energy transfer is quantised.
The photoelectric effect was one of the first phenomena demonstrating the particle nature of light, bridging classical electromagnetism and modern quantum physics.
FAQ
The work function depends on how strongly electrons are bound to the metal’s surface atoms.
Metals with loosely held outer electrons, such as alkali metals, have lower work functions because less energy is needed to release an electron. Transition metals and those with tightly packed atomic structures tend to have higher work functions.
Surface conditions also influence this value — oxidation, contamination, or crystal orientation can all alter how easily electrons can escape.
The threshold frequency represents the minimum photon energy that can overcome the binding energy holding electrons to a metal’s surface.
Below this frequency, photons do not have enough energy to eject electrons, regardless of light intensity. Above it, the photon energy exceeds the work function, and the excess becomes the kinetic energy of the emitted electron.
It defines the boundary between no emission and observable photoelectric emission.
Yes. The work function is sensitive to the metal’s surface properties.
Oxidation or contamination increases it by adding energy barriers for electron escape.
Heating can decrease it slightly as lattice vibrations weaken electron binding.
Surface cleaning or polishing often lowers it by removing impurities.
In precision experiments, surfaces are kept clean and in vacuum to maintain a stable, known work function.
The threshold frequency depends only on the energy of individual photons (E = hf), not on how many photons arrive per second.
Increasing intensity increases the number of photons, but if each photon’s frequency is below the threshold, none have sufficient energy to liberate electrons.
Thus, photon energy — determined solely by frequency — governs emission, not total light intensity.
Yes. The work function can be thought of as the energy difference between the Fermi level (the highest occupied electron energy at absolute zero) and the vacuum level (energy required to remove an electron completely from the surface).
This relationship links the macroscopic photoelectric behaviour to the microscopic electronic structure of the material, making the work function a crucial parameter in surface physics and electronic device design.
Practice Questions
Question 1 (2 marks)
A metal surface has a work function of 3.2 eV.
State what is meant by the term work function and explain what happens when light of frequency lower than the threshold frequency is incident on this surface.
Question 1 (2 marks)
1 mark: Defines work function as the minimum energy required to remove an electron from the surface of a material.
1 mark: States that if light has a frequency below the threshold frequency, no electrons are emitted because photon energy is insufficient to overcome the work function.
Question 2 (5 marks)
A metal has a threshold frequency of 6.0 × 10¹⁴ Hz.
(a) Calculate the work function of the metal in joules.
(b) Calculate the maximum kinetic energy of the emitted electrons when the surface is illuminated with light of frequency 8.5 × 10¹⁴ Hz.
(c) Explain why increasing the intensity of the light at this frequency increases the rate of emission of electrons but not their maximum kinetic energy.
(Take Planck’s constant h = 6.63 × 10⁻³⁴ J·s)
Question 2 (5 marks)
(a) (2 marks)
1 mark: Correct use of Φ = h f₀.
1 mark: Substitutes values and obtains Φ = (6.63 × 10⁻³⁴) × (6.0 × 10¹⁴) = 3.98 × 10⁻¹⁹ J.
(b) (1 mark)
1 mark: Uses KEmax = hf – Φ and substitutes f = 8.5 × 10¹⁴ Hz to give KEmax = (6.63 × 10⁻³⁴ × 8.5 × 10¹⁴) – 3.98 × 10⁻¹⁹ = 1.65 × 10⁻¹⁹ J.
(c) (2 marks)
1 mark: States that increasing intensity means more photons per second, leading to a greater rate of electron emission.
1 mark: States that each photon’s energy (hf) isunchanged, so the maximum kinetic energy of emitted electrons remains the same.

