OCR Specification focus:
‘Electron diffraction experiments provide evidence for wave-like behaviour of particles.’
Electron diffraction reveals that particles such as electrons exhibit wave-like properties, providing direct experimental support for wave–particle duality — a cornerstone of modern quantum physics.
Understanding Electron Diffraction
Historical Context
Before quantum theory developed, light was considered purely a wave, and matter was believed to consist of particles. The discovery that electrons—traditionally seen as particles—can diffract like waves overturned this classical distinction. The electron diffraction experiment, first demonstrated by Davisson and Germer (1927), provided the crucial evidence confirming Louis de Broglie’s hypothesis that all matter has a wavelength dependent on its momentum.
Concept of Wave–Particle Duality
Wave–particle duality describes how particles sometimes behave as waves and vice versa. This experiment demonstrated that the boundary between waves and particles is not rigid but governed by quantum principles.
The Principle of Electron Diffraction
Wave Behaviour of Electrons
When a beam of electrons passes through a crystalline material—such as nickel or graphite—the regular atomic spacing acts like a diffraction grating. The electrons are scattered by the atoms in the crystal, and if their wavelength is comparable to the atomic spacing, they produce interference patterns identical to those produced by waves of light.
Electron Diffraction: The phenomenon where a beam of electrons, when incident on a crystalline material, produces a pattern of constructive and destructive interference due to the wave-like nature of electrons.
The de Broglie Wavelength
The experiment’s success depends on the de Broglie wavelength of electrons being of the same order of magnitude as the crystal’s atomic spacing, typically around 10⁻¹⁰ m.
EQUATION
—-----------------------------------------------------------------
de Broglie Wavelength (λ) = h / p
λ = Wavelength of the particle (m)
h = Planck’s constant (6.63 × 10⁻³⁴ J s)
p = Momentum of the particle (kg m s⁻¹)
—-----------------------------------------------------------------
When electrons are accelerated through a potential difference, their momentum depends on their velocity, which can be related to the accelerating voltage. Thus, varying the voltage changes the de Broglie wavelength, altering the diffraction pattern observed.
The Davisson–Germer Experiment
Experimental Arrangement
The Davisson–Germer setup used a beam of electrons emitted from a heated filament and accelerated towards a nickel crystal target.

Schematic of the Davisson–Germer experiment showing a thermionic electron source, the single-crystal nickel target, and an angular detector for scattered intensity. Electrons scatter from regularly spaced atomic planes, producing diffraction maxima at specific angles. This geometry was crucial to demonstrating electrons’ wave-like behaviour. Source.
The electrons were scattered by the crystal and detected at various angles.
Key components included:
Electron source: Provided a steady stream of electrons.
Accelerating voltage: Controlled the electrons’ kinetic energy and wavelength.
Nickel crystal: Acted as a diffraction grating due to its regular atomic structure.
Detector: Measured the intensity of scattered electrons as a function of angle.
Observations
At certain accelerating voltages, the detector recorded distinct peaks in intensity, indicating that electrons were constructively interfering—a hallmark of diffraction. The measured angles of these peaks corresponded precisely to those predicted by Bragg’s law, which governs diffraction of waves by crystal planes.
EQUATION
—-----------------------------------------------------------------
Bragg’s Law: nλ = 2d sin θ
n = Order of diffraction (integer)
λ = Wavelength of incident wave (m)
d = Spacing between atomic planes in the crystal (m)
θ = Angle of reflection/diffraction (degrees or radians)
—-----------------------------------------------------------------
This relationship, long used for X-ray diffraction, confirmed that electrons behaved exactly as if they were waves with wavelength λ = h/p.
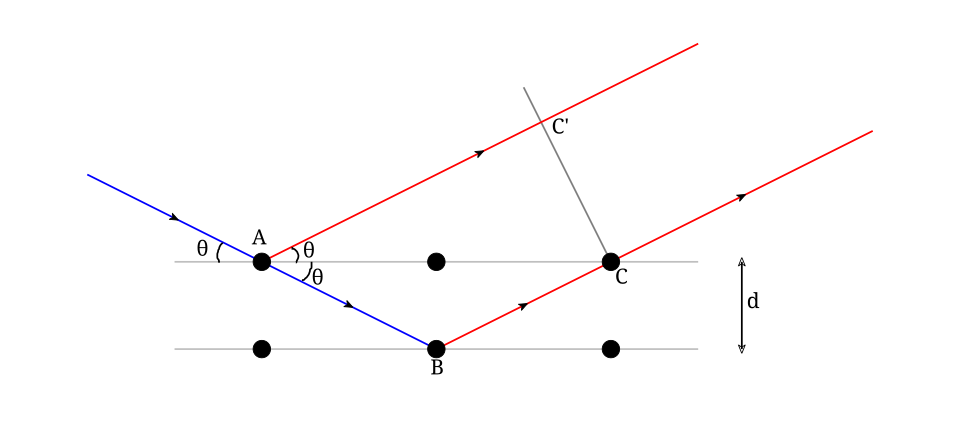
Diagram illustrating Bragg’s law, showing incident and reflected wavefronts from parallel crystal planes separated by distance d, with θ measured to the planes. Constructive interference occurs when path difference equals nλ. The schematic directly links the observed diffraction angles to the electron wavelength. Source.
Interpreting the Evidence
Wave–Like Properties of Matter
The electron diffraction pattern is direct evidence that electrons possess wave-like characteristics. The fact that the observed diffraction maxima matched theoretical predictions for wave interference proved that electrons cannot be described purely as particles.
Key observations included:
Interference maxima and minima identical to those for light or X-rays.
Dependence on wavelength, changing predictably with electron energy.
Loss of pattern at high energies, when wavelengths become too small relative to atomic spacing.
Dependence on Accelerating Voltage
When the accelerating voltage increases, electron speed and momentum increase, which decreases their de Broglie wavelength. Consequently:
Diffraction fringes move closer together.
For very high voltages (small λ), the diffraction pattern disappears.
This confirms that observable diffraction only occurs when λ is comparable to atomic spacing.
Significance and Implications
Validation of de Broglie’s Hypothesis
The experiment verified Louis de Broglie’s 1924 proposal that all matter exhibits both wave and particle properties. De Broglie’s idea had been speculative until the Davisson–Germer results confirmed it experimentally. The success of this hypothesis laid the groundwork for quantum mechanics, particularly the development of the Schrödinger wave equation, which treats particles as wavefunctions.
Relation to the Quantum Model
Electron diffraction demonstrates that quantum behaviour dominates at small scales. For macroscopic objects with large momentum, the de Broglie wavelength is extremely small, and wave effects become unobservable. However, for microscopic particles like electrons, protons, or neutrons, the wavelength can be significant enough to observe diffraction and interference, showing that quantum effects are inherently scale-dependent.
Broader Impact in Physics
Electron diffraction not only supports the conceptual shift toward quantum theory but also forms the basis of practical technologies, such as:
Electron microscopes, which exploit electron waves for high-resolution imaging.
Crystallography, where diffraction patterns reveal atomic structure.
Surface analysis techniques, such as Low-Energy Electron Diffraction (LEED).
These applications demonstrate how a fundamental quantum phenomenon directly informs modern experimental and applied physics.
Summary of Key Ideas
Electron diffraction provides concrete proof of the wave-like behaviour of matter.
de Broglie wavelength links momentum to wave properties.
Davisson–Germer experiment confirmed diffraction at atomic scales.
Bragg’s law accurately predicts observed diffraction peaks.
The results support the wave–particle duality central to quantum mechanics.
FAQ
Nickel was chosen because it can be prepared as a single crystal with well-defined atomic planes that act as a natural diffraction grating for electrons.
Its lattice spacing is comparable to the de Broglie wavelength of electrons accelerated by a few tens of volts, making diffraction effects clearly observable.
Additionally, nickel’s durability and ability to maintain a clean, ordered surface under vacuum conditions ensured consistent, reproducible diffraction patterns.
The angles of scattered electrons are measured using a rotatable detector or a fluorescent screen calibrated to show the angular position of intensity maxima.
The screen or detector is placed on an arc centred on the crystal.
Each spot or ring’s angular position corresponds to a particular diffraction order.
Calibration allows these angles to be related to known crystal plane spacings using Bragg’s law.
Precision in angle measurement is essential for determining electron wavelength and verifying the wave–particle duality.
At high accelerating voltages, electrons gain large momentum, causing their de Broglie wavelength to become extremely small.
When this wavelength is much smaller than the atomic spacing of the crystal, the conditions for diffraction and constructive interference are no longer satisfied.
As a result:
Diffraction rings merge or vanish.
The scattering pattern resembles that of classical particles rather than waves.
This illustrates that wave effects are only observable when the wavelength is comparable to atomic dimensions.
Both techniques use Bragg’s law and rely on interference from atomic planes, but the wave sources differ fundamentally.
X-rays are electromagnetic waves and interact with electron clouds around atoms.
Electrons are matter waves and are scattered by the electrostatic potential of atomic nuclei and inner electrons.
Electron diffraction typically produces patterns at lower energies and shorter distances, making it highly useful for studying surface structures and thin films.
To produce a sharp diffraction pattern, several key conditions must be maintained:
The experiment must occur in a high vacuum to prevent electrons scattering off air molecules.
The crystal surface must be clean and well-ordered to ensure coherent scattering.
The accelerating voltage should be stable to keep the electron wavelength consistent.
The electron beam must be narrow and well-collimated for high spatial coherence.
These conditions ensure that observed interference effects are due solely to diffraction by the crystal lattice.
Practice Questions
Question 1 (2 marks)
Explain how the observation of diffraction patterns in the Davisson–Germer experiment provides evidence for the wave-like nature of electrons.
Mark scheme:
1 mark: States that electrons produce an interference or diffraction pattern when scattered by a crystal.
1 mark: Explains that diffraction is a property of waves, so the pattern shows electrons behave as waves.
Question 2 (5 marks)
In an electron diffraction experiment, electrons are accelerated through a potential difference before striking a crystal.
(a) State the equation that relates the de Broglie wavelength of an electron to its momentum. (1 mark)
(b) Explain how changing the accelerating voltage affects the observed diffraction pattern. (4 marks)
Mark scheme:
(a)
1 mark: Correctly states λ = h / p
(b)
1 mark: States that increasing accelerating voltage increases electron speed (and therefore momentum).
1 mark: Explains that greater momentum decreases the de Broglie wavelength.
1 mark: States that smaller wavelength means diffraction fringes or rings move closer together or become less spread out.
1 mark: Recognises that at very high voltages (very small λ), diffraction may no longer be observable because λ becomes much smaller than atomic spacing.

