OCR Specification focus:
‘Electrons diffract through thin polycrystalline graphite; ring patterns relate to atomic spacing.’
Electrons display wave-like properties when diffracted by polycrystalline graphite, producing distinctive ring patterns. These patterns provide direct experimental evidence for the wave–particle duality of matter.
Electron Diffraction by Polycrystalline Graphite
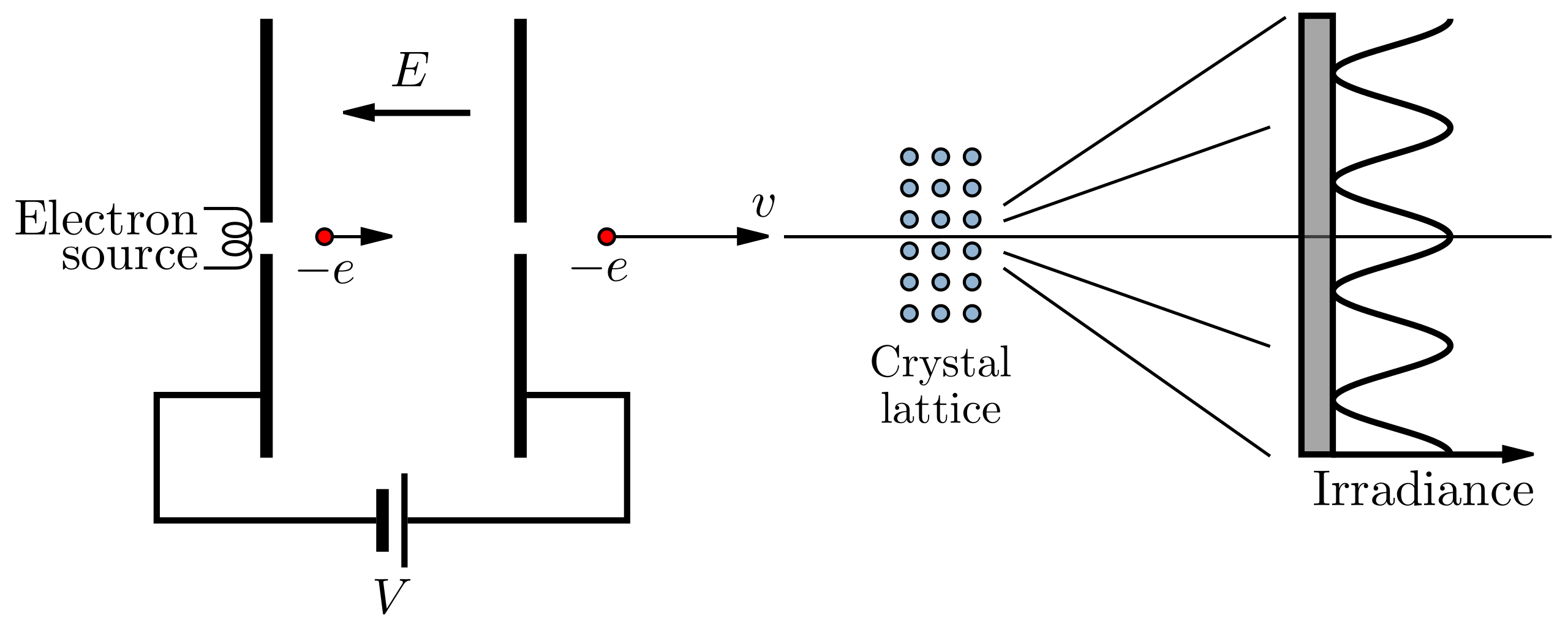
When a beam of electrons passes through a thin sheet of polycrystalline graphite, a diffraction pattern is observed on a fluorescent screen. This phenomenon confirms that electrons, though particles, exhibit wave behaviour under certain conditions. The diffraction arises due to the regular atomic arrangement within the graphite crystals, causing interference effects analogous to those seen with light waves.
Graphite is described as polycrystalline because it consists of many small, randomly oriented crystallites (tiny single crystals). Each crystallite diffracts electrons according to its crystal orientation, leading to circular diffraction rings rather than discrete spots.
The Concept of Electron Diffraction
Understanding Wave–Particle Duality
The concept that all matter exhibits both wave-like and particle-like behaviour was proposed by Louis de Broglie in 1924. His hypothesis suggests that every moving particle has an associated wavelength that determines its potential for diffraction or interference.
de Broglie Wavelength: The wavelength associated with a moving particle, given by the relationship λ = h/p, where h is Planck’s constant and p is the particle’s momentum.
In the context of electron diffraction, this means that a stream of electrons can behave similarly to waves of light when encountering atomic-scale structures.
Experimental Setup and Observation
Apparatus Overview
A typical electron diffraction experiment employs a cathode ray tube (CRT) containing:
Schematic of an electron diffraction tube showing the electron gun, thin crystalline target (e.g. polycrystalline graphite), and fluorescent screen. The setup produces a ring pattern when the de Broglie wavelength of the electrons satisfies the Bragg condition for lattice planes in the graphite. Labels are minimal and the layout matches the apparatus list in the notes; the diagram is generic rather than graphite-specific, which is acceptable for apparatus context. Source.
An electron gun, which accelerates electrons through a known potential difference.
A thin polycrystalline graphite target, often only a few nanometres thick.
A fluorescent screen to display the resulting diffraction pattern.
When the accelerated electrons strike the graphite target, they interact with the atoms in its crystalline lattice planes. The regular spacing between these planes acts as a diffraction grating for the electron waves.
As electrons pass through the crystal, they are diffracted at specific angles determined by their wavelength and the atomic spacing. On the screen, this produces concentric bright rings — a pattern characteristic of diffraction by randomly oriented crystallites.

Concentric diffraction rings formed by electrons passing through a thin polycrystalline graphite foil. The central bright spot is the transmitted beam, while successive rings correspond to different lattice plane spacings that satisfy Bragg’s law. Minor background glow and intensity variations are normal for school-lab tubes and do not affect interpretation. Source.
Relationship Between Electron Energy, Wavelength, and Diffraction Pattern
The wavelength of electrons is inversely proportional to their momentum, which depends on their kinetic energy gained through acceleration.
EQUATION
—-----------------------------------------------------------------
de Broglie Relationship (λ) = h / p
λ = h / √(2meV)
λ = Electron wavelength (metres)
h = Planck’s constant (6.63 × 10⁻³⁴ J·s)
m = Electron mass (9.11 × 10⁻³¹ kg)
e = Electron charge (1.60 × 10⁻¹⁹ C)
V = Accelerating potential (volts)
—-----------------------------------------------------------------
Increasing the accelerating voltage increases the electrons’ momentum and reduces their wavelength. Consequently, the diffraction ring radius decreases, as shorter wavelengths diffract at smaller angles.
The diffraction condition for constructive interference follows the same principle as Bragg’s law used in X-ray diffraction.
EQUATION
—-----------------------------------------------------------------
Bragg’s Law: nλ = 2d sinθ
n = Order of diffraction (integer)
λ = Wavelength of electrons (metres)
d = Interplanar spacing in the crystal (metres)
θ = Angle of diffraction (radians)
—-----------------------------------------------------------------
These relationships link the observed ring diameters to the interatomic spacing (d) within graphite, providing a powerful method for determining crystal structure.
Origin of the Diffraction Rings
Because graphite is polycrystalline, its microscopic crystallites are randomly oriented. Each orientation satisfies Bragg’s condition for a different subset of lattice planes. As a result, instead of discrete diffraction spots (as seen for single crystals), the overlapping diffraction from numerous orientations produces rings of constructive interference.
Key observations include:
Central bright spot: Undiffracted electrons passing straight through.
Concentric bright rings: First, second, and higher-order diffraction corresponding to multiple sets of lattice planes.
Intensity variation: Outer rings are typically fainter due to reduced electron beam intensity and increased scattering angles.
The radius of each ring is directly related to the Bragg angle (θ) and the interplanar spacing (d) in the graphite.
Significance of the Graphite Diffraction Experiment
This experiment was historically crucial in confirming that electrons exhibit wave behaviour. When first performed by Davisson and Germer (1927) and later by Thomson (1928), it provided direct experimental evidence for the de Broglie hypothesis. It showed that particles of matter can diffract and interfere — phenomena previously thought exclusive to waves.
The results demonstrated:
The wavelength of electrons depends on their momentum.
The observed ring diameters agree precisely with values predicted from known graphite lattice spacings.
Electron diffraction is consistent with quantum mechanics, reinforcing the model of wave–particle duality.
Interpretation and Analytical Use
By measuring the diameters of diffraction rings at various accelerating voltages, one can calculate the wavelength of electrons and determine interplanar spacings within graphite.
This process involves:
Measuring the ring radius (r) on the fluorescent screen.
Knowing the camera length (L), i.e. distance between the target and the screen.
Using the geometry to relate sinθ ≈ r/L for small angles.
Combining this with Bragg’s law enables calculation of d-spacing values, which typically correspond to the graphite’s (002), (100), and (110) lattice planes.
These measurements match those obtained through X-ray diffraction, demonstrating that both light and electrons reveal crystal structures through their wave nature.
Broader Quantum Context
Electron diffraction by polycrystalline graphite exemplifies the quantum mechanical principle that particles can behave as waves under certain conditions. The de Broglie wavelength is significant when it is comparable to the atomic spacing within materials (around 10⁻¹⁰ m). For electrons accelerated through typical voltages (a few kilovolts), the wavelength falls within this range, making diffraction observable.
At higher particle energies or for larger objects, the wavelength becomes exceedingly small, and wave behaviour becomes negligible — hence, diffraction is not observable for macroscopic bodies. This illustrates the scale-dependent nature of quantum phenomena.
In conclusion, diffraction by polycrystalline graphite provides compelling visual and quantitative evidence for the wave properties of electrons. The resulting diffraction rings directly relate to atomic spacings within the material and stand as a cornerstone experiment supporting the wave–particle duality central to quantum physics.
FAQ
Polycrystalline graphite is used because it contains many small crystallites randomly oriented in different directions. This ensures that all possible crystal orientations are present, allowing diffraction to occur at many angles simultaneously.
As a result, instead of producing sharp diffraction spots like a single crystal, the overlapping patterns from each orientation form concentric diffraction rings. This makes the phenomenon much easier to observe and measure in a standard laboratory setup.
The accelerating voltage determines the kinetic energy and wavelength of the electrons.
Increasing voltage → higher energy → shorter wavelength → rings move closer together and decrease in radius.
Decreasing voltage → lower energy → longer wavelength → rings move further apart and increase in radius.
This relationship provides a clear visual way to confirm that electron wavelength varies inversely with momentum, consistent with the de Broglie equation.
If the graphite foil were too thick, electrons would undergo multiple scattering events before emerging.
This would cause:
Loss of coherence in the electron waves.
Blurring or disappearance of the diffraction rings.
Increased absorption of electrons, reducing image brightness.
Therefore, the foil must be only a few nanometres thick to allow electrons to pass through with minimal disturbance and preserve clear diffraction patterns.
Yes. Materials such as polycrystalline aluminium, gold, or nickel can also be used. The choice depends on:
The ability to produce a very thin, uniform foil.
The material’s atomic spacing being comparable to the electron wavelength at accessible voltages.
Sufficient electron transparency to produce measurable diffraction.
Graphite remains popular because it is easy to prepare in thin layers, chemically stable, and has well-defined crystalline planes suitable for educational and research demonstrations.
Diffraction is a purely wave phenomenon, arising from the interference of coherent waves passing through a regular structure.
When electrons—known to be particles—produce diffraction rings, it shows they must also possess wave-like properties. The measured wavelengths from the ring patterns match those predicted by λ = h/p, confirming that electrons behave according to quantum wave–particle duality.
This experiment thus provides direct, visible proof that matter can exhibit both particle and wave characteristics, depending on how it is observed.
Practice Questions
Question 1 (2 marks)
When a beam of electrons is directed at a thin sheet of polycrystalline graphite, a pattern of concentric bright rings appears on a fluorescent screen.
Explain why rings are produced rather than discrete spots.
Mark Scheme
(1 mark) Graphite consists of many tiny crystals (crystallites) that are randomly oriented.
(1 mark) Each crystal diffracts electrons in different directions, producing rings when all orientations are combined.
Question 2 (5 marks)
In an electron diffraction experiment, electrons are accelerated through a known potential difference and then directed at a thin sheet of polycrystalline graphite.
(a) State the equation linking the wavelength of the electrons with the accelerating potential. (1 mark)
(b) Explain how the observed diffraction pattern can be used to determine the spacing between atomic planes in graphite. (4 marks)
Mark Scheme
(a)
(1 mark) Correct equation: λ = h / √(2meV)
(b)
(1 mark) The radius of each diffraction ring on the screen corresponds to a specific diffraction angle θ.
(1 mark) Using the geometry of the setup, sinθ ≈ r / L (for small angles), where r is ring radius and L is the camera length.
(1 mark) Bragg’s law (nλ = 2d sinθ) is applied to relate the wavelength to the interplanar spacing d.
(1 mark) Substituting the known accelerating voltage (and hence λ) and measured θ gives the value of d, allowing determination of the atomic spacing in graphite.

