OCR Specification focus:
‘Diffraction observable when de Broglie wavelength is comparable to inter-atomic spacing.’
Conditions for Observable Diffraction
The diffraction of particles such as electrons reveals their wave-like behaviour. For diffraction to be observable, the de Broglie wavelength of the particles must be of a similar scale to the structural features they encounter, such as inter-atomic spacings in a crystal lattice. This subtopic explores the physical conditions required for wave-particle duality to produce measurable diffraction effects.
The Concept of Particle Diffraction
When a stream of particles passes through a regularly spaced structure (for example, atoms in a crystal), it can produce a diffraction pattern similar to that observed when light waves pass through slits or gratings. The wave-particle duality principle means that matter exhibits both particle and wave characteristics depending on the experimental setup.
Diffraction: The spreading and interference of waves when they encounter an obstacle or pass through a gap comparable in size to their wavelength.
This effect demonstrates that even particles with mass, such as electrons, neutrons, or atoms, can behave as waves under suitable conditions.
The de Broglie Wavelength and Its Significance
The idea of a matter wave was first proposed by Louis de Broglie, who associated a wavelength with all moving particles. The de Broglie relation links a particle’s momentum to its wavelength.
EQUATION
—-----------------------------------------------------------------
de Broglie Wavelength (λ) = h / p
λ = wavelength of the particle (m)
h = Planck’s constant (6.63 × 10⁻³⁴ J·s)
p = momentum of the particle (kg·m·s⁻¹)
—-----------------------------------------------------------------
A particle’s momentum depends on both its mass and velocity, meaning that lighter and slower particles have longer wavelengths. To observe diffraction, the wavelength must not be negligible compared to the dimensions of the structure interacting with the particle beam.
Inter-Atomic Spacing and the Diffraction Condition
The inter-atomic spacing in solids typically lies between 0.1 nm and 0.3 nm (10⁻¹⁰ m). For observable diffraction, the de Broglie wavelength must be of the same order of magnitude. If the wavelength is much smaller or larger than this spacing, clear diffraction patterns will not form.
Inter-atomic spacing: The average distance between the nuclei of neighbouring atoms in a crystalline lattice, usually around 10⁻¹⁰ m.
When electrons have suitable kinetic energies, their de Broglie wavelength becomes comparable to these atomic separations, resulting in the ring diffraction patterns seen in experiments such as electron diffraction through thin polycrystalline graphite.

Electron diffraction rings formed by a low-energy electron beam passing through polycrystalline graphite. Each ring corresponds to constructive interference from lattice planes with specific inter-planar spacing. The clarity of the rings reflects λ being of the same order as the atomic spacing. Source.
Why Comparable Wavelengths Are Required
Diffraction arises due to interference between waves scattered from different points within the structure. For constructive and destructive interference to occur coherently:
The path difference between scattered waves must be an integer multiple of the wavelength.
The scattering centres (atoms, ions, or molecules) must be regularly spaced and fixed in position.
The wavelength must be comparable to or larger than the structural spacing to allow overlapping wavefronts.
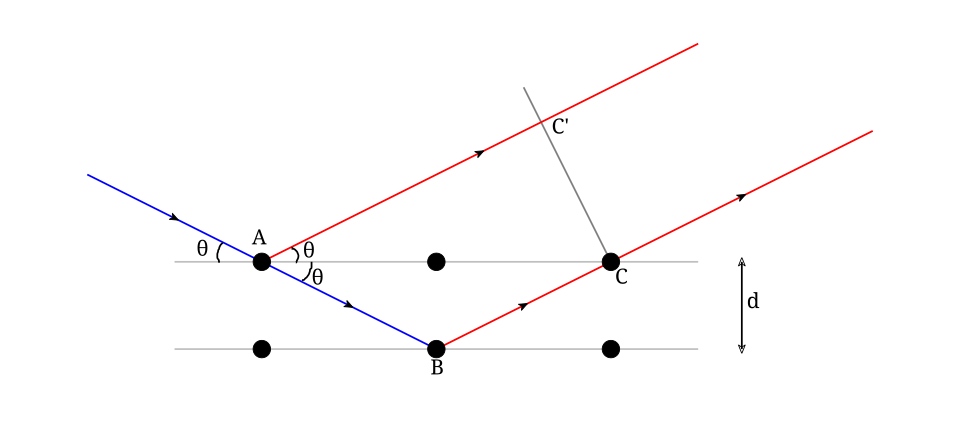
Schematic of Bragg’s law showing incident and reflected beams from parallel crystal planes separated by spacing d, with angle θ and path-difference 2d sin θ. Constructive interference occurs when nλ = 2d sin θ. This condition links wavelength to lattice spacing, explaining when diffraction patterns appear. Source.
If the wavelength is too short compared to the inter-atomic distance, the wavefronts pass through without noticeable interference, and the diffraction pattern becomes indistinguishable from direct transmission. Conversely, if the wavelength is too long, diffraction effects smear out, and no sharp pattern appears.
Adjusting Experimental Conditions
To achieve the correct wavelength range for diffraction, experimental parameters can be controlled:
Particle type: Electrons, neutrons, and atoms are commonly used; each has different mass and energy characteristics.
Particle energy: By altering the accelerating potential (for charged particles like electrons), one can adjust momentum and therefore wavelength.
Material choice: Crystalline solids with known lattice spacings, such as graphite or nickel, provide regular atomic structures that act as natural diffraction gratings.
EQUATION
—-----------------------------------------------------------------
Kinetic Energy Relation (for electrons):
E = eV = ½mv²
E = kinetic energy gained by charge e through potential difference V (J)
m = mass of the electron (kg)
v = velocity of the electron (m·s⁻¹)
—-----------------------------------------------------------------
Combining this with the de Broglie equation gives a way to link the accelerating voltage directly to the electron wavelength. Increasing the accelerating voltage increases momentum, shortening the wavelength and reducing diffraction visibility.
Practical Examples of Observable Diffraction
Electron diffraction provides the most direct evidence of this condition. When low-energy electrons (typically accelerated by 2–10 kV) pass through a thin layer of graphite:
The electrons interact with many lattice planes.
The resulting scattered waves interfere to form circular diffraction rings on a fluorescent screen.
The radii of these rings depend on the wavelength, confirming that matter behaves as a wave when λ ≈ inter-atomic spacing.
For neutrons or atoms, their de Broglie wavelengths can be adjusted through their temperature (velocity). Slow neutrons with wavelengths around 0.1 nm can be diffracted by crystals in the same way as X-rays.
Limitations and Macroscopic Inapplicability
While the de Broglie wavelength exists for all matter, it becomes extremely small for macroscopic objects. For instance, a moving baseball has a wavelength many orders of magnitude smaller than atomic dimensions, making diffraction impossible to detect. Thus, observable diffraction is limited to microscopic particles such as electrons, neutrons, atoms, and molecules.
The essential requirement remains that the particle’s wavelength must be comparable to the dimensions of the diffracting structure. Only under this condition can wave-like interference occur, producing measurable diffraction patterns and confirming the wave nature of matter.
FAQ
Polycrystalline materials consist of many tiny crystals, or grains, each oriented randomly. When an electron beam interacts with the regularly spaced atoms within these grains, diffraction occurs in many directions simultaneously.
Because all possible crystal orientations are present, the diffracted beams form concentric rings rather than discrete spots, which are characteristic of single-crystal diffraction. The radii of these rings correspond to specific inter-atomic spacings in the crystal structure.
Increasing the accelerating voltage gives the electrons more kinetic energy, increasing their momentum and reducing their de Broglie wavelength.
A shorter wavelength means smaller diffraction angles, so the rings move closer together.
A lower voltage gives a longer wavelength, leading to wider spacing between the rings.
Thus, adjusting voltage allows experimental control over the diffraction pattern and confirms the relationship between energy, momentum, and wavelength.
Blurring often arises when the experimental conditions deviate from ideal requirements. Key factors include:
Non-uniform crystal thickness or amorphous samples that scatter electrons irregularly.
High electron energies, giving wavelengths much smaller than atomic spacings, leading to minimal diffraction.
Poor vacuum conditions or contamination, which scatter the beam before it reaches the target.
Thermal vibrations of atoms, which disrupt regular spacing and weaken interference effects.
Precise control of these variables is essential for sharp diffraction patterns.
Yes. Any particle with a measurable de Broglie wavelength comparable to inter-atomic spacings can exhibit diffraction, provided it interacts coherently with the material’s structure.
Common examples include:
Neutrons, which penetrate deeply into materials and reveal atomic positions, particularly of light atoms.
Atoms or molecules, observed in molecular beam diffraction experiments under ultra-cold conditions.
However, heavier particles require very low velocities to achieve suitable wavelengths, which limits experimental practicality.
By measuring the radii of diffraction rings and knowing the wavelength of the particles, the atomic spacing can be calculated using the relationship between path difference and interference conditions.
In electron diffraction, this is often based on Bragg’s law (nλ = 2d sin θ). The measurable quantities are:
λ, derived from the accelerating voltage of the electrons.
θ, obtained from the geometry of the ring pattern.
Using these, the inter-atomic spacing d can be estimated with high accuracy, allowing detailed study of crystalline materials.
Practice Questions
Question 1 (2 marks)
Explain why diffraction of electrons is only observable when the de Broglie wavelength of the electrons is comparable to the spacing between atoms in a crystal.
Mark Scheme:
1 mark: States that diffraction occurs when the wavelength is similar in size to the atomic spacing or dimensions of the diffracting structure.
1 mark: Explains that if the wavelength is much smaller or larger, interference between scattered waves does not produce an observable diffraction pattern.
Question 2 (5 marks)
A beam of electrons is directed at a thin layer of polycrystalline graphite. Explain how the appearance of a ring diffraction pattern on a fluorescent screen provides evidence for the wave nature of electrons. Include in your answer the conditions necessary for this diffraction to be observed.
Mark Scheme:
1 mark: Mentions that the electrons act as waves and undergo diffraction when passing through the regular arrangement of atoms in the graphite crystal.
1 mark: States that constructive interference between scattered waves produces concentric diffraction rings.
1 mark: Notes that the pattern depends on the de Broglie wavelength of the electrons, which is related to their momentum.
1 mark: States that diffraction is only observable when the de Broglie wavelength is comparable to the inter-atomic spacing (typically around 10⁻¹⁰ m).
1 mark: Links the observation of the ring pattern to confirmation of wave-particle duality, providing direct evidence of the wave-like behaviour of matter.

