OCR Specification focus:
‘Specific heat capacity relates energy change to mass and temperature change using ΔE = mcΔT.’
Specific heat capacity links the microscopic energy of particles to observable temperature changes, enabling prediction and measurement of how much energy materials absorb or release when heated or cooled.
Understanding Specific Heat Capacity
When a substance is heated, energy is transferred to its particles, increasing their kinetic energy and often their potential energy. This energy transfer raises the temperature, which is a measure of the average kinetic energy of the particles. Different substances require different amounts of energy to achieve the same temperature change, depending on their molecular structure and bonding. This characteristic is quantified by a property known as specific heat capacity.
Specific Heat Capacity: The energy required per kilogram of a substance to raise its temperature by one kelvin (or one degree Celsius) without a change of state.
Specific heat capacity provides a direct link between the microscopic particle motion within a material and its macroscopic thermal behaviour. Substances with strong intermolecular forces, such as water, tend to have high specific heat capacities, while metals, where energy is more easily transferred through delocalised electrons, generally have lower values.
The Energy–Temperature Relationship
The amount of thermal energy transferred, the mass of the material, and its temperature change are quantitatively related by a fundamental equation of thermal physics.
EQUATION
—-----------------------------------------------------------------
Energy Change (ΔE) = mcΔT
ΔE = Energy transferred (joules, J)
m = Mass of the substance (kilograms, kg)
c = Specific heat capacity (joules per kilogram per kelvin, J kg⁻¹ K⁻¹)
ΔT = Change in temperature (kelvin or degrees Celsius, K or °C)
—-----------------------------------------------------------------
This relationship allows one to calculate how much energy is needed to heat or cool a substance by a known amount. The equation applies only when no phase change occurs — the energy simply increases or decreases the internal energy associated with molecular motion rather than breaking or forming bonds.
Between the energy transferred and the resulting temperature change, specific heat capacity acts as a proportionality constant. For a fixed mass, a larger value of c means that more energy is needed for each degree of temperature increase.
Physical Interpretation
Specific heat capacity reflects the internal structure and bonding of a substance. When energy is added:
Kinetic energy of particles increases, leading to faster vibration or motion.
In some materials, part of the energy also increases potential energy by stretching intermolecular bonds.
The extent to which these processes occur determines the magnitude of c.
Substances with many degrees of freedom for energy storage, such as molecular gases or liquids with hydrogen bonding, exhibit large values of c. In contrast, solids with rigid crystal lattices often have smaller capacities because most of the energy goes directly into particle vibration rather than into additional molecular motion.
Internal Energy and Temperature Change
The concept of internal energy—the sum of the random kinetic and potential energies of all particles—lies at the heart of understanding specific heat capacity. When a body is heated and its temperature rises, the increase in internal energy is equal to the energy supplied by heating, assuming no work is done by expansion or contraction.
Thus,
ΔE = ΔU = mcΔT,
where ΔU represents the change in internal energy. The direct proportionality between ΔU and ΔT illustrates how thermal energy affects particle motion and consequently the temperature of the material.
Dependence on Material and Conditions
Specific heat capacity depends on several physical factors:
Nature of the material: Metals typically have low c (around 400 J kg⁻¹ K⁻¹ for copper), while water is exceptionally high (about 4200 J kg⁻¹ K⁻¹).
Temperature range: For many solids, c increases slightly with temperature because higher energy levels become accessible to vibration.
Phase of matter: Solids, liquids, and gases of the same substance exhibit different values of c due to variations in molecular motion and bonding.
Pressure and physical constraints: In gases, specific heat at constant pressure (cₚ) and at constant volume (cᵥ) differ because at constant pressure, energy must also perform expansion work.
Measuring Specific Heat Capacity
Although measurement methods are covered in later subtopics, it is useful to understand the conceptual foundation:
An electrical heater can supply a known energy input, determined from current, voltage, and time.
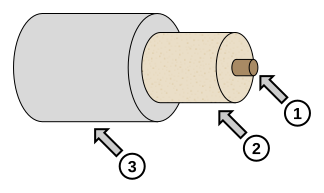
Labeled diagram of a tubular electric heater showing the resistance element (1), electrical insulator (2), and metal casing (3). Such elements convert electrical energy to thermal energy at a known rate, enabling controlled heating in ΔE = mcΔT experiments. The schematic focuses on construction, not on calorimeter surroundings, which are addressed separately. Source.
The temperature rise of a known mass is recorded using a thermometer or temperature sensor.

Simple schematic of a calorimeter showing an insulated vessel with a thermometer and space for the sample and heater. The arrangement minimises heat exchange with the surroundings so the measured ΔT accurately reflects the change in internal energy, supporting use of ΔE = mcΔT. The diagram is intentionally minimal and does not include advanced calorimetry features beyond the syllabus scope. Source.
Using ΔE = mcΔT, the specific heat capacity is calculated once heat losses are corrected for.
The accuracy of experimental results depends on minimising energy losses to the environment and ensuring uniform temperature distribution within the sample.
Practical Importance
Understanding specific heat capacity is essential in both theoretical and applied physics. It governs processes such as:
Thermal management: Designing heating and cooling systems, from radiators to spacecraft shielding.
Climate science: The high specific heat capacity of water stabilises Earth’s temperature, moderating seasonal and daily temperature variations.
Engineering materials: Metals with low c are chosen where rapid temperature change is desirable, whereas materials with high c act as thermal buffers.
Theoretical Insights from Kinetic Theory
From a microscopic perspective, kinetic theory connects the mean kinetic energy of particles with temperature. A rise in temperature signifies that, on average, particles possess greater kinetic energy. The amount of energy required for a given temperature rise depends on:
The number of particles per unit mass, governed by molar mass.
The types of motion accessible to those particles—translational, rotational, and vibrational.
These microscopic details explain why gases and solids with complex molecular structures exhibit distinct specific heat capacities even at the same temperature.
Energy Conservation Context
The principle of energy conservation ensures that any energy transferred to a body either changes its internal energy or does external work. For situations in which there is no phase change and negligible expansion, all the energy supplied as heat changes the internal energy, and thus the temperature. This underpinning principle validates the use of ΔE = mcΔT for calculating temperature changes due solely to heating or cooling within a single phase.
FAQ
Specific heat capacity is the energy required to raise the temperature of 1 kg of a substance by 1 K. Heat capacity, on the other hand, refers to the total energy needed to raise the temperature of an entire object by 1 K, regardless of its mass.
They are related by the equation:
Heat capacity = mass × specific heat capacity (C = mc).
Specific heat capacity is an intrinsic property of a material, while heat capacity is extrinsic, depending on the amount of material present.
Water’s high specific heat capacity (about 4200 J kg⁻¹ K⁻¹) arises from its hydrogen bonding. When energy is added, much of it is used to stretch and break these intermolecular bonds rather than increase kinetic energy immediately.
This means temperature rises slowly because a significant portion of the supplied energy changes potential energy instead of directly increasing particle motion.
As a result, water acts as an excellent thermal buffer, stabilising environmental and biological temperatures.
Different heating methods introduce different experimental uncertainties.
Electrical heating provides a measurable energy input, but losses occur through heat transfer to surroundings.
Immersion in a hot fluid (like water) allows better uniform heating but complicates energy measurement.
Laser or radiant heating may cause surface heating only, leading to inaccurate temperature readings.
Accurate results require uniform heat distribution, minimal losses, and precise control of energy input.
Yes. For most materials, specific heat capacity increases slightly with temperature, especially in solids as atomic vibrations become more energetic and nonlinear.
At very low temperatures, specific heat capacity tends towards zero because atomic motion is restricted.
In liquids and gases, c often varies more significantly because additional energy modes, like rotational and vibrational motion, become accessible at higher temperatures.
For most A-Level experiments, however, c is assumed constant over small temperature ranges.
Not all the energy supplied to a sample stays within it—some is lost to the surroundings via conduction, convection, or radiation.
If these losses are ignored:
The measured temperature rise will be smaller than the true value.
The calculated c will therefore be too high, as the experiment assumes all supplied energy caused the temperature increase.
To correct for losses, insulation, control experiments, or extrapolation techniques (e.g., plotting temperature vs. time) are used to estimate the energy actually absorbed.
Practice Questions
Question 1 (2 marks)
A 0.50 kg block of aluminium is heated and its temperature rises by 15 °C. The specific heat capacity of aluminium is 900 J kg⁻¹ K⁻¹.
Calculate the energy transferred to the block.
Mark scheme:
Correct use of equation ΔE = mcΔT (1 mark)
Substitution and correct calculation: 0.50 × 900 × 15 = 6750 J (1 mark)
Total: 2 marks
Question 2 (5 marks)
A student uses an electrical heater to determine the specific heat capacity of a metal block.
The heater supplies a power of 50 W for 400 s, and the 1.5 kg block’s temperature rises from 20 °C to 35 °C.
The student notices that the block’s surface is warm even before heating stops.
(a) Calculate the specific heat capacity of the block.
(b) Suggest two reasons why the calculated value might differ from the accepted value and explain how these affect the result.
Mark scheme:
(a) Calculation (3 marks)
Correct equation: ΔE = mcΔT (1 mark)
Substitution: 50 × 400 = 1.5 × c × (35 – 20) (1 mark)
Rearrangement and correct answer: c = (20000) / (1.5 × 15) = 888.9 J kg⁻¹ K⁻¹ ≈ 890 J kg⁻¹ K⁻¹ (1 mark)
(b) Discussion (2 marks)
Identifies reasonable experimental limitations (1 mark each, up to 2 marks total), e.g.:
• Energy lost to the surroundings, causing temperature rise to be smaller → calculated c too high.
• Temperature not measured uniformly throughout the block → incorrect ΔT reading.
• Incomplete thermal insulation or poor thermal contact between heater and block → part of the energy not transferred to the block.

