OCR Specification focus:
‘Define moles and use the Avogadro constant NA = 6.02 × 10^23 mol⁻¹ to count particles.’
In thermal and gas physics, understanding the amount of substance and the Avogadro constant provides the essential link between microscopic particles and measurable macroscopic quantities. These ideas enable scientists to count atoms and molecules by measuring mass, connecting the atomic scale to the real world.
The Concept of Amount of Substance
The amount of substance is a fundamental physical quantity in physics and chemistry used to express how many microscopic entities—such as atoms, molecules, or ions—are present in a sample. It allows for direct relationships between macroscopic measurements (mass, volume, pressure) and microscopic particle behaviour.
Amount of substance: The measure of the number of specified particles in a sample, expressed in moles (mol).
The mole provides a bridge between atomic-scale quantities and laboratory-scale measurements. One mole of any substance contains the same number of elementary entities as there are atoms in 12 grams of carbon-12.
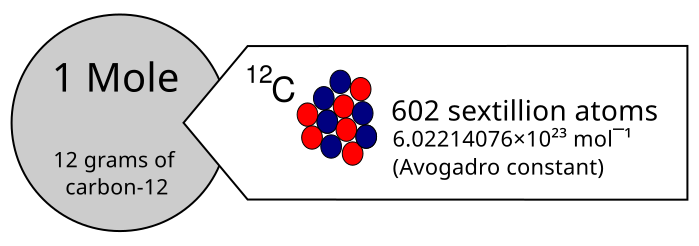
Diagram illustrating one mole using the former carbon-12 definition, linking macroscopic mass (12 g of carbon-12) to a fixed number of entities. This visual anchors the idea that a mole is a count, not a mass. The historical carbon-12 framing is shown; modern SI defines the mole exactly via the Avogadro constant. Source.
This number is known as the Avogadro constant.
The Avogadro Constant
The Avogadro constant, symbolised as NA, defines the number of constituent particles in one mole of a substance. It connects the microscopic world of atoms and molecules to the macroscopic measurements used in experiments.
Avogadro constant (NA): The number of particles per mole of a substance, equal to 6.02 × 10²³ mol⁻¹.
This constant means that one mole of any element or compound contains 6.02 × 10²³ particles, whether they are atoms, molecules, or ions.
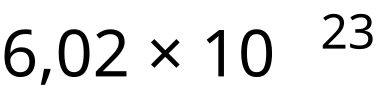
The Avogadro constant displayed in scientific notation as a compact reference. This reinforces that NAN_\text{A}NA has units of mol⁻¹ and represents the number of particles per mole. Source.
For example:
One mole of hydrogen gas (H₂) contains 6.02 × 10²³ molecules of H₂.
One mole of sodium (Na) contains 6.02 × 10²³ atoms of sodium.
The value of NA is derived experimentally from measurements such as the charge on an electron and the Faraday constant in electrolysis.
Relationship Between Particles, Moles, and Mass
The amount of substance, mass, and number of particles are related through the molar mass of the substance. This relationship allows scientists to determine how many atoms or molecules are present in a measurable quantity of material.
EQUATION
—-----------------------------------------------------------------
Number of particles (N) = n × NA
N = number of particles (atoms, molecules, ions) — no unit
n = amount of substance — mole (mol)
NA = Avogadro constant — 6.02 × 10²³ mol⁻¹
—-----------------------------------------------------------------
This relationship shows that multiplying the number of moles by the Avogadro constant gives the total number of constituent particles. Between any two substances, equal amounts in moles contain equal numbers of particles, even if their masses differ drastically.
For example, 1 mol of helium atoms and 1 mol of oxygen molecules both contain 6.02 × 10²³ particles, though their masses differ because of different atomic and molecular masses.
The Mole and Molar Mass
The molar mass is the mass of one mole of a substance, numerically equal to its relative atomic mass (Ar) or relative molecular mass (Mr) expressed in grams per mole (g mol⁻¹). It provides the essential link between mass measurements and the number of particles.
Molar mass (M): The mass of one mole of a substance, expressed in grams per mole (g mol⁻¹).
EQUATION
—-----------------------------------------------------------------
Mass (m) = n × M
m = mass of the substance — kilograms (kg) or grams (g)
n = amount of substance — mole (mol)
M = molar mass — kilograms per mole (kg mol⁻¹) or grams per mole (g mol⁻¹)
—-----------------------------------------------------------------
From this, combining with the earlier equation gives a chain relationship between mass and particles:
N = (m / M) × NA
This links microscopic counts directly to macroscopic quantities, forming the foundation for understanding gases, reactions, and energy changes in thermal physics.
Importance in Ideal Gas Physics
In the ideal gas equation, pV = nRT, the amount of substance n represents the number of moles of gas particles in the system.
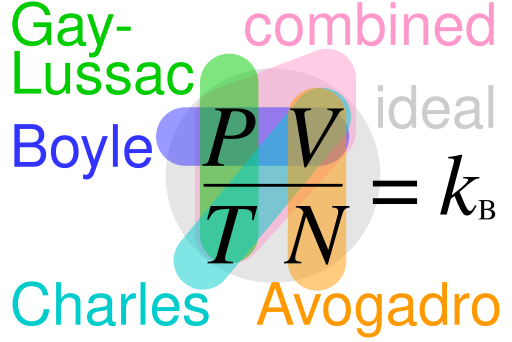
Schematic of Boyle’s, Charles’s, Gay-Lussac’s, Avogadro’s, the combined, and the ideal gas laws, indicating how they interrelate. It situates Avogadro’s law (V ∝ n at constant T,p) alongside the ideal-gas equation that employs n. This diagram includes additional gas-law context beyond the subsubtopic but remains concise and directly supportive. Source.
Without the mole concept, it would be impossible to connect measurable properties like pressure (p), volume (V), and temperature (T) to the microscopic structure of gases.
The Avogadro constant underpins the microscopic interpretation of gas behaviour because it defines how many molecules contribute to pressure through collisions. Each molecule exerts a tiny force, but collectively, 6.02 × 10²³ per mole create measurable macroscopic pressure.
At the molecular level, the average energy and speed of the particles depend on temperature, while the number of particles (linked through NA) determines total internal energy and overall pressure. Hence, n and NA together allow physicists to relate atomic-level motion to observable thermodynamic quantities.
Counting Particles and Comparing Substances
The mole and Avogadro constant allow for meaningful comparison between vastly different substances by equalising particle numbers. Important implications include:
Equal moles of gases at the same temperature and pressure occupy equal volumes. This is known as Avogadro’s law.
Stoichiometric ratios in reactions are expressed in moles, enabling quantitative prediction of reactants and products.
Microscopic properties, such as atomic spacing and density, can be linked to macroscopic measurements via molar mass and NA.
These principles extend across all branches of physics and chemistry, allowing consistent analysis of materials, from solids and liquids to ideal gases.
Determination of the Avogadro Constant
Historically, several experimental methods have determined NA:
Electrolysis measurements, using Faraday’s constant and the known charge of a single electron.
X-ray crystallography, which measures atomic spacing in crystals combined with molar mass and density.
Brownian motion and kinetic theory, where molecular movement is related to observable macroscopic quantities.
These methods converge on the currently accepted value of 6.022 × 10²³ mol⁻¹, reflecting remarkable consistency between theory and experiment.
Summary of Key Relationships
To relate macroscopic quantities to microscopic entities:
Amount of substance (mol) ↔ Number of particles (using NA)
Amount of substance ↔ Mass (using M)
Combined: N = (m / M) × NA
Through these relationships, the Avogadro constant forms the crucial bridge between the atomic scale and laboratory-scale measurements, grounding the study of gases, energy, and thermal physics in precise quantitative science.
FAQ
The Avogadro constant (NA) is a physical constant with units of mol⁻¹, representing the number of particles in one mole of substance.
The term Avogadro number was historically used for the same value but without units. Modern convention specifies the constant form, as it defines a measurable ratio — the number of entities per mole.
Carbon-12 was chosen because it provides a stable, isotopically pure reference that avoids ambiguity between elements with multiple isotopes.
It ensures uniformity across physics and chemistry.
Carbon-12’s atomic structure is well characterised, making precise experimental determination possible.
Using 12 g of carbon-12 as the reference sets the molar mass scale so that relative atomic masses align directly with the molar mass in g mol⁻¹.
Modern methods use X-ray crystallography and silicon sphere experiments.
In the silicon lattice method, scientists measure atomic spacing in a highly pure silicon-28 crystal.
By determining the crystal’s volume and mass, they calculate the number of atoms within.
The ratio of atoms to moles gives NA.
This technique provides extremely precise results and underpinned the 2019 SI redefinition of the mole.
No, it applies to any specified entities — atoms, molecules, ions, electrons, or even formula units.
The key is consistency:
Define what constitutes a single entity before applying NA.
For ionic compounds, NA can refer to formula units rather than individual ions.
For example, one mole of sodium chloride contains 6.02 × 10²³ formula units, each comprising one Na⁺ and one Cl⁻ ion.
The mole links microscopic entities to measurable macroscopic quantities, allowing equations to use practical laboratory values.
It simplifies calculations by:
Replacing enormous particle counts with manageable mole quantities.
Enabling direct proportionality between moles and measurable quantities such as mass or gas volume.
Providing a universal bridge across physics and chemistry for comparing substances on a particle basis.
This unification makes theoretical and experimental data easily comparable.
Practice Questions
Question 1 (2 marks)
Define the term mole and state the value of the Avogadro constant.
Mark scheme:
1 mark for a correct definition:
→ One mole is the amount of substance containing as many elementary entities as there are atoms in 12 g of carbon-12.1 mark for correct value of Avogadro constant:
→ NA = 6.02 × 10²³ mol⁻¹ (accept 6.022 × 10²³ mol⁻¹).
Question 2 (5 marks)
A sample of oxygen gas has a mass of 32.0 g.
(a) Calculate the number of moles of oxygen molecules in the sample.
(b) Determine the number of oxygen molecules in the sample.
(c) Explain why the total number of oxygen atoms in the sample is twice the number of oxygen molecules.
Data:
Molar mass of oxygen, O₂ = 32.0 g mol⁻¹
Avogadro constant, NA = 6.02 × 10²³ mol⁻¹
Mark scheme:
(a) Calculation of moles (2 marks)
Use n = m / M → n = 32.0 / 32.0 = 1.0 mol (1 mark)
Correctly state the number of moles of oxygen molecules = 1.0 mol (1 mark)
(b) Calculation of number of molecules (2 marks)
Use N = n × NA (1 mark)
Substitute correctly: N = 1.0 × 6.02 × 10²³ = 6.02 × 10²³ molecules (1 mark)
(c) Explanation (1 mark)
Each oxygen molecule (O₂) contains two oxygen atoms; therefore, the number of atoms = 2 × number of molecules (1 mark).

