OCR Specification focus:
‘Ideal gas model assumes many particles, negligible volume, elastic collisions, and negligible intermolecular forces.’
The kinetic theory of gases provides a microscopic explanation for the behaviour of gases by modelling them as countless moving particles obeying simple physical laws. This theory underpins the ideal gas model, which connects molecular motion to macroscopic quantities such as pressure, temperature, and volume. By simplifying the complex nature of real gases, the kinetic theory allows physicists to predict and understand thermal and mechanical behaviour accurately under most normal conditions.
The Basis of the Kinetic Theory
The Particle Model of Gases
The kinetic theory describes a gas as a large number of small particles—atoms or molecules—in constant random motion. Each particle moves independently unless it collides with another particle or with the walls of its container. The macroscopic properties of gases, such as pressure and temperature, arise from this microscopic motion and the forces involved in collisions.
The theory’s power lies in its simplifying assumptions, which allow mathematical relationships like the ideal gas equation (pV = nRT) to be derived. These assumptions describe how an ideal gas behaves—one that perfectly follows these simplifications.
The Fundamental Assumptions of the Ideal Gas Model
1. A Very Large Number of Particles
An ideal gas contains an enormous number of particles—typically around 102310^{23}1023 in even small samples.
The number of particles is large enough that statistical averages (such as mean speed or mean kinetic energy) can describe the system accurately.
This allows physicists to apply the laws of probability and derive macroscopic laws from microscopic behaviour.
Random motion ensures no preferred direction, producing uniform properties throughout the gas.
This assumption ensures that the system’s average behaviour remains stable and measurable despite the random nature of individual molecular motion.
2. Negligible Particle Volume
Each gas molecule is assumed to be extremely small compared with the total volume occupied by the gas.
The actual volume of the molecules themselves is considered negligible.
Therefore, the total volume (V) in gas equations represents the volume available for molecular motion, not the physical volume of the particles.
This means that the particles are treated as point masses, having mass but no size.
This simplification becomes less accurate when gases are compressed to high pressures, as the molecular volumes then occupy a more significant fraction of the container.
3. Negligible Intermolecular Forces
It is assumed that there are no attractive or repulsive forces between the particles except during collisions.
Molecules do not interact with each other at a distance.
Between collisions, they travel in straight lines at constant velocity.
The energy of a gas is entirely kinetic, with no contribution from potential energy due to intermolecular forces.
Intermolecular Forces: The attractive or repulsive forces acting between molecules due to charge distributions or induced dipoles.
This assumption allows the internal energy of an ideal gas to depend only on temperature, not on volume or pressure
4. Perfectly Elastic Collisions
All collisions—whether between molecules or between molecules and the container walls—are assumed to be perfectly elastic.
No kinetic energy is lost in collisions; energy is transferred between particles but conserved overall.
Momentum is conserved in every collision, in line with Newton’s laws of motion.
The pressure exerted by the gas arises from these repeated elastic collisions with the container walls.

Idealised elastic collision of two equal-mass particles: the incident particle stops and the target moves off with the incident velocity. This captures energy and momentum conservation in an elastic event, mirroring the molecular-level assumption used in kinetic theory. (Extra contextual detail such as angles is not included here, keeping focus on the core assumption.) Source.
Elastic Collision: A collision in which total kinetic energy and momentum are conserved.
The frequent impacts of molecules on the walls result in an average force per unit area, which defines the pressure (p) of the gas.
Diagram illustrating pressure produced by molecular collisions with a container wall. Each impact changes momentum and imparts a force over an area, defining pressure ppp. The layout is minimal and focuses only on the collision–pressure link required by the kinetic model. Source.
5. Random Motion
Gas molecules move in random directions with a distribution of speeds.
The randomness of motion ensures that the net force and net momentum of all molecules in any direction are zero over time.
This isotropy (uniformity in all directions) is key to deriving scalar quantities such as pressure and temperature.
The molecular speeds are described statistically by the Maxwell–Boltzmann distribution, which gives the proportion of molecules moving at each speed.
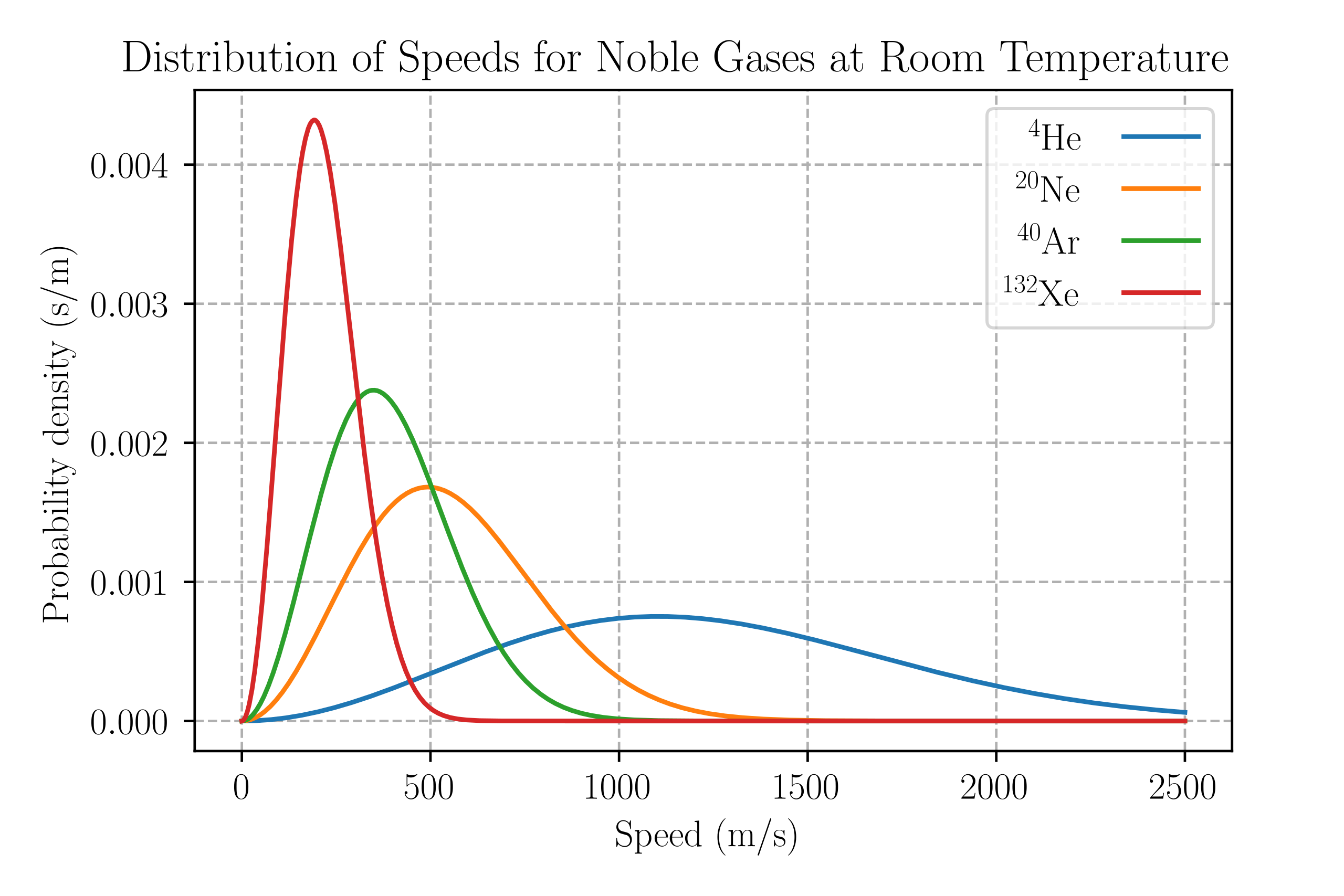
A labelled Maxwell–Boltzmann distribution showing how the fraction of molecules varies with speed. As temperature rises, the peak lowers and shifts to higher speeds, reflecting increased average kinetic energy. This visual directly supports the kinetic-theory linkage between temperature and molecular motion. Source.
EQUATION
—-----------------------------------------------------------------
Mean Kinetic Energy (Ek) = (3/2)kT
k = Boltzmann constant (1.38 × 10⁻²³ J K⁻¹)
T = Absolute temperature in kelvin (K)
—-----------------------------------------------------------------
This relationship shows that temperature is a direct measure of the average kinetic energy of the particles in a gas.
Implications of the Assumptions
Linking Microscopic and Macroscopic Quantities
By combining the above assumptions, physicists can connect the microscopic properties of molecules to macroscopic observables.
Pressure (p) results from molecular collisions transferring momentum to container walls.
Temperature (T) reflects the average kinetic energy of molecules.
Volume (V) provides the space for molecular motion.
These relationships lead to the ideal gas equation, which links these measurable quantities.
EQUATION
—-----------------------------------------------------------------
Ideal Gas Equation (pV = nRT)
p = Pressure (Pa)
V = Volume (m³)
n = Number of moles (mol)
R = Molar gas constant (8.31 J mol⁻¹ K⁻¹)
T = Temperature (K)
—-----------------------------------------------------------------
This equation holds precisely only for an ideal gas, but real gases approximate it closely under low-pressure and high-temperature conditions.
Limitations of the Model
Although the kinetic theory provides a powerful framework, it is an idealisation.
Real gases deviate from ideal behaviour when intermolecular forces or finite molecular volumes become significant.
At high pressures, molecules are forced closer together, increasing the effect of their size and attractive forces.
At low temperatures, reduced kinetic energy allows attractive forces to become more influential, sometimes leading to condensation.
Nevertheless, for most laboratory and atmospheric conditions, the kinetic theory and its assumptions accurately describe gas behaviour, forming a cornerstone of modern thermal physics and statistical mechanics.
FAQ
This assumption simplifies the model by ignoring intermolecular forces, meaning that between collisions, no external forces act on the molecules. Therefore, each particle travels at constant velocity in a straight path until it collides with another molecule or the container wall.
In real gases, weak attractive forces slightly curve these paths, but for most conditions (low pressure and high temperature), the straight-line assumption provides accurate predictions for pressure and temperature relationships.
If collisions were not perfectly elastic, kinetic energy would be lost in each interaction, typically as internal or vibrational energy. Over time, this would reduce the average kinetic energy of the gas molecules.
As a result, the gas temperature would gradually decrease without any energy leaving the system, violating the principle of energy conservation within the kinetic theory framework. Perfect elasticity is therefore essential for maintaining a constant temperature in an isolated ideal gas.
The assumptions themselves remain valid regardless of molecular mass, but molecular mass influences the distribution of molecular speeds.
Lighter molecules have higher average speeds at a given temperature.
Heavier molecules move more slowly on average.
Despite this difference, all gases at the same temperature share the same average kinetic energy, as this depends only on temperature, not on molecular mass.
This supports the universality of the kinetic theory across different gases.
Neglecting intermolecular forces ensures that internal energy depends only on molecular kinetic energy.
If attractive or repulsive forces were significant, some energy would be stored as potential energy, and the pressure would no longer depend solely on the rate of molecular collisions with the container walls.
This assumption is why the ideal gas equation (pV = nRT) works best under conditions where molecules are far apart — typically at low pressure and high temperature.
The assumptions fail when gas molecules are close together or moving slowly enough for intermolecular forces to become important.
At high pressures, molecules occupy a larger fraction of the total volume, violating the negligible-volume assumption.
At low temperatures, reduced kinetic energy allows attractions between molecules to influence behaviour, sometimes leading to condensation.
In such cases, the ideal gas model is replaced by real gas equations, such as the Van der Waals equation, which account for molecular size and forces.
Practice Questions
Question 1 (2 marks)
State two assumptions made in the kinetic theory model of an ideal gas.
Question 1 (2 marks)
Award one mark for each correct assumption (maximum 2 marks).
The gas consists of a very large number of molecules moving in random directions. (1)
The volume of the individual molecules is negligible compared with the total volume of the gas. (1)
No intermolecular forces act except during collisions. (1)
All collisions between molecules and with the container walls are perfectly elastic. (1)
The duration of collisions is negligible compared to the time between them. (1)
Question 2 (5 marks)
Explain how the kinetic theory model accounts for the pressure of a gas in terms of the motion and collisions of its molecules. In your answer, outline the assumptions of the model that are relevant to this explanation.
Question 2 (5 marks)
Award marks as follows:
States that gas pressure arises from molecules colliding with the walls of the container. (1)
Explains that each collision causes a change in momentum of the molecule, resulting in a force on the wall. (1)
Notes that pressure is the total force per unit area due to many collisions. (1)
Links average molecular motion or kinetic energy to temperature — higher temperature increases molecular speed, leading to more frequent or more forceful collisions, increasing pressure. (1)
Correctly references at least two relevant assumptions of the kinetic theory (e.g. elastic collisions, random motion, negligible intermolecular forces). (1)

