OCR Specification focus:
‘Explain gas pressure via Newtonian momentum changes from frequent collisions with container walls.’
In gases, pressure arises from molecular motion. Countless fast-moving particles collide with container walls, transferring momentum and exerting a measurable force per unit area. This microscopic understanding links molecular dynamics to observable gas pressure.
1. Molecular Motion and Collisions
The Kinetic View of Gases
Gases consist of a vast number of tiny, randomly moving particles. Each molecule travels at high speed and changes direction whenever it collides with another particle or a wall. Despite being invisible, these continuous collisions create a steady macroscopic pressure.
Molecules move in random directions with a wide range of speeds.
Elastic collisions occur — total kinetic energy and momentum are conserved.
Between collisions, each particle travels in a straight line at constant velocity.
No significant intermolecular forces act except during collisions.
Newtonian Link to Pressure
According to Newton’s laws of motion, when a molecule collides with the wall, it exerts a force due to its change in momentum. The wall exerts an equal and opposite force back on the molecule, in line with Newton’s third law. The sum of all these molecular impacts generates the gas pressure observed on the macroscopic scale.
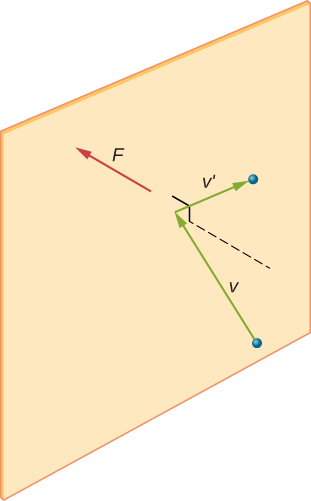
A molecule undergoes an elastic collision with a rigid wall: the momentum component perpendicular to the wall reverses, so the wall experiences an impulse and hence a force. The cumulative effect of many such collisions per second over an area gives the gas pressure. Labels v, v′, and F depict incident velocity, reflected velocity, and wall force respectively. Source.
2. Momentum Change and Force on Container Walls
When a molecule of mass m and velocity component cₓ collides elastically with a wall perpendicular to the x-axis:
The velocity reverses direction from +cₓ to –cₓ.
The change in momentum for the molecule is therefore Δp = –2mcₓ.
By Newton’s third law, the wall experiences an equal and opposite impulse.
The rate at which many such impulses occur gives rise to a steady force, and therefore pressure, on the wall.
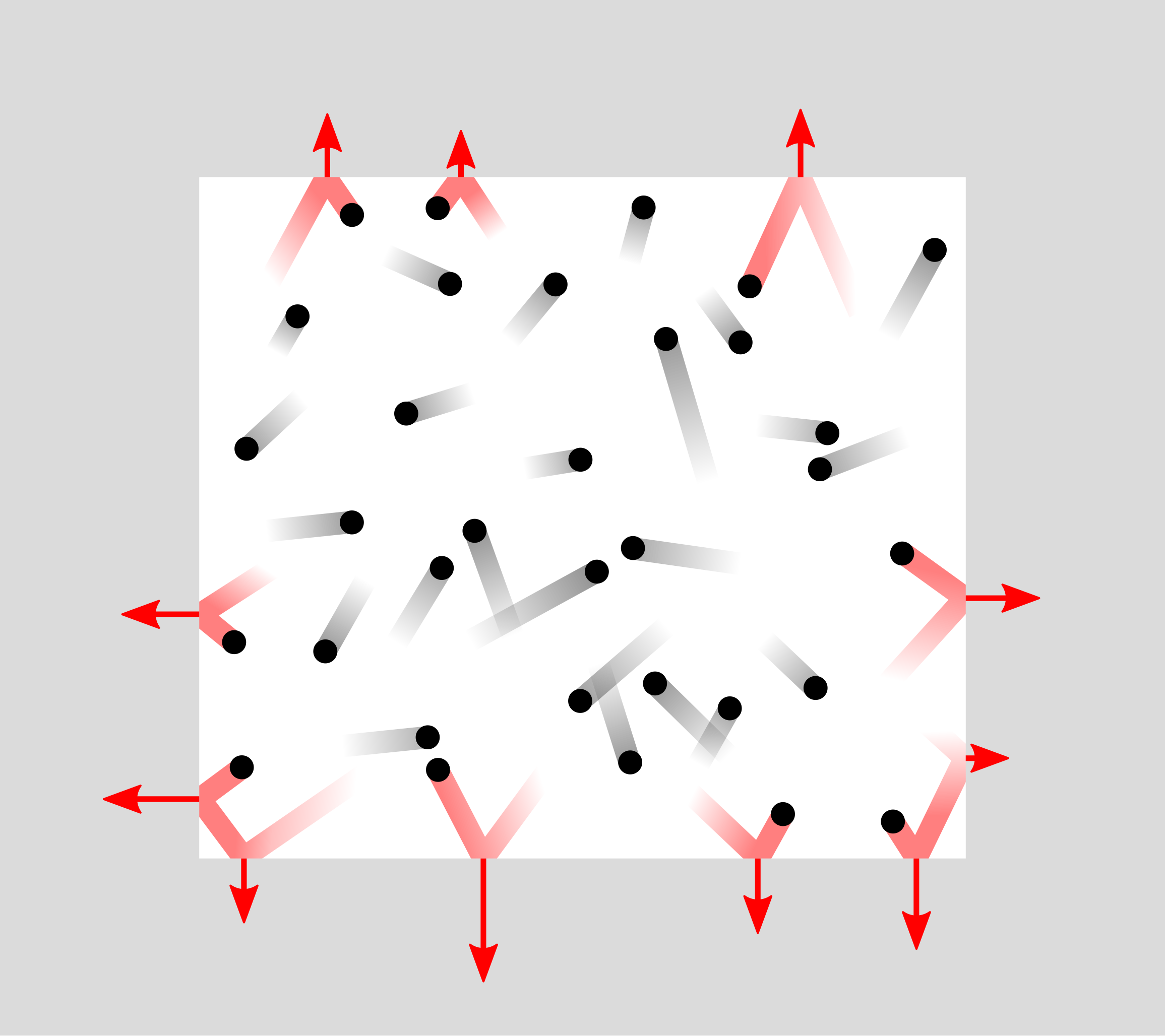
Schematic of gas particles moving randomly and colliding with the walls of a container. Each collision transfers momentum to the wall; the accumulated impulses per second over the wall area constitute the macroscopic pressure. The diagram purposefully abstracts away intermolecular forces to reflect the ideal-gas model used in the notes. Source.
EQUATION
—-----------------------------------------------------------------
Pressure from Molecular Collisions (p) = Force / Area = (Total momentum change per second) / Area
p = (1/3) ρ ⟨c²⟩
p = pressure (Pa)
ρ = density of gas (kg m⁻³)
⟨c²⟩ = mean square speed of molecules (m² s⁻²)
—-----------------------------------------------------------------
This equation relates microscopic particle motion to macroscopic measurable quantities and provides a foundation for the kinetic theory of gases.
3. Statistical Treatment of Many Molecules
Large Number of Particles
In a real gas, the number of molecules (N) is extremely large, typically around 10²³ per mole. It is impractical to track each collision individually, so statistical averages are used.
Mean square speed, ⟨c²⟩, represents the average of the squares of molecular speeds.
Root mean square (r.m.s.) speed, c₍rms₎ = √⟨c²⟩, describes the typical molecular speed.
Molecular speeds follow the Maxwell–Boltzmann distribution, meaning not all molecules move at the same rate.
Directional Averaging
Because molecular motion is random and isotropic (equal in all directions):
The total kinetic energy divides equally among three perpendicular directions (x, y, z).
Therefore, only one third of the total mean square speed contributes to collisions with any single wall, producing the factor of 1/3 in the pressure equation.
This explains why p=(1/3)ρ⟨c2⟩p = (1/3) \rho \langle c^2 \ranglep=(1/3)ρ⟨c2⟩ rather than p=ρ⟨c2⟩p = \rho \langle c^2 \ranglep=ρ⟨c2⟩.
4. Connecting Microscopic and Macroscopic Quantities
Relating Density and Molecular Numbers
If N molecules, each of mass m, occupy a volume V, the gas density is:
EQUATION
—-----------------------------------------------------------------
ρ = (N m) / V
ρ = density of gas (kg m⁻³)
N = number of molecules (no units)
m = mass of one molecule (kg)
V = volume of container (m³)
—-----------------------------------------------------------------
Substituting this into the kinetic pressure relation gives:
EQUATION
—-----------------------------------------------------------------
p V = (1/3) N m ⟨c²⟩
p = pressure (Pa)
V = volume (m³)
N = number of molecules
m = mass of one molecule (kg)
⟨c²⟩ = mean square molecular speed (m² s⁻²)
—-----------------------------------------------------------------
This form connects molecular motion directly to the macroscopic equation of state for an ideal gas.
5. Key Assumptions of the Model
The derivation of pressure from molecular collisions depends on simplifying assumptions known as the kinetic theory assumptions:
Molecules are identical, spherical particles.
The total number of molecules is large enough for statistical averages to be meaningful.
The volume of individual molecules is negligible compared with the container’s volume.
There are no intermolecular forces, except during collisions.
Collisions with walls and between molecules are perfectly elastic.
The time taken for each collision is negligible compared with the time between collisions.
The molecules move randomly and isotropically in all directions.
Each of these ensures the pressure calculated from molecular impacts matches observed gas behaviour under ideal conditions.
6. Physical Interpretation of Pressure
Pressure as Force Distribution
From the molecular perspective, pressure is the result of numerous microscopic forces acting simultaneously on every portion of the container wall. Even though each molecule exerts a minuscule impulse, the cumulative effect of billions of impacts per second yields the measurable macroscopic pressure.
Temperature Connection
The average kinetic energy of gas molecules is proportional to the absolute temperature. Thus, increasing temperature raises ⟨c²⟩, which increases pressure if the volume remains constant. This aligns with Gay-Lussac’s law and provides a molecular explanation for the observed temperature–pressure relationship.
7. Relevance to Real and Ideal Gases
Ideal Gases
An ideal gas strictly follows the kinetic theory assumptions. The expression
pV = (1/3) N m ⟨c²⟩ describes its pressure precisely and leads directly to the familiar ideal gas law, pV = nRT, when statistical and molar relationships are incorporated.
Real Gases
In real gases, deviations occur because:
Intermolecular forces slightly reduce impact momentum.
Molecules have finite volume, affecting the number of collisions.
At high pressures or low temperatures, these effects become significant.
Nevertheless, under moderate conditions, most gases behave closely enough to be treated as ideal, making this molecular collision model a powerful and widely used theoretical framework.
FAQ
The pressure of a gas depends directly on how often and how forcefully molecules collide with the container walls.
If the frequency of collisions increases—either because the molecules are moving faster (higher temperature) or because there are more molecules per unit volume (higher density)—the total rate of momentum transfer rises. This results in a greater average force per unit area, hence higher pressure.
At constant temperature, reducing the volume increases the collision rate proportionally, explaining why pressure rises as volume decreases (Boyle’s law).
Molecular motion is random and occurs equally in all three spatial directions: x, y, and z.
Only one of these directions contributes to collisions with a particular wall at any moment. Because the kinetic energy is equally distributed among the three axes, the average of the square of the velocity in one direction is one third of the total mean square speed.
Hence, only one third of the total molecular kinetic motion contributes to the pressure on any single wall.
Perfectly elastic collisions ensure that no kinetic energy is lost during interactions between molecules or with the container walls.
This assumption keeps the average kinetic energy—and therefore the temperature—constant over time, allowing a steady-state pressure to be defined.
If collisions were inelastic, kinetic energy would be converted into internal or vibrational energy, causing temperature and pressure to decrease with time unless external energy were supplied.
When attractive or repulsive forces act between molecules, collisions are no longer perfectly elastic, and the simple kinetic equation for pressure becomes less accurate.
Attractive forces reduce the effective momentum change on the walls, lowering pressure compared with an ideal gas.
Repulsive forces (dominant at very high densities) can increase pressure beyond ideal predictions.
Such deviations explain why real gases differ from ideal gases, particularly at low temperatures or high pressures.
At a fixed temperature, all gases have molecules with the same average kinetic energy (½m⟨c²⟩).
Lighter molecules have smaller mass but must move faster to maintain that same average energy. Heavier molecules move slower.
Since pressure depends on both molecular speed and number density, the faster movement of lighter particles compensates for their smaller mass, resulting in identical overall pressure when temperature and density are equal.
Practice Questions
Question 1 (2 marks)
Explain, in terms of molecular motion, how a gas exerts pressure on the walls of its container.
Mark Scheme:
(1 mark) Molecules move randomly and collide with the walls of the container.
(1 mark) Each collision changes the molecule’s momentum, exerting a force on the wall; the combined effect of many collisions produces pressure.
Question 2 (5 marks)
A gas consists of N molecules, each of mass m, contained in a cube of side length L. The molecules move randomly in all directions with mean square speed ⟨c²⟩.
(a) Using Newton’s laws, outline how the expression for the pressure of an ideal gas, p = (1/3) ρ⟨c²⟩, can be derived from the motion of the molecules.
(b) State one assumption of the kinetic theory that is necessary for this derivation to hold.
Mark Scheme:
(a)
(1 mark) Considers one molecule colliding elastically with a wall and identifies the change in momentum per collision as 2mcₓ.
(1 mark) States that force on the wall is rate of change of momentum; total force comes from many such collisions per second.
(1 mark) Recognises that only molecules with a velocity component towards that wall contribute, giving an average over all directions.
(1 mark) Uses isotropic motion to state that ⟨cₓ²⟩ = (1/3)⟨c²⟩, leading to p = (1/3)ρ⟨c²⟩.
(b)
(1 mark) Any one valid kinetic theory assumption, e.g. “There are no intermolecular forces except during collisions” or “Collisions are perfectly elastic.”

