OCR Specification focus:
‘Relate macroscopic pressure to mean square speed; define r.m.s. speed and Maxwell–Boltzmann characteristics.’
Microscopic Relation Between Pressure and Molecular Motion
The microscopic relation pV = (1/3)Nm⟨c²⟩ connects the observable properties of an ideal gas to the microscopic behaviour of its molecules. It bridges macroscopic variables such as pressure (p) and volume (V) with molecular-level quantities like mass (m), number of particles (N), and mean square speed (⟨c²⟩). This relationship is central to understanding how gas pressure arises from molecular motion and underpins much of kinetic theory.
Molecular Motion and Pressure in an Ideal Gas
Gas pressure results from the frequent collisions of gas molecules with the container walls. Each molecule exerts a small force upon impact; the sum of all these tiny impulses over time creates a measurable macroscopic pressure. The key idea is that even though the individual molecular motions are random, their collective behaviour obeys predictable statistical patterns.
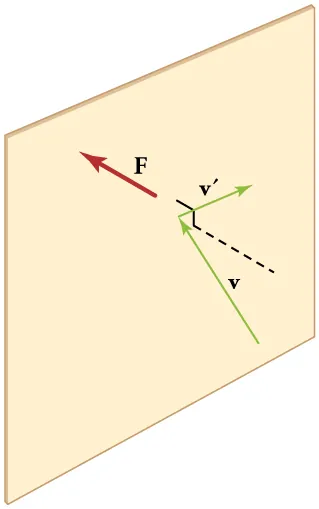
Elastic collisions with a rigid wall reverse the velocity component perpendicular to the wall, so each impact transfers momentum to the wall. The average of many such impulses per unit time and area constitutes pressure. The diagram highlights that only the normal component changes sign; tangential components are unchanged. Source.
The ideal gas model assumes:
A large number of identical particles moving in random directions.
Elastic collisions between particles and container walls (no energy loss).
Negligible molecular volume compared to the total gas volume.
No intermolecular forces, so potential energy between particles is zero except during collisions.
These assumptions allow us to derive the mathematical relationship connecting microscopic motion with pressure.
Derivation Outline of the Relation pV = (1/3)Nm⟨c²⟩
Consider a cubic container with side length L containing N molecules, each of mass m, moving randomly. The derivation begins with analysing the momentum change of a single molecule colliding elastically with a wall and extends to all molecules.
A molecule moving in the x-direction with velocity component cx strikes a wall and rebounds, reversing its velocity in that direction.
The change in momentum per collision is Δp = 2mcx.
The time between successive collisions with the same wall is Δt = 2L / cx.
Therefore, the force exerted by one molecule on the wall is F = Δp / Δt = mcx² / L.
For N molecules moving randomly, the total force is the sum of the contributions from all particles, considering that molecular motion is isotropic (equal in all directions).
Because molecular motion is random and uniform in all directions, on average:
⟨cx²⟩ = ⟨cy²⟩ = ⟨cz²⟩ = (1/3)⟨c²⟩.
Combining these relationships yields the microscopic equation of state:
EQUATION
—-----------------------------------------------------------------
Microscopic Equation of State (pV) = (1/3)Nm⟨c²⟩
p = Pressure (Pa)
V = Volume (m³)
N = Number of molecules
m = Mass of one molecule (kg)
⟨c²⟩ = Mean square speed of the molecules (m² s⁻²)
—-----------------------------------------------------------------
This equation shows that gas pressure arises from the collective momentum transfer of molecular collisions against container walls.
Mean Square Speed and Root Mean Square (r.m.s.) Speed
The mean square speed (⟨c²⟩) represents the average of the squares of all molecular speeds in the gas. Since molecular velocities vary greatly, this statistical average is essential for describing the overall kinetic behaviour.
Mean Square Speed: The average of the squares of molecular speeds in a gas sample.
However, because speed (not velocity) is always positive, we often use the root mean square speed (crms) to express a representative molecular speed.
EQUATION
—-----------------------------------------------------------------
Root Mean Square Speed (crms) = √⟨c²⟩
crms = Typical molecular speed corresponding to average kinetic energy (m s⁻¹)
—-----------------------------------------------------------------
This value allows comparison with temperature and kinetic energy through relationships like ½m⟨c²⟩ = 3/2kT, linking microscopic energy to thermodynamic quantities.
Connecting Microscopic and Macroscopic Descriptions
The equation pV = (1/3)Nm⟨c²⟩ can be compared with the ideal gas law pV = NkT, leading to the relationship between kinetic energy and temperature:
(1/2)m⟨c²⟩ = (3/2)kT.
This shows that the temperature of a gas is directly proportional to the average kinetic energy of its molecules. When temperature increases, molecular speeds rise, and thus the pressure also increases if volume remains constant.
This microscopic interpretation explains the macroscopic behaviour of gases observed through experiments on pressure, temperature, and volume changes.
The Maxwell–Boltzmann Distribution
Not all molecules in a gas move at the same speed; rather, their speeds are distributed according to the Maxwell–Boltzmann distribution, a fundamental concept in kinetic theory.
Maxwell–Boltzmann Distribution: The statistical distribution describing the range of molecular speeds in a gas at a given temperature.
Key characteristics of this distribution include:
A most probable speed (cp) where the curve peaks.
A mean speed (cmean) slightly greater than cp.
A r.m.s. speed (crms) greater than both cp and cmean.
As temperature increases, the distribution curve flattens and shifts to higher speeds, indicating more energetic particles.
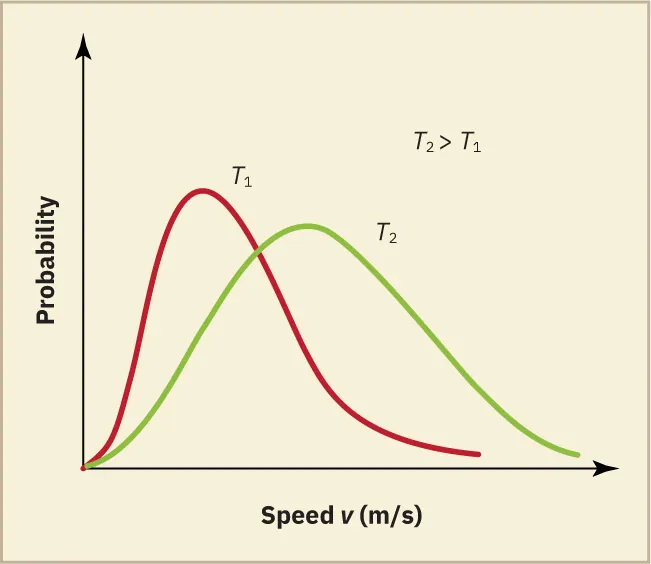
Two Maxwell–Boltzmann curves at different temperatures illustrate that higher T produces a wider distribution with a peak at greater speed. This supports the link between temperature and average molecular kinetic energy. Labels indicate relative peak positions; if any additional markings appear, they simply emphasise the comparison between temperatures. Source.
The area under the curve represents the total number of molecules, which remains constant even as temperature changes.
Physical Interpretation of the Microscopic Equation
Each term in pV = (1/3)Nm⟨c²⟩ has a clear physical meaning:
pV represents the product of pressure and volume — the macroscopic work done by the gas per unit temperature.
(1/3) arises from the equal contribution of motion in three perpendicular directions (x, y, z).
Nm⟨c²⟩ represents twice the total kinetic energy of the gas molecules.
Rearranging gives p = (1/3)(N/V)m⟨c²⟩, showing that pressure is proportional to molecular number density and to the mean kinetic energy of the molecules. This provides a microscopic definition of pressure: the average effect of countless elastic collisions against container walls.
Summary of Core Relationships
To consolidate understanding, note the essential links:
pV = (1/3)Nm⟨c²⟩ — connects pressure, volume, and molecular motion.
pV = NkT — connects macroscopic thermodynamic properties.
½m⟨c²⟩ = 3/2kT — connects kinetic energy and temperature.
Together, these form the foundation of the kinetic theory of gases, enabling interpretation of thermodynamic behaviour through molecular mechanics.
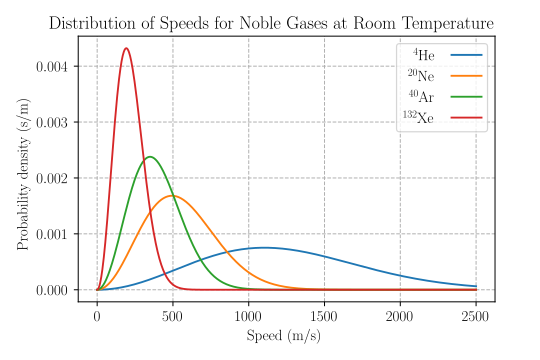
A labeled Maxwell–Boltzmann speed distribution shows how cₚ, c̄, and cᵣₘₛ relate to the curve’s peak and tail. Use it to anchor the terminology of most probable, mean, and r.m.s. speeds. Note: this version also plots different gases at the same temperature to illustrate mass effects (useful context beyond the OCR requirement). Source.
FAQ
The derivation relies on several key assumptions that simplify real gas behaviour to an ideal model:
Molecules are treated as identical, point particles with negligible volume compared to the container.
There are no intermolecular forces except during perfectly elastic collisions.
Collisions are instantaneous and random, conserving kinetic energy and momentum.
The gas has a large number of molecules moving randomly in all directions, producing isotropic pressure.
Violating these assumptions (as in real gases) means the equation becomes an approximation rather than an exact description.
The 1/3 factor arises because molecular motion occurs equally in three perpendicular directions: x, y, and z.
The total mean square speed ⟨c²⟩ can be expressed as:
⟨c²⟩ = ⟨cx²⟩ + ⟨cy²⟩ + ⟨cz²⟩.
Since the gas is isotropic, ⟨cx²⟩ = ⟨cy²⟩ = ⟨cz²⟩ = (1/3)⟨c²⟩.
Only the velocity component perpendicular to a given wall contributes to the momentum transfer producing pressure, so the average effect from all three directions leads to the factor of one third.
At a given temperature, lighter molecules move faster on average than heavier ones. This causes:
The most probable speed and mean speed to be higher for lighter molecules.
The distribution curve for lighter gases to be broader and shifted towards higher speeds.
Heavier molecules to have a narrower distribution centred at lower speeds.
Despite these differences, all gases at the same temperature share the same average kinetic energy (½m⟨c²⟩ = 3/2kT), showing that temperature depends only on energy, not mass.
If molecular speeds increase, ⟨c²⟩ rises, leading to a proportional increase in pressure at constant volume.
When the distribution broadens (e.g. due to heating), more molecules possess higher speeds, resulting in:
Greater momentum change per collision.
More frequent impacts on container walls.
Conversely, cooling narrows the distribution, reducing ⟨c²⟩ and therefore pressure. The macroscopic pressure–volume behaviour (pV = constant at fixed temperature) reflects these microscopic adjustments.
This equation provides the bridge between molecular motion and macroscopic observables.
It links measurable quantities (p, V) with molecular parameters (m, N, ⟨c²⟩).
By combining it with pV = NkT, it establishes that average kinetic energy per molecule is proportional to temperature.
It explains thermodynamic concepts, such as internal energy, in terms of molecular dynamics rather than bulk properties.
Thus, it allows physicists to interpret temperature, pressure, and energy as statistical outcomes of countless microscopic events.
Practice Questions
Question 1 (2 marks)
Explain, using the concept of molecular motion, why the pressure exerted by an ideal gas increases when its temperature rises while the volume remains constant.
Mark scheme:
1 mark for stating that increasing temperature increases the average kinetic energy or speed of the gas molecules.
1 mark for stating that faster-moving molecules collide more frequently or more forcefully with the container walls, increasing the pressure.
Question 2 (5 marks)
(a) State the equation that relates the pressure, volume, and molecular motion of an ideal gas.
(b) Define the term root mean square (r.m.s.) speed.
(c) Use your knowledge of the microscopic model of gases to explain how the equation shows that pressure depends on the mean kinetic energy of the gas molecules.
Mark scheme:
(a) (1 mark)
pV = (1/3)Nm⟨c²⟩ correctly stated.
(b) (1 mark)
Definition: The square root of the average of the squares of molecular speeds in a gas.
(c) (3 marks total)
1 mark for recognising that ⟨c²⟩ is proportional to the mean kinetic energy per molecule, since ½m⟨c²⟩ = 3/2kT.
1 mark for explaining that increasing ⟨c²⟩ (or kinetic energy) leads to higher pressure when the number of molecules and volume remain constant.
1 mark for noting that pressure is caused by molecular collisions with the container walls, and greater kinetic energy produces larger momentum changes per collision, increasing pressure.

