OCR Specification focus:
‘A constant net force perpendicular to velocity causes motion along a circular path.’
Objects moving in circular paths experience a continuous change in direction. Although the speed remains constant, the velocity constantly changes due to its direction, requiring a net force acting perpendicular to velocity. This perpendicular force produces circular motion without altering the object’s speed, only its direction.
Understanding Circular Motion
When an object moves in a circle, even at constant speed, it is accelerating because velocity is a vector quantity, dependent on both magnitude (speed) and direction. The continual change in direction means that the velocity is not constant, so acceleration must be present. This type of acceleration, directed towards the centre of the circle, is known as centripetal acceleration. The force responsible for this acceleration is the centripetal force.
The key idea here is that a net force acting perpendicular to an object’s instantaneous velocity causes the object to follow a circular path rather than a straight line.
Centripetal Force: The net force directed towards the centre of a circular path that keeps an object moving in circular motion.
The Role of the Perpendicular Force
In uniform circular motion, the net force is always perpendicular to the velocity. This perpendicularity ensures that:
The force changes the direction of the velocity vector, not its magnitude.
The speed of the object remains constant.
The path of motion forms a circle, as the direction of velocity continuously changes while maintaining constant speed.
If the force were not perpendicular, a component of the force would act along the direction of motion, altering the object’s speed. Therefore, only when the net force is entirely perpendicular can an object maintain constant speed in a circular path.
Connection Between Force, Velocity, and Acceleration
The relationship between force, velocity, and acceleration in circular motion follows directly from Newton’s Second Law. A net force must produce an acceleration in the same direction as the force. In circular motion:
The acceleration is directed towards the centre of the circle (centripetal).
The velocity is tangential to the circle at any instant.
The force and acceleration are perpendicular to the velocity.
EQUATION
—-----------------------------------------------------------------
Centripetal Acceleration (a) = v² / r
a = Centripetal acceleration (m s⁻²)
v = Linear speed (m s⁻¹)
r = Radius of circular path (m)
—-----------------------------------------------------------------
Although this expression quantifies the acceleration, in this subsubtopic the focus remains conceptual — understanding that this acceleration arises because a perpendicular force continually redirects the velocity vector towards the centre.
Between any two consecutive instants, the object moves along a short arc, and its velocity vector rotates slightly towards the centre. The net force is what causes this continual redirection.
Visualising the Perpendicular Force
To visualise this, imagine an object moving in a circle at constant speed:
The velocity vector is always tangent to the circle.
The net force vector points towards the centre (perpendicular to velocity).
The direction of the force changes continuously as the object moves.
The magnitude of the force remains constant if the speed and radius are constant.
If the force is removed suddenly (for example, if a string breaks while whirling a ball), the object will no longer move in a circle. It will continue moving in a straight line tangent to the circle at that point, in accordance with Newton’s First Law. This shows that without a perpendicular net force, circular motion cannot be sustained.
The Continuous Change of Velocity
Even though speed is constant, the velocity vector rotates as the object moves around the circle. This rotation is caused by the centripetal acceleration. The direction of this acceleration is always towards the centre, while the direction of velocity is tangential.
At any instant:
The velocity and acceleration are perpendicular.
The force (centripetal) has no component along the velocity direction.
The work done by the force on the object is zero, because work requires a force component along the displacement, and here the displacement is always tangential.
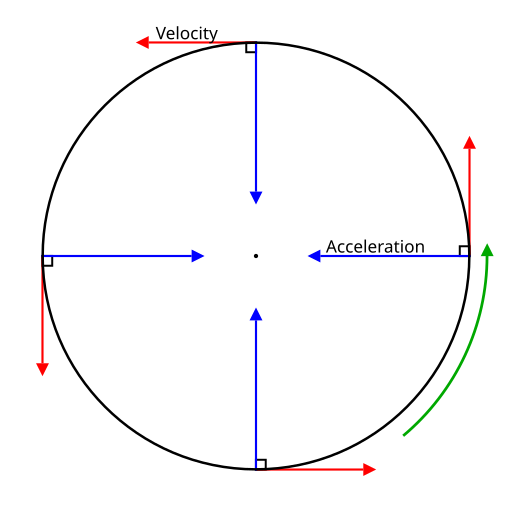
Uniform circular motion with tangential velocity and radial (centripetal) acceleration shown at a point on the path. The inward acceleration reflects a net force perpendicular to velocity, turning the object without changing its speed. The diagram is deliberately minimal to focus on direction, not magnitude. Source.
Work Done: The energy transferred when a force acts through a displacement in the same direction as the force.
Since the force is perpendicular to displacement at every instant, no work is done, meaning the kinetic energy and speed remain constant during uniform circular motion.
Examples of Perpendicular Forces in Action
There are many real-world cases where a perpendicular net force results in circular motion:
Gravitational force acts as the centripetal force keeping planets in orbit around the Sun.
Tension in a string provides the necessary force for a conical pendulum or a whirling bung.
Friction between tyres and the road enables a car to turn along a curved path.
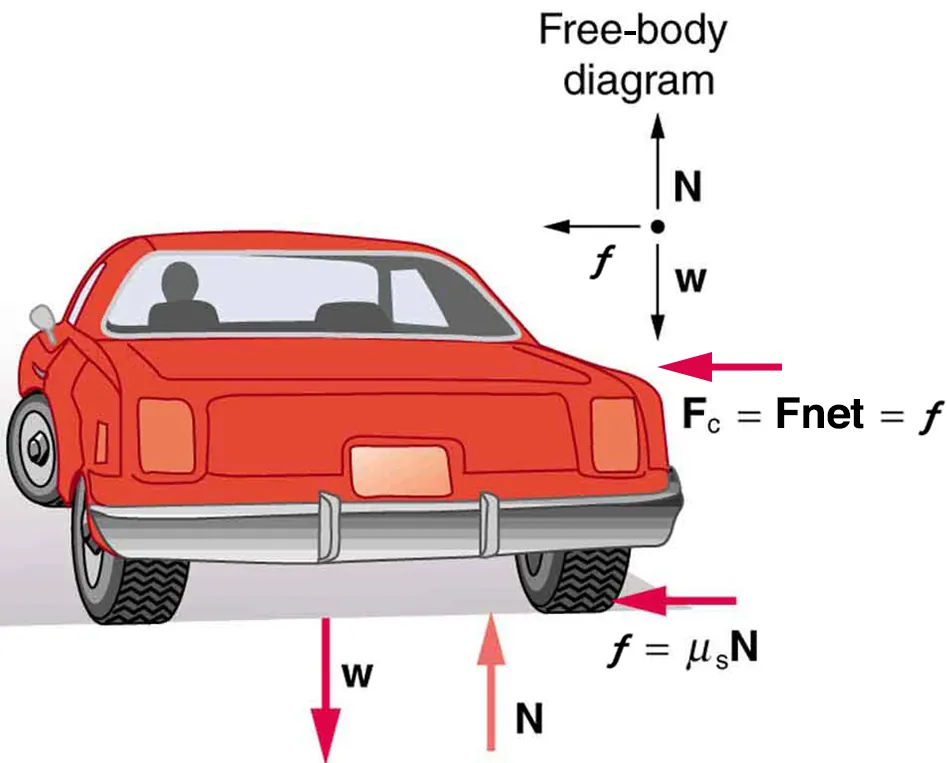
Free-body diagram of a car negotiating a level curve: weight (w) and normal reaction (N) act vertically, while static friction provides the horizontal centripetal force towards the curve’s centre. Because this force is perpendicular to the car’s velocity, it changes direction but not speed. Note: the diagram also names the forces (w, N) for completeness. Source.
Electrostatic or magnetic forces cause charged particles to move in circular paths within fields.
In each of these examples, the key feature is that the net force always acts towards the centre of the circular path, perpendicular to the velocity, maintaining circular motion.
Summary of Key Points within this Specification Focus
A constant net force that is perpendicular to velocity results in circular motion.
The direction of the velocity changes, but its magnitude (speed) remains constant.
The net perpendicular force provides centripetal acceleration directed towards the centre.
No work is done by the centripetal force, as the force and velocity are perpendicular.
Without this perpendicular force, an object would move in a straight line, not a circle.
These relationships define the essential physics of uniform circular motion, as required by the OCR specification.
FAQ
Centripetal force is not a distinct type of force; it is the resultant (net) force acting towards the centre of the circular path.
Depending on the situation, this resultant can come from:
Tension (as in a whirling bung or pendulum)
Gravity (for orbiting planets)
Friction (for vehicles turning on a road)
Electrostatic or magnetic forces (for charged particles in fields)
The key idea is that these forces combine to provide the necessary inward acceleration, rather than being an additional new force acting separately.
Not always. A perfectly constant perpendicular force of fixed magnitude and direction relative to the moving object’s position is required for uniform circular motion.
If the magnitude of the perpendicular force varies, or if it’s not directed precisely towards a fixed centre, the object may move in an elliptical or irregular path instead of a circle.
This distinction is crucial in orbital motion, where gravitational force changes with distance, resulting in elliptical rather than circular orbits.
A smaller radius means a larger required centripetal force to maintain circular motion.
From the relationship F ∝ 1/r when speed is constant, halving the radius doubles the necessary inward force.
In practical terms:
Tightening the radius of a car’s turn demands greater tyre friction.
A shorter string in a whirling bung setup requires higher tension.
If the available inward force cannot increase accordingly, the object will no longer maintain the circular path and may move outward tangentially.
In uniform circular motion, the force only changes the direction of velocity, not its magnitude.
Because the force is always exactly perpendicular to the velocity, there is no component of force along the motion, and therefore no change in speed or radius.
An inward spiral would occur only if:
There were a component of force along the velocity (doing work), or
The magnitude of the inward force increased while the speed remained constant.
A simple classroom demonstration uses a rubber bung on a string swung in a horizontal circle.
The tension in the string acts as the perpendicular (centripetal) force.
As the bung moves faster, the tension increases, keeping it in circular motion.
Releasing the string instantly shows the tangential path, confirming that the force only directed the motion, not maintained the speed.
This setup clearly visualises how a constant perpendicular net force produces circular motion, directly aligning with the concept in this subsubtopic.
Practice Questions
Question 1 (2 marks)
An object moves at constant speed in a horizontal circular path. Explain why a force must act on the object and describe the direction of this force.
Mark Scheme
1 mark: States that a force is required because the object’s velocity is constantly changing direction, meaning it is accelerating.
1 mark: States that the force acts towards the centre of the circle (is perpendicular to the velocity).
Question 2 (5 marks)
A small ball is attached to a string and whirled in a horizontal circle at constant speed.
(a) Explain why the ball is accelerating even though its speed does not change.
(b) State the direction of the acceleration and the net force acting on the ball.
(c) Describe what would happen to the motion of the ball if the string were to break suddenly.
(d) Explain why the force acting on the ball does no work during circular motion.
Mark Scheme
(a) (2 marks)
1 mark: Recognises that velocity changes direction continuously in circular motion.
1 mark: Explains that acceleration is caused by the change in direction of velocity, not by a change in speed.
(b) (1 mark)
1 mark: States that both acceleration and force act towards the centre of the circle (are centripetal).
(c) (1 mark)
1 mark: States that if the string breaks, the ball moves in a straight line tangent to the circle at the point of release (due to Newton’s First Law).
(d) (1 mark)
1 mark: Explains that the force is perpendicular to the velocity/displacement, so no work is done and the kinetic energy remains constant.

