Constant Speed and v = ωr

Circular motion occurs when an object moves along a circular path at a fixed radius from a central point. In uniform circular motion, the object travels at a constant speed, although its velocity—which includes both magnitude and direction—continually changes because its direction is always tangential to the circle. Understanding how speed, angular velocity, and radius are related is crucial to describing this motion mathematically and conceptually.

Understanding Constant Speed in Circular Motion

When an object moves in a circle at constant speed, the magnitude of its velocity does not change. However, since its direction continuously alters as it moves around the circle, the object experiences an acceleration even though its speed remains unchanged. This is known as centripetal acceleration, and it points towards the centre of the circle.

The concept of constant speed in this context differs from constant velocity, because velocity is a vector quantity dependent on both speed and direction. The key idea is that while the magnitude of velocity (speed) remains constant, its direction does not.

Objects moving at constant speed in circular paths can include:

• A satellite orbiting the Earth at a steady orbital speed.

• A car rounding a circular track at a constant speed.

• A point on the rim of a spinning wheel.

These examples demonstrate that even with no change in speed, there is always a net force directed toward the circle’s centre to maintain the motion.

Relationship Between Linear and Angular Quantities

To link linear speed with angular motion, we must recognise that circular motion can be described using both linear and rotational quantities.

When an object moves along a circular path of radius r, it covers a linear distance s related to the angle it sweeps out, measured in radians.

EQUATION
—-----------------------------------------------------------------
Arc Length (s) = rθ
s = Linear distance along the circular path (metres, m)
r = Radius of the circular path (metres, m)
θ = Angle subtended at the centre (radians, rad)
—-----------------------------------------------------------------

As the object moves, the rate at which it sweeps out angle θ defines its angular velocity, symbolised by ω.

For uniform circular motion, ω is constant, because the angle increases at a steady rate.

The Core Relationship v = ωr

The linear (tangential) speed v of an object moving in a circle is directly related to its angular velocity and radius through the following equation:

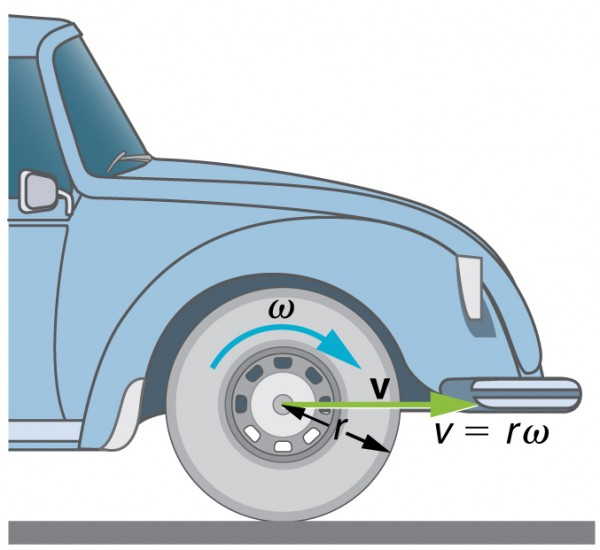
For a rolling wheel, the tread speed vvv equals the car’s forward speed, while the wheel’s angular velocity ω\omegaω and radius rrr satisfy v=rωv=r\omegav=rω. Increasing ω\omegaω or rrr increases the linear speed. The schematic labels vvv and ω\omegaω explicitly for clarity. Source.

EQUATION
—-----------------------------------------------------------------
Linear Speed (v = ωr)
v = Tangential speed (metres per second, m s⁻¹)
ω = Angular velocity (radians per second, rad s⁻¹)
r = Radius of circular path (metres, m)
—-----------------------------------------------------------------

This relationship expresses that the linear speed of a point on a rotating object is proportional to both its angular velocity and its distance from the axis of rotation. Therefore, points further from the centre move faster linearly, even though all points share the same angular velocity.

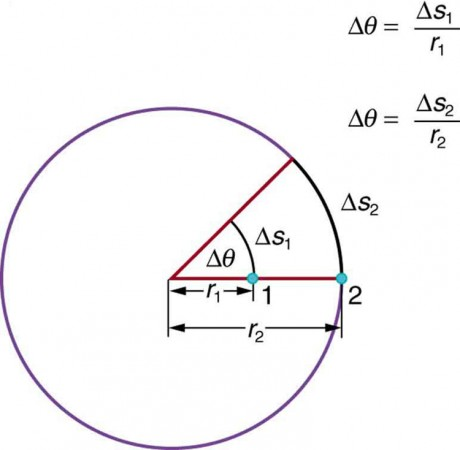
Two points on a rotating disk at different radii traverse different arc lengths in the same time, so their tangential speeds differ while ω\omegaω is common to the whole disk. This visually encodes the proportionality v∝rv\propto rv∝r for uniform ω\omegaω. Source.

For example, the edge of a rotating disc moves faster than a point halfway towards its centre, though both complete one rotation in the same time.

Constant Speed and Directional Change

Although the speed is constant in uniform circular motion, directional change is continuous. The velocity vector at any instant is tangential to the circle.

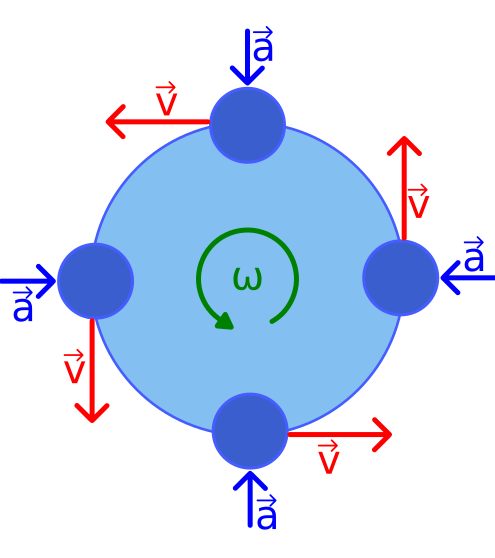
A particle in uniform circular motion has instantaneous velocity vvv tangent to the path, centripetal acceleration aaa toward the centre, and angular velocity ω\omegaω along the rotation axis. The diagram emphasises constant speed with continuously changing direction. Labels match OCR terminology and support the relation v=ωrv=\omega rv=ωr. Source.

As the object moves, this vector rotates with the same angular velocity as the object itself. This means:

• The magnitude of velocity (speed) stays constant.

• The direction of velocity changes constantly.

• There must be a centripetal force acting toward the centre to change the direction.

The constancy of speed results from a balance of forces where no tangential force accelerates or decelerates the object. Only the centripetal force, perpendicular to motion, acts to redirect the velocity.

Interpreting ω and v Physically

Understanding the relationship between angular and linear quantities provides a useful bridge between rotational and linear kinematics:

• ω (angular velocity) tells us how fast the object rotates through an angle.

• v (linear speed) tells us how fast a point on the circle moves along the arc.

In essence, ω gives the rotational description, while v gives the spatial description of the same motion. This duality is essential for connecting rotational equations with linear dynamics.

For instance:

• If ω increases, v increases proportionally, assuming r remains constant.

• If r increases while ω stays constant, the object covers more distance in the same angular interval, so v again increases.

These proportional relationships underpin much of the physics of rotational systems, from simple spinning masses to orbital mechanics.

Application to Uniform Circular Motion

Uniform circular motion implies both constant angular velocity and constant linear speed. This allows the derivation of time-related quantities such as period (T) and frequency (f), though their explicit formulae are part of adjacent subtopics. What remains central here is recognising that for uniform rotation:

• ω is constant.

• r is constant.

• v = ωr ensures linear speed remains constant.

If either ω or r changes, the motion ceases to be uniform. Thus, maintaining constant speed depends on stable rotational conditions.

Conceptual Summary of v = ωr

This relationship encapsulates the connection between how fast an object spins (angular velocity) and how fast it moves along its circular path (linear speed). It illustrates that:

• Linear speed depends on both rotation rate and radius.

• All points share the same angular velocity but have different linear speeds depending on their distance from the centre.

• Constant speed in circular motion implies no tangential acceleration, even though there is always centripetal acceleration.

By mastering this link, students gain a clear understanding of how rotational motion translates into real-world linear motion in systems as varied as turning wheels, orbiting planets, and spinning machinery.