When an object moves in a circular path at constant speed, it experiences continuous change in velocity direction. This change requires acceleration directed towards the circle’s centre.

Understanding Centripetal Acceleration

Circular motion involves an object travelling around a fixed point or axis. Although the speed remains constant during uniform circular motion, the velocity is continually changing because its direction changes constantly. Since acceleration is the rate of change of velocity, this change in direction implies a continuous acceleration — the centripetal acceleration.

The term centripetal comes from Latin, meaning “centre-seeking,” and it refers to the acceleration (and hence force) directed towards the centre of the circular path that maintains the object’s curved trajectory.

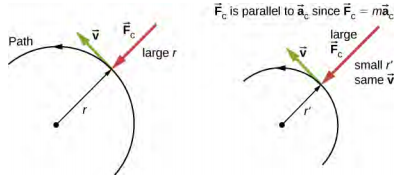
A clean diagram of uniform circular motion showing the tangential velocity (v) and the inward-directed centripetal acceleration (a₍c₎). It illustrates the perpendicular relationship between these two vectors and the centre-seeking nature of the acceleration. Source.

Nature and Direction of Centripetal Acceleration

Centripetal acceleration is always perpendicular to the object’s instantaneous velocity and points towards the centre of rotation. This ensures that the object stays on its circular path instead of moving off in a straight line.

If the force producing this acceleration were suddenly removed, the object would continue in a straight line tangentially to the circle, in accordance with Newton’s First Law of Motion.

Relationship between Linear and Angular Quantities

To describe circular motion precisely, it is important to relate linear and angular quantities.

• Linear speed (v) measures the rate of change of arc length around the circle.

• Angular velocity (ω) measures the rate of change of angle in radians per second.

These two quantities are connected through the radius (r) of the circle.

EQUATION
—-----------------------------------------------------------------
Linear speed and angular velocity (v = ωr)
v = linear speed (metres per second, m s⁻¹)
ω = angular velocity (radians per second, rad s⁻¹)
r = radius of circular path (metres, m)
—-----------------------------------------------------------------

This fundamental relationship provides a bridge between rotational and translational descriptions of motion, allowing different forms of the centripetal acceleration equation to be expressed interchangeably.

Deriving the Expression for Centripetal Acceleration

For an object moving in a circle of radius r at a constant speed v, its direction changes continuously. Using geometrical and vector reasoning, it can be shown that the magnitude of the acceleration is proportional to the square of the speed and inversely proportional to the radius.

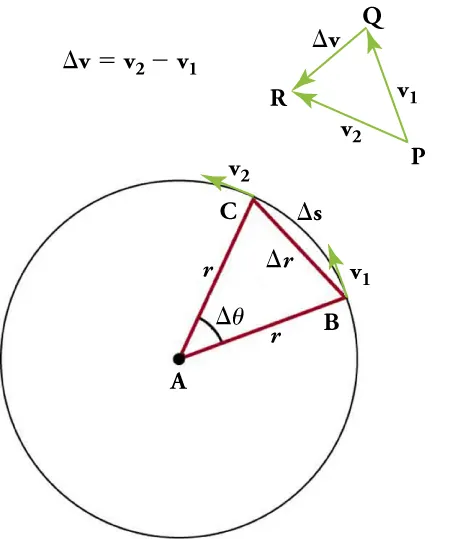
A geometric construction showing velocity vectors at two points on a circular path. The inward-pointing Δv vector closes the triangle, explaining why the resulting acceleration is directed toward the centre. This figure includes extra derivational detail (the Δv triangle) for conceptual clarity. Source.

EQUATION
—-----------------------------------------------------------------
Centripetal Acceleration (a = v²/r)
a = centripetal acceleration (metres per second squared, m s⁻²)
v = linear speed (metres per second, m s⁻¹)
r = radius of circular path (metres, m)
—-----------------------------------------------------------------

Substituting the relationship between linear and angular speed (v = ωr) gives an alternative but equivalent form:

EQUATION
—-----------------------------------------------------------------
Centripetal Acceleration (a = ω²r)
a = centripetal acceleration (metres per second squared, m s⁻²)
ω = angular velocity (radians per second, rad s⁻¹)
r = radius of circular path (metres, m)
—-----------------------------------------------------------------

These expressions are fundamental to analysing circular motion and appear throughout rotational dynamics, orbital mechanics, and mechanical systems such as turbines and wheels.

Key Characteristics of Centripetal Acceleration

Constant Magnitude and Changing Direction

• For uniform circular motion, the magnitude of velocity remains constant but its direction changes.

• Consequently, centripetal acceleration changes direction continuously, always pointing towards the centre.

• The vector of acceleration thus rotates synchronously with the object’s motion, maintaining a constant magnitude.

Dependence on Radius and Speed

• The expression a = v²/r shows that centripetal acceleration increases with the square of the speed and decreases as radius increases.

• Therefore, for a given speed, a smaller radius demands a larger centripetal acceleration, meaning greater inward force is required to maintain the path.

• Conversely, increasing the radius for the same speed lowers the required acceleration.

Physical Interpretation and Examples

Centripetal acceleration represents the continuous inward change in velocity direction necessary to keep an object moving along a circular trajectory. In real-world systems:

• A car turning around a roundabout experiences centripetal acceleration provided by friction between tyres and road.

• A planet orbiting a star experiences centripetal acceleration due to the gravitational force acting towards the star.

• An electron in a magnetic field moves in a circular path because the magnetic force supplies the required inward acceleration.

These examples highlight that the source of centripetal force varies depending on the physical system, but the acceleration behaviour remains the same in all cases.

The Vector Nature of Centripetal Acceleration

The centripetal acceleration vector is always directed radially inward and is perpendicular to the velocity vector, which is tangential to the circle. This perpendicular relationship ensures that acceleration changes the direction of motion but not its speed.

This feature distinguishes centripetal acceleration from tangential acceleration, which changes the magnitude of speed in non-uniform circular motion. In uniform circular motion, tangential acceleration is zero, and the total acceleration is purely centripetal.

Conceptual Summary of Relationships

To clarify the interconnections between quantities involved in circular motion:

• Linear quantities: speed (v), acceleration (a), and displacement (arc length s).

• Angular quantities: angular velocity (ω), angular acceleration (α), and angle (θ).

• The two sets are linked by the radius (r) of the circle, forming the core relationships:

  • v = ωr

  • a = ω²r

  • s = rθ

These relationships form the mathematical framework necessary to describe rotational motion in a linear context, making them central to the analysis of circular dynamics.

Importance in Physics

Understanding centripetal acceleration is essential to grasp how forces produce circular motion without altering speed. It underpins much of mechanics, from vehicle dynamics and orbital motion to rotating machinery. OCR A-Level Physics expects students to use and manipulate both expressions (a = v²/r and a = ω²r) fluently in analysing uniform circular motion systems and understanding the physical meaning of centripetal acceleration — the acceleration directed towards the centre of a circular path that keeps an object moving in that path.