OCR Specification focus:
‘Model a spherically symmetric mass as a point mass located at its centre.’
Spherically symmetric astronomical bodies can be treated as point masses to simplify gravitational analysis, allowing predictable field behaviour and enabling accurate modelling of planetary, stellar, and orbital dynamics.
Modelling Spherical Masses as Points
The idea that a spherically symmetric mass may be represented as a point mass located at its centre is a crucial simplification in gravitational physics. This approach allows the gravitational influence of large, complex objects to be described using the same mathematical form as that for small point-like objects. Understanding how and why this simplification works provides essential grounding for later study of gravitational fields, orbital mechanics, and potential energy.
Conditions for Treating a Sphere as a Point Mass
A spherical mass can only be modelled as a point mass when specific physical conditions are satisfied. These conditions ensure that the gravitational effects outside the object behave as if all the mass were compressed into a single point.
The mass distribution must be spherically symmetric.
This means the object must have the same mass at every point on any spherical shell centred on its core.The object must be considered from a point outside its radius.
The simplification applies only to external points; gravitational behaviour inside a spherical body requires different treatment.The density may vary with radius, but symmetry must be preserved.
Many realistic bodies, such as planets, have layered structures yet still satisfy spherical symmetry.
These conditions, taken together, justify collapsing the object's mass to a point in theoretical models.
Spherical Symmetry and Its Physical Basis
In physics, spherical symmetry refers to a situation in which all directions outward from the centre of an object are equivalent in terms of mass distribution. Once this symmetry is established, the gravitational influence depends only on the distance from the centre, not the direction.
Spherical Symmetry: A mass distribution in which the density depends only on distance from the centre, giving identical properties in every radial direction.
This definition helps students appreciate why gravitational fields from such bodies display predictable radial patterns. The symmetry ensures that contributions from all mass elements combine to replicate the effect of a single mass point.
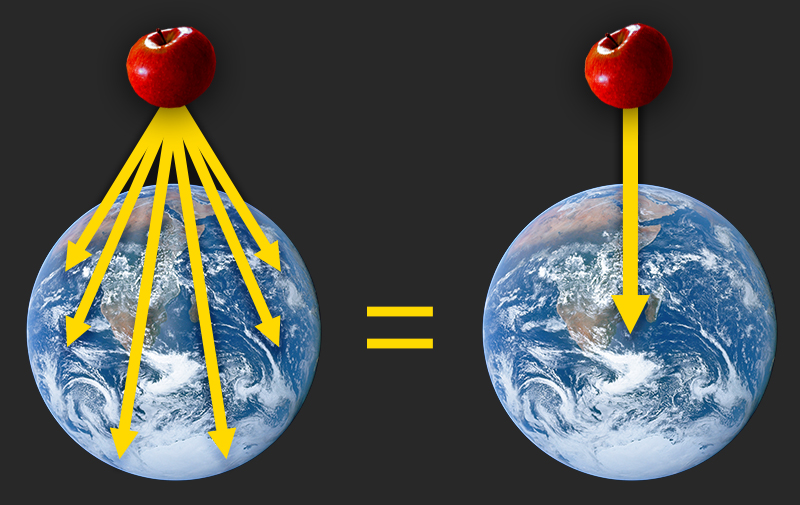
Multiple gravitational pulls from different parts of Earth combine into a single resultant force directed at the planet’s centre, illustrating why a spherical mass behaves like a point mass for external points. Source.
After establishing the symmetry, the gravitational field produced by the sphere becomes easier to describe using standard gravitational relationships. This simplification is foundational to A-Level gravitational calculations involving planets, moons, stars, and artificial satellites.
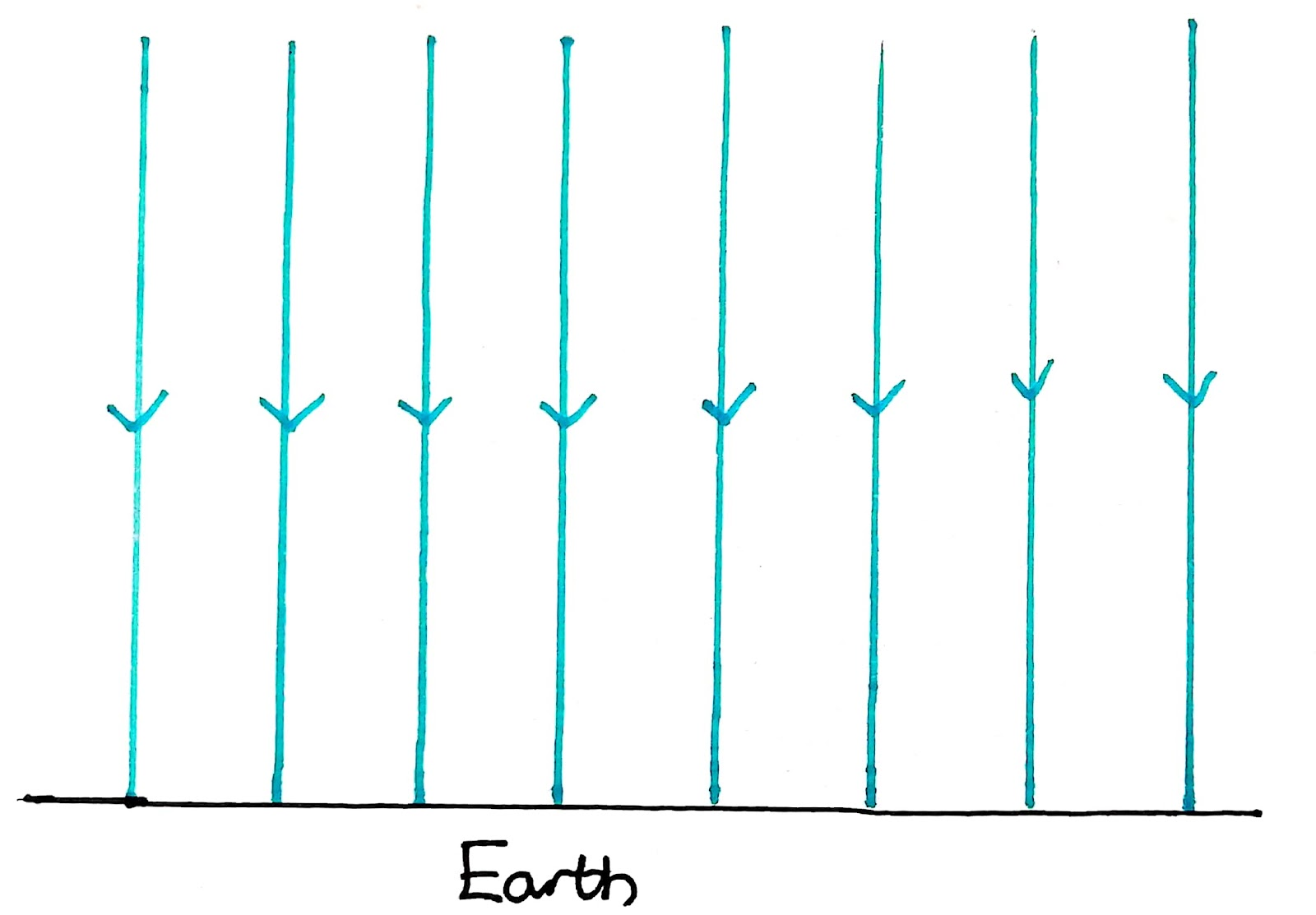
Radial arrows pointing towards Earth indicate that the gravitational field depends only on distance from the centre, while the red equipotentials show related potential surfaces (included here as extra detail). Source.
The Concept of a Point Mass in Gravitational Modelling
A point mass is an idealised object whose entire mass is concentrated at an infinitesimally small point. Although impossible in the real world, this abstraction allows mathematical expressions to describe gravitational forces and fields accurately for symmetric objects.
Point Mass: An idealised object with mass concentrated at a single point in space, used to simplify gravitational and mechanical analysis.
In modelling terms, once a spherical mass is treated as a point mass, its gravitational influence at external points is identical to that predicted by Newton’s law of gravitation. This means that complex interior structure becomes irrelevant for calculating external field strength.
A brief sentence between blocks ensures clarity of connection between conceptual ideas.
Why the Point-Mass Model Works
The justification for modelling a sphere as a point mass comes from mathematical proofs within Newtonian mechanics. The key result can be summarised as follows:
Outside a spherically symmetric distribution, the gravitational field behaves exactly as if all mass were at the centre.
Inside the sphere, the field varies differently, decreasing towards zero at the centre; this behaviour is outside the scope of this subsubtopic.
This behaviour leads to powerful simplifications in gravitational field analysis.
EQUATION
—-----------------------------------------------------------------
Gravitational Field of a Spherical Mass (g) = −GM/r²
G = Gravitational constant (N m² kg⁻²)
M = Mass of the spherical object (kg)
r = Distance from the centre of the mass (m)
—-----------------------------------------------------------------
Although this equation is derived elsewhere in the specification, including it here reinforces how the point-mass model enables such a concise mathematical description. The relationship works only because the mass has been collapsed conceptually to the centre.
A normal explanatory sentence supports students in applying this equation appropriately within this topic.
Applications of the Point-Mass Approximation
Understanding when to treat spheres as point masses is vital in many physical contexts involving gravitational interactions. OCR A-Level Physics learners will routinely use this approach in later topics.
Key situations where the point-mass model is essential include:
Modelling planets and moons for orbital studies.
Their overall shape and internal composition can be ignored for gravitational calculations at large distances.Determining gravitational field strength around stars or large spherical bodies.
External field behaviour fits the inverse-square law precisely due to effective point-mass modelling.Predicting orbits of artificial satellites, which rely on treating Earth as a centrally located point mass for most calculations.
Analysing binary star systems, where each star may be considered a point mass at the scale of their orbital separation.
These applications rely on the predictable nature of gravitational influence around spherical bodies, allowing meaningful calculations and comparisons.
Visual and Conceptual Benefits of Point-Mass Modelling
In addition to mathematical simplicity, representing spherical masses as points brings clarity to conceptual visualisation. Students can:
Understand gravitational fields through simple radial diagrams.
Relate field strength changes to distance from the centre.
Compare different masses easily using a single modelling framework.
Emphasising these advantages helps strengthen understanding of the broader gravitational-field topic and prepares learners for progressively more complex gravitational models involving potential, energy, and orbital mechanics.
FAQ
For a sphere, every mass element has an equivalent counterpart on the opposite side, allowing their gravitational effects to combine neatly into a single, centre-directed force. This balance collapses unless symmetry is perfect.
Irregular bodies lack this uniformity, meaning the gravitational field depends on the object's shape and distribution of mass. As a result, their external fields cannot be simplified to a single point without losing accuracy.
Even if density changes with depth, spherical symmetry is preserved as long as each layer is distributed evenly around the centre.
This means the gravitational contributions from each spherical shell combine to produce the same external field as a single point mass. Only the total mass and radius matter for external points, not the internal composition.
No. The point-mass approximation applies only outside the sphere.
Inside a uniform spherical body:
The gravitational field decreases linearly with distance from the centre.
Only the mass enclosed within the radius of interest contributes to the field.
Mass outside that radius has no net gravitational effect due to symmetry.
These differences break the point-mass equivalence internally.
Each mass element of the sphere exerts a force directed toward the centre. Symmetry ensures that horizontal components cancel, leaving only radial components.
Because every direction from the centre is equivalent, field lines must extend straight inwards. Any curvature would imply a preferred direction, which contradicts spherical symmetry.
Most planets are nearly spherical due to gravitational self-compression, but they do exhibit small deviations such as equatorial bulging caused by rotation.
For the majority of gravitational calculations—especially at distances much greater than the planet’s radius—these deviations are insignificant, and the point-mass model remains highly accurate.
However, for precise spacecraft navigation or measurements of gravitational anomalies, more detailed models are required.
Practice Questions
Question 1 (2 marks)
Explain why a spherically symmetric planet may be treated as a point mass when calculating the gravitational field at a point outside its surface.
Question 1 (2 marks)
1 mark: States that the mass distribution is spherically symmetric.
1 mark: States that, for points outside the sphere, the gravitational field behaves as though all mass is concentrated at the centre (i.e., equivalent to a point mass).
Question 2 (5 marks)
A planet has a spherically symmetric mass distribution.
(a) Describe what is meant by spherical symmetry.
(b) Explain why the gravitational influence of this planet at an external point is the same as if all its mass were concentrated at its centre.
(c) Discuss one practical application in physics or astronomy where this point-mass approximation is essential.
Question 2 (5 marks)
(a) Spherical symmetry (1 mark)
1 mark: States that the mass distribution depends only on distance from the centre / is identical in every radial direction.
(b) Why the planet behaves as a point mass (2 marks)
1 mark: Explains that contributions from all mass elements combine such that the net gravitational field at an external point acts towards the centre.
1 mark: States that the resulting field is identical to that produced by a single point mass located at the centre.
(c) Application (2 marks)
Award up to 2 marks for any valid application explained clearly:
1 mark: States an application where the point-mass approximation is used (e.g., calculating satellite orbits, planetary motion, gravitational field strength around Earth).
1 mark: Explains why the approximation is needed for that context (e.g., allows use of inverse-square law, simplifies orbital predictions, enables modelling of planets and moons as single masses).

