OCR Specification focus:
‘For a point mass, gravitational field strength is g = −GM/r² as a function of distance r.’
Gravitational field strength around a point mass describes how strongly a mass influences other objects at different distances, forming a foundational concept for understanding orbital motion and gravitational interactions.
Understanding Gravitational Field Strength Around a Point Mass
Gravitational fields communicate the attractive influence of mass. In the case of a point mass—an idealised object whose entire mass is considered concentrated at a single point in space—the field takes on a particularly simple and important mathematical form. This makes the point-mass model exceptionally useful for analysing stars, planets, moons, and even subatomic particles when their physical size is negligible compared with separation distances.
Nature of a Gravitational Field
A gravitational field describes the region surrounding a mass in which another mass experiences an attractive force. When dealing with large, spherically symmetric bodies such as Earth or stars, these objects can often be treated as point masses located at their centres, simplifying calculations and matching the formulation used in Newtonian gravitation.
Field Strength as a Radial Quantity
The gravitational field around a point mass is radial, meaning field lines point directly towards the mass. The magnitude decreases with increasing distance. This reflects the principle that the influence of a mass spreads out uniformly in all directions.
Defining Gravitational Field Strength
Gravitational field strength is a measure of how strongly a gravitational field acts on a unit mass placed within it. This makes it a central quantity in Newtonian gravitational theory, especially when considering how orbits and free fall arise from field behaviour.
Gravitational Field Strength: The force per unit mass experienced by a small test mass placed at a point in a gravitational field.
Because it is defined per unit mass, gravitational field strength is an inherent property of the field and not dependent on the mass used to probe it.
A gravitational field is always attractive, so its direction is towards the mass creating the field. This directionality is reflected in the sign convention used in the standard equation for point-mass gravitational fields.
The Point-Mass Gravitational Field Strength Equation
At the core of this subsubtopic is the inverse-square relationship between gravitational field strength and distance from a point mass. The specification emphasises the form:
g = −GM/r²
This expression relates how gravitational influence weakens with distance and depends on the mass sourcing the field.
EQUATION
—-----------------------------------------------------------------
Gravitational Field of a Point Mass (g) = −GM/r²
G = Universal gravitational constant (6.67 × 10⁻¹¹ N m² kg⁻²)
M = Mass of the gravitating object, in kilograms (kg)
r = Distance from the centre of mass to the point of interest, in metres (m)
—-----------------------------------------------------------------
The negative sign indicates that gravitational field vectors point towards the mass creating the field. This is consistent with the convention that inward radial directions are negative when chosen as such in coordinate systems.
The inverse-square dependence means that if the distance from a mass doubles, the field strength falls to one quarter of its original value.
Gravitational field lines around the Earth, treated as a spherically symmetric mass. The arrows show the field pointing radially inward, with line density indicating strength. This illustrates the radial, attractive nature of g as described by g = −GM/r². Source.
This feature governs everything from satellite orbits to the behaviour of comets and planetary atmospheres.
Conceptual Features of the Point-Mass Field
Understanding the characteristics of this field helps build intuition for gravitational interactions.
Radial Symmetry
Because the point mass creates a spherically symmetric field, every point at the same distance from the mass experiences identical field strength. This allows gravitational equipotential surfaces to be spherical and greatly simplifies the modelling of large astronomical bodies.
Dependence on Mass
The field strength is directly proportional to the mass generating the field. Larger masses produce proportionally stronger fields. This linearity is essential in astrophysics, where comparing gravitational fields of stars or planets is routine.
Dependence on Distance
The 1/r² dependence is fundamental. It implies:
Gravitational fields extend infinitely but weaken quickly
Most gravitational influence is concentrated close to massive objects
Orbits and free-fall trajectories are determined by distance-sensitive changes in field strength
Visualising Field Strength Around a Point Mass
Although not required to draw diagrams here, students benefit from understanding standard features of gravitational field-line diagrams for point masses:
Field lines point towards the mass, showing attraction
Lines become denser near the mass, representing stronger field strength
Line spacing increases with distance, illustrating decreasing magnitude
Symmetrical, radial distribution reflects the shape of the equation
These diagrams support the mathematical description and help visualise how objects respond to gravitational forces.
Practical and Theoretical Importance
The point-mass formulation is not merely theoretical. It underpins:
Orbital mechanics, where planets, moons, and satellites can be treated as point masses for many calculations
Free-fall near planets when distances are large compared with surface variations
Determining escape velocities and gravitational potential energy
Understanding the structure of galaxies and stellar systems
Key Observational Insights
Because gravitational fields weaken with distance, objects in orbit must move more slowly when farther from a central mass. This directly follows from the changing magnitude of g and forms the basis of Kepler’s laws, though those are covered in later subsubtopics.
Key Learning Points for OCR Students
To fully meet the specification, students should be able to:
State and interpret the equation g = −GM/r²
Understand that this form applies specifically to point masses and spherically symmetric bodies
Explain why the field is attractive and radial
Recognise the inverse-square relationship and its physical consequences
Connect field strength to gravitational force through F = mg, using the value of g from the point-mass formula
This content forms the mathematical and conceptual backbone of gravitational field analysis, supporting further study in orbital dynamics and gravitational potential.
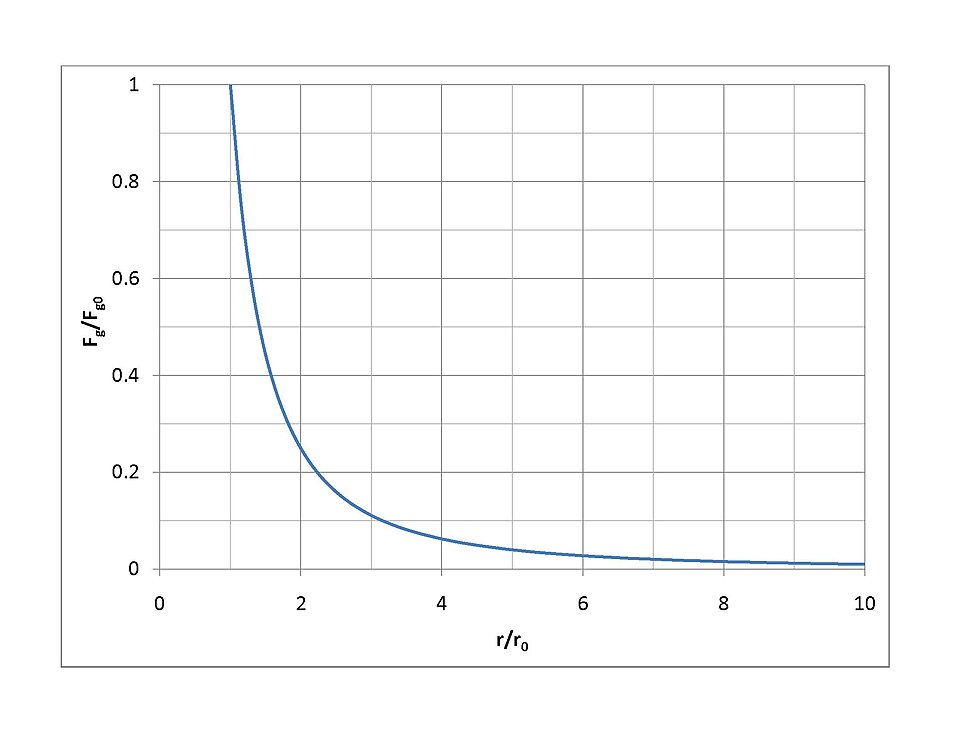
Graph showing how gravitational force — and thus gravitational field strength g — decreases with distance from a mass. The curve demonstrates inverse-square weakening, with much stronger fields close to the source. Axis values are illustrative and include extra detail not required by the syllabus. Source.
FAQ
The inverse-square law arises because a point mass emits its gravitational influence in all directions equally, spreading over the surface of an imaginary sphere centred on the mass.
As the radius of this sphere increases, its surface area grows proportionally to r².
Since the same gravitational influence must be spread over a larger area, the field strength at the surface reduces in proportion to 1/r².
This geometric reasoning applies to any field radiating uniformly from a point source.
No — the equation only applies outside a spherical mass or at its surface.
Inside a planet:
The gravitational field decreases linearly with distance from the centre (assuming uniform density).
Only the mass at smaller radii than the test point contributes to the gravitational pull.
At the exact centre, the contributions cancel in all directions, making g equal to zero.
There is no fixed size limit; the criterion depends on scale.
An object can be treated as a point mass when:
Its physical size is negligible compared with the distance between it and the point where g is calculated.
Variations in its shape or density have no meaningful effect on the gravitational field at that distance.
For example, a mountain-sized asteroid can be approximated as a point mass when calculating g tens of thousands of kilometres away.
If mass increases:
g increases proportionally, since g is directly proportional to M.
The shape of the field remains the same; only the magnitude changes at every point.
If r stays constant, any gradual increase in M causes a corresponding gradual increase in g at that location.
The radial dependence still follows g ∝ 1/r² at all times.
Yes — if two point masses exert equal and opposite gravitational pulls along the line joining them.
A point of zero net field (a neutral point) occurs where:
The gravitational pull from one mass equals the pull from the other.
The point lies closer to the smaller mass, because the larger mass produces stronger gravitational influence.
This concept underlies equilibrium points in multi-body gravitational systems, although full treatment of such systems lies beyond the scope of this subsubtopic.
Practice Questions
(2 marks)
A spacecraft is at a distance r from a planet of mass M. State the equation for the gravitational field strength g at this point and explain the meaning of the negative sign.
Question 1 (2 marks)
1 mark: States g = −GM/r².
1 mark: Explains that the negative sign shows the field (and force) is directed towards the mass/attractive/inwards.
(5 marks)
A planet may be approximated as a point mass. A probe is sent to study this planet and moves directly away from its centre.
(a) Describe how the gravitational field strength varies with distance from the planet.
(b) Explain why modelling the planet as a point mass is appropriate and how this affects the calculation of g.
(c) State two consequences of the inverse-square dependence of g on the motion of objects in the planet’s gravitational field.
Question 2 (5 marks)
(a) 2 marks:
1 mark: States that gravitational field strength decreases with increasing distance.
1 mark: States that the relationship follows an inverse-square law / proportional to 1/r².
(b) 2 marks:
1 mark: Explains that a spherically symmetric planet can be modelled as if all its mass acts at its centre.
1 mark: States that this simplifies calculation of g using g = −GM/r².
(c) 1 mark:
Any two of the following (1 mark total for two correct statements):
Objects experience much stronger gravitational effects when close to the planet.
Orbital or escape velocities decrease with increasing distance.
Small changes in distance close to the surface cause significant changes in g.
Motion (e.g., orbits or trajectories) becomes less curved/weaker gravitational influence at large distances.

