OCR Specification focus:
‘Close to Earth’s surface, g is approximately uniform and equals the free-fall acceleration.’
Near Earth’s surface, the gravitational field can be treated as uniform, allowing simplified analysis of motion and forces. This approximation underpins many standard results used in physics.
The Nature of the Uniform Gravitational Field Near Earth’s Surface
Close to the Earth, the gravitational field behaves in a way that allows us to assume its strength is effectively constant. This assumption forms the foundation of many models used in mechanics, especially those involving falling objects or projectiles. Although the Earth’s gravitational field is truly radial and decreases with altitude, the change is extremely small over the heights encountered in everyday situations, enabling the adoption of a simplified uniform-field model.
Why the Field Appears Uniform
The idea of a uniform gravitational field refers to a region in which the gravitational field strength has the same magnitude and direction at all points. Since the radius of Earth is large compared with typical distances above the surface, the variation in g is negligible for most practical purposes. Because of this, gravitational field lines within this region can be drawn as parallel and evenly spaced, representing a constant field strength directed toward Earth’s centre.
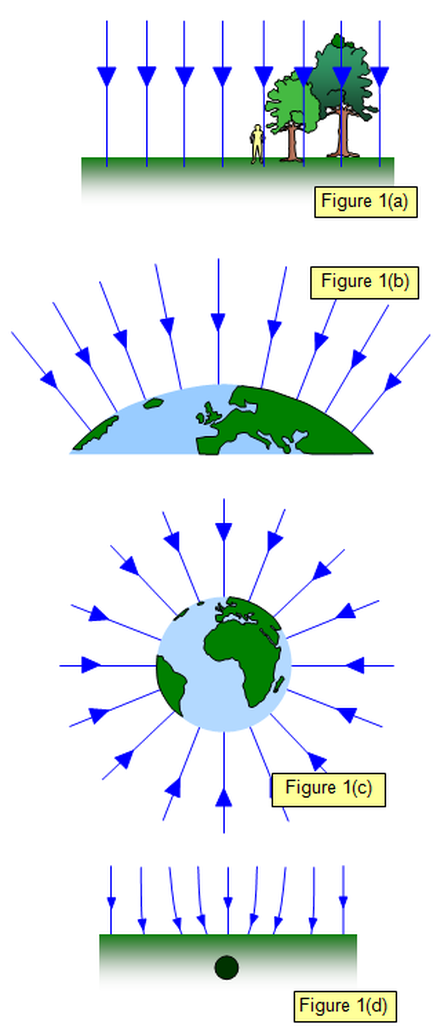
A set of panels compares the near-surface parallel gravitational field lines with the global radial field around Earth. The local uniform region illustrates why g is treated as constant. Additional panels showing geological variations exceed the needs of this subsubtopic. Source.
Gravitational field strength: The force per unit mass experienced by a small test mass placed in a gravitational field.
This constancy of gravitational field strength means that the free-fall acceleration for objects near the Earth’s surface is also constant, justifying the specification statement that g is approximately uniform and equals the free-fall acceleration. This directly supports the commonly used value of 9.81 m s⁻², although rounded values such as 9.8 m s⁻² are often acceptable for calculations.
A uniform field allows physics problems to be tackled using simplified models, but it is important for students to recognise the assumptions and limits of the approximation.
Gravitational Field Strength in a Uniform Region
In a uniform gravitational field, the magnitude of g does not vary with height. The force acting on a mass in this region therefore follows a predictable pattern, enabling direct proportionality between weight and mass.
EQUATION
—-----------------------------------------------------------------
Weight (W) = mg
W = Weight, the gravitational force acting on an object (newton, N)
m = Mass of the object (kilogram, kg)
g = Gravitational field strength or free-fall acceleration (metre per second squared, m s⁻²)
—-----------------------------------------------------------------
Because g is constant in this model, the direction of motion for a freely falling object remains unchanged until another force intervenes. This makes the uniform-field approximation extremely useful in analysing vertical motion without air resistance.
The simplicity of the relationship between mass and weight in a uniform field also provides an intuitive interpretation of gravitational effects. Students should recognise how this contrasts with situations involving significant changes in altitude, where g no longer remains constant and more general gravitational laws must be applied.
Representing the Uniform Gravitational Field
Gravitational fields may be illustrated using field lines to represent both the direction and strength of the field. In the uniform region near the surface, these lines convey helpful visual information about how gravity acts.
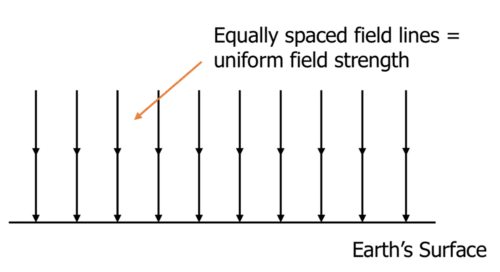
This clean schematic shows a uniform gravitational field represented by identical downward arrows above Earth’s surface. It reinforces the concept of constant magnitude and direction for g near the surface. Other contextual material on the page relates to general field problems and is not required here. Source.
Features of Gravitational Field Lines in a Uniform Field
Field lines for a uniform gravitational field:
Are parallel, indicating that the direction of gravitational force is identical at all points.
Are equally spaced, showing that the gravitational field strength remains constant throughout the region.
Point vertically downward, as the local direction toward Earth’s centre is effectively the same across small surface-adjacent regions.
Become a useful tool for visualising how objects respond to gravitational forces in simplified models.
These characteristics reinforce the conceptual difference between the uniform field near the surface and the radial field surrounding a point or spherical mass. In the latter, field lines diverge, and their spacing increases with distance, reflecting the inverse-square nature of the field.
Applications of the Uniform-Field Approximation
A wide range of introductory and intermediate mechanics relies on the assumption of a uniform gravitational field. This assumption is not merely for convenience; within its valid range, it closely matches the real behaviour of gravitational acceleration at typical altitudes.
Key Situations Where the Approximation is Applied
Students will encounter uniform-field modelling in multiple contexts:
Free-fall motion, where objects accelerate downward at constant g.
Vertical projection, both upwards and downwards, analysed using constant-acceleration equations.
Projectile motion, in which the horizontal and vertical motions are treated independently, with the vertical acceleration taken as g.
Weight and equilibrium problems, where constant gravitational force provides a steady vertical load on structures or objects.
Energy calculations, where changes in gravitational potential energy simplify to mgh only when g remains constant.
Each of these applications relies on the assumption that g does not vary significantly over the distances involved.
Limitations of the Uniform-Field Model
While the uniform-field approximation is powerful, students must be able to identify its limitations. The approximation breaks down when the heights under consideration become large relative to Earth’s radius. At substantial altitudes, the gravitational field strength decreases, field lines begin to diverge noticeably, and the simpler model no longer holds.
Situations such as satellite motion, orbital calculations, and gravitational interactions beyond the near-surface region require the more general inverse-square law of gravitation rather than the simplified uniform field approach.
FAQ
Over small height changes such as climbing a building, the change in g is extremely small. For example, at 100 m above the surface, g decreases by only about 0.003 m s⁻².
This change is far below what humans can detect without instruments, which is why g is treated as constant in typical near-surface situations.
Field lines are drawn as parallel because, over tiny regions compared with Earth’s radius, the curvature of the planet is negligible. This means:
• The direction toward the centre of Earth changes by an imperceptibly small angle.
• The spacing between field lines barely alters across regions a few kilometres wide.
This approximation fails only when considering distances large enough that Earth’s curvature becomes noticeable.
For school-lab distances, the approximation has almost no measurable impact. Deviations from constant g are far smaller than typical human or equipment uncertainties.
The biggest sources of error in timing free fall are reaction times, air resistance, and imperfect release mechanisms, not changes in gravitational field strength.
Gravitational force is proportional to mass, but acceleration depends on force divided by mass. These effects cancel, so:
• Heavier objects experience a larger gravitational force.
• But they also have proportionally more inertia.
This results in the same acceleration for all freely falling bodies, provided air resistance is negligible.
For most practical purposes, the approximation holds within the first few kilometres above the surface. Even at altitudes of several thousand metres, g has only decreased by a small fraction.
For aviation altitudes and above, the reduction becomes more noticeable, and calculations involving varying g or the inverse-square law become more appropriate.
Practice Questions
Question 1 (2 marks)
Explain why the gravitational field near Earth’s surface can be treated as uniform. In your answer, refer to the behaviour of gravitational field lines.
Question 1 (2 marks)
• Field lines are parallel and evenly spaced close to the surface. (1)
• This indicates that both the direction and magnitude of the gravitational field strength remain nearly constant. (1)
Question 2 (5 marks)
A small object is released from rest near Earth’s surface.
(a) State the approximate value of the free-fall acceleration.
(b) Explain why this value is considered constant for objects falling small distances above the surface.
(c) Describe how the motion of the object would differ if the gravitational field were not uniform.
Question 2 (5 marks)
(a) Free-fall acceleration is approximately 9.8 m s⁻² or 9.81 m s⁻². (1)
(b)
• Earth’s radius is very large compared with small height changes near the surface. (1)
• Therefore the change in gravitational field strength with height is negligible, so g is treated as constant. (1)
(c)
• If the field were not uniform, g would change with height. (1)
• The object’s acceleration would vary during the fall, so its motion would not follow constant-acceleration equations. (1)

