OCR Specification focus:
‘State and use Kepler’s three empirical laws describing planetary motion around the Sun.’
Kepler’s three laws describe how planets move around the Sun, revealing predictable patterns in orbital shape, motion, and timing. These empirical laws underpin Newtonian gravitational theory.
Kepler’s First Law: The Law of Orbits
Kepler’s first law states that a planet moves in an elliptical orbit with the Sun at one focus.
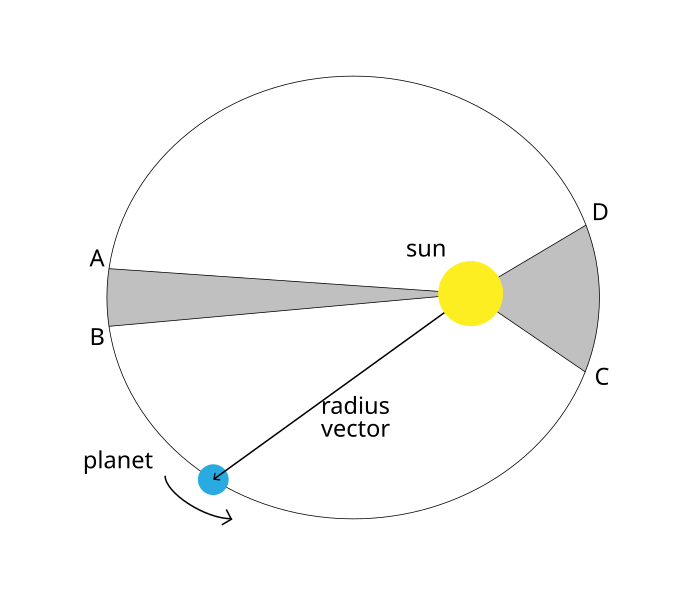
This diagram shows an elliptical orbit with two shaded regions of equal area swept out in equal time intervals, illustrating Kepler’s second law. Although placed here after the first law sentence as instructed, the diagram remains relevant for understanding how orbital geometry affects motion. Source.
This was historically significant because it replaced the long-held assumption of circular orbits and provided a more accurate mathematical description of planetary paths.
Understanding Elliptical Orbits
Planets rarely move in perfect circles; instead, they follow ellipses of varying eccentricity.
An ellipse is a closed curve in which the total distance from any point on the curve to the two foci is constant.
The eccentricity measures how stretched the ellipse is; values range from 0 (a perfect circle) to close to 1 (highly elongated).
For the Solar System, most planetary eccentricities are low, meaning their orbits are nearly circular but still fundamentally elliptical.
Ellipse: A closed curve for which the sum of the distances from any point on the curve to two fixed points (the foci) is constant.
Because the Sun occupies one focus rather than the centre, a planet’s distance from the Sun changes continuously along its orbit. This radial variation influences the planet’s speed and contributes to the structure of Kepler’s second law.
Kepler’s Second Law: The Law of Areas
Kepler’s second law states that a line joining a planet to the Sun sweeps out equal areas in equal time intervals.
This describes how orbital speed varies: planets move faster when closer to the Sun and slower when farther away.
Geometric Interpretation
The law is fundamentally a geometric relationship.
Imagine slicing a planet’s orbit into time intervals of equal length.
The sectors formed by the radius vector (planet–Sun line) have equal area.
When the planet is near perihelion — its closest point to the Sun — it must move faster to sweep out an area equal to the slower motion near aphelion, the furthest point.
This demonstrates a deep link between planetary speed and separation, later explained by Newtonian gravitational and conservation laws.
Perihelion: The point in a planet’s orbit where it is closest to the Sun.
A key insight is that variable orbital speed does not violate the regularity of orbital periods, which is addressed by Kepler’s third law in a broader, quantitative way.
Kepler’s Third Law: The Law of Periods
Kepler’s third law provides a mathematical relationship between a planet’s orbital period and the radius of its orbit. For planets orbiting the Sun, the law states that the square of the orbital period is proportional to the cube of the mean orbital radius.
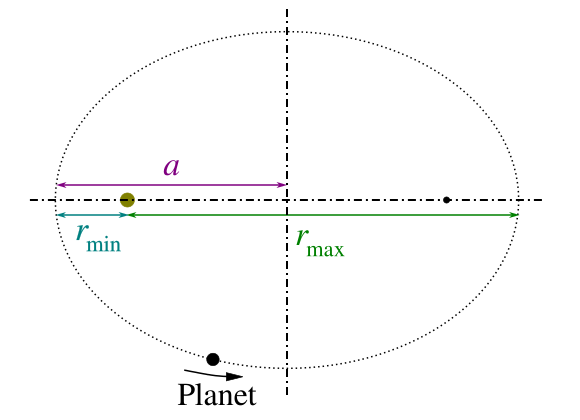
This diagram illustrates an elliptical orbit with labelled axes and the relationship T² ∝ a³, summarising Kepler’s third law. It highlights the dependence of orbital period on the semi-major axis. The axis labels go slightly beyond the specification but clearly enhance understanding of how orbital geometry relates to timing. Source.
Quantitative Statement of the Law
For Solar System planets:
If the orbital radius increases, the orbital period increases significantly more.
This proportionality is universal for bodies orbiting the same central mass, making the law exceptionally useful for comparing orbits within a system.
EQUATION
—-----------------------------------------------------------------
Kepler’s Third Law (T²–r³ relation) = T² ∝ r³
T = Orbital period of the planet in seconds
r = Mean orbital radius or semi-major axis in metres
—-----------------------------------------------------------------
The equation shows that the ratio T²/r³ is constant for all planets orbiting the Sun. This constant depends on the mass of the Sun and later connects directly to Newton’s law of gravitation. The relationship applies strictly to elliptical orbits when r is taken as the semi-major axis.
Why the Law Matters
Kepler’s third law is particularly useful for:
Comparing the relative orbital speeds and distances of different planets.
Predicting orbital periods for newly discovered objects, provided the orbital radius is known.
Establishing a quantitative framework that Newton later generalised to any two bodies attracting each other gravitationally.
After Kepler, Newton demonstrated that the three laws emerge naturally from gravitational attraction obeying an inverse-square law and from classical mechanics. Although students studying this subsubtopic focus solely on Kepler’s laws themselves, it is helpful to appreciate that these empirical laws became foundational evidence for Newton’s theoretical work.
Applying Kepler’s Three Laws
To understand and use these laws effectively, students should be able to:
Identify elliptical orbital features such as foci, perihelion, and aphelion.
Relate changes in orbital speed to radial position using the equal-areas principle.
Use the proportional form of Kepler’s third law to compare or predict orbital periods.
Key points to remember:
Kepler’s first law describes the shape of the orbit.
Kepler’s second law describes how speed varies along the orbit.
Kepler’s third law links the timing of the orbit to its size.
These three connected insights form the essential framework for describing planetary motion under gravitational influence.
FAQ
Kepler derived his laws empirically by analysing detailed planetary observations recorded by Tycho Brahe. He compared predicted circular orbits with actual data and found persistent discrepancies.
Through repeated geometric modelling, he identified ellipses as the only orbital shape that fit Mars’ observed motion.
His second and third laws emerged from studying how fast Mars must travel at different points and comparing orbital periods across planets.
Low eccentricities arise because the Solar System formed from a rotating disc of gas and dust, which naturally produced near-circular orbits. Collisions and interactions damped radial motions over time.
Highly eccentric orbits do occur, but they are more common among comets and small bodies affected by gravitational encounters.
Large planets tend to retain near-circular orbits because their greater mass stabilises them against disturbances.
Kepler’s second law follows from conservation of angular momentum. As a planet moves closer to the Sun, gravitational attraction increases its tangential speed so that its angular momentum remains constant.
This produces:
Higher speed near perihelion
Lower speed near aphelion
Although Kepler discovered the pattern first, Newton’s laws later provided the theoretical explanation.
Yes, provided the central mass dominates the system. The law generalises to any two bodies where one mass is much larger than the other.
For moons, the constant T²/r³ differs from the Solar System value because it depends on the mass of the central body.
Each planet–moon system has its own constant determined by that planet’s mass.
The semi-major axis is half the longest diameter of the ellipse, and it effectively measures the orbital “size”.
It is not the average of the minimum and maximum distances but is closely related to the orbital energy:
Larger semi-major axis → higher orbital energy and longer period
Smaller semi-major axis → lower orbital energy and shorter period
Kepler’s third law uses the semi-major axis because it remains constant even though the planet–Sun distance changes throughout the orbit.
Practice Questions
Question 1 (2 marks)
State Kepler’s first and second laws of planetary motion.
Question 1 (2 marks)
1 mark: Kepler’s first law — planets move in elliptical orbits with the Sun (or star) at one focus.
1 mark: Kepler’s second law — a line joining a planet to the Sun sweeps out equal areas in equal time intervals.
Question 2 (5 marks)
A newly discovered exoplanet orbits its star in an elliptical orbit.
(a) Describe how the planet’s speed changes during its orbit, referring to Kepler’s laws.
(b) Explain how Kepler’s third law allows astronomers to estimate the orbital period of this exoplanet if they can determine its mean orbital radius.
(c) State one assumption that must be made when applying Kepler’s third law to this system.
Question 2 (5 marks)
(a)
1 mark: Planet moves faster when closer to the star (near perihelion).
1 mark: Planet moves slower when further from the star (near aphelion).
(b)
1 mark: Kepler’s third law states that the square of the orbital period is proportional to the cube of the mean orbital radius.
1 mark: Knowing the orbital radius allows the orbital period to be calculated or estimated using the proportionality T² ∝ r³.
(c)
1 mark: Assume the star’s mass is much larger than the planet’s / the planet’s mass is negligible compared with the star / the orbit is dominated by a single central mass.

