OCR Specification focus:
‘For planets, the necessary centripetal force is provided by the Sun’s gravitational attraction.’
Planetary motion arises because a planet continually accelerates towards the Sun under gravity, causing its path to curve into an orbit rather than continuing in a straight line through space.
Gravity as the Source of Centripetal Force
In circular or near-circular planetary orbits, the inward force required to maintain the curved path is known as the centripetal force.
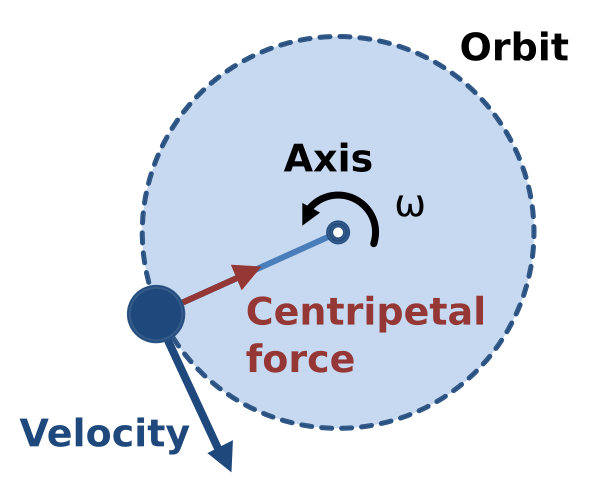
A body moves in a circular path while an inward centripetal force acts towards the centre, perpendicular to its tangential velocity. The diagram highlights how the force direction constantly changes the direction of motion while the speed can remain constant. This generic circular-motion model underpins the later idea that gravity can serve as the centripetal force in orbital motion. Source.
This force is always directed towards the centre of the orbit. For a planet orbiting a star, the centripetal force is provided entirely by gravitational attraction, meaning that the dynamics of orbital motion can be understood through the interaction of mass, distance, and gravitational field strength.
Because gravitational interaction acts along the line joining the centres of two masses, it supplies exactly the central inward pull required to keep a planet in orbit.
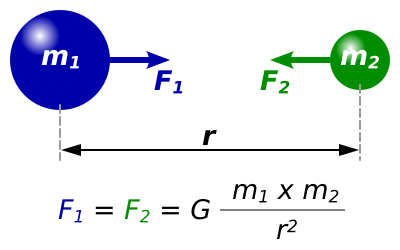
Two point masses attract each other with equal and opposite gravitational forces directed along the line connecting them. The distance r and Newton’s law of universal gravitation are clearly labelled, illustrating how gravity provides the central force necessary for orbital motion. The inclusion of the constant G provides extra detail but supports the understanding of gravitational centripetal force. Source.
Without this force, the planet would move in uniform straight-line motion according to Newton’s first law.
Centripetal Force: The inward force required to keep an object moving in a circular path at constant speed.
The gravitational attraction between two bodies is always mutual. The Sun pulls on a planet, providing the centripetal force for the planet’s orbit, while the planet pulls back on the Sun with equal magnitude. However, because the Sun is so massive, its resulting acceleration is extremely small.
Newtonian Gravitation and Orbital Motion
The combination of Newton’s law of gravitation and Newton’s laws of motion forms the basis for explaining why gravity supplies the centripetal force in orbital systems. When the gravitational force equals the centripetal requirement for circular motion, a stable orbit can be maintained. This relationship links orbital speed, radius, and the masses involved.
EQUATION
—-----------------------------------------------------------------
Gravitational Force (F) = GMm / r²
G = Gravitational constant, 6.67 × 10⁻¹¹ N m² kg⁻²
M = Mass of central body (kg)
m = Mass of orbiting body (kg)
r = Distance between centres of the two bodies (m)
—-----------------------------------------------------------------
A planet in circular motion also requires a centripetal force:
EQUATION
—-----------------------------------------------------------------
Centripetal Force (F) = mv² / r
m = Mass of orbiting body (kg)
v = Orbital speed of the body (m s⁻¹)
r = Orbital radius, measured to the centre of the circular path (m)
—-----------------------------------------------------------------
When gravitational force provides the centripetal force, these expressions are equal. Although the process of equating them is part of standard orbital derivations, students do not need to calculate full solutions here. Instead, the key conceptual point is that the gravitational attraction automatically supplies the precise inward force needed for the observed orbital motion.
Why Gravity Produces Centripetal Acceleration
Gravity produces centripetal acceleration, not because it changes the planet’s speed significantly, but because it continually redirects the planet’s velocity towards the centre of its orbit. This redirection constitutes acceleration, even if the orbital speed remains constant.
Key ideas:
The velocity of an orbiting body is always tangential to its path.
The gravitational force is always radial, pointing towards the central mass.
These perpendicular directions ensure that gravity changes direction, not magnitude, of velocity in circular motion.
The result is a stable orbit where the planet continually “falls” towards the Sun but never reaches it.
Relating Orbital Radius and Speed
The balance between gravitational force and centripetal force underpins the predictable relationship between orbital radius and orbital speed. This relationship explains why planets farther from the Sun orbit more slowly. Since gravity weakens with increasing distance, the required centripetal force decreases, so only a lower orbital speed is necessary to maintain a stable orbit.
Seen from above the ecliptic, this diagram shows the elliptical orbits of the outer planets around the Sun. It illustrates how orbital radius relates to the gravitational force needed for stable motion, connecting real planetary paths with centripetal-force concepts. The perihelion, aphelion, and orbital-node markers add extra astronomical detail while remaining consistent with the physics of gravitationally governed orbits. Source.
Orbital Radius: The distance from the centre of the central mass to the centre of the orbiting body, governing both orbital speed and gravitational attraction.
This interplay forms the foundation of orbital mechanics and links directly to Kepler’s findings about planetary periods. Although Kepler’s third law is handled in a different subsubtopic, the principle here remains: gravitational attraction determines orbital motion.
Features of Orbits Governed by Gravitational Centripetal Force
The concept of gravity providing centripetal force applies not only to planets but also to moons, artificial satellites, and stars orbiting galactic centres. The same physical principles operate across all scales.
Important characteristics:
Direction of force: Always towards the central mass.
Magnitude of force: Depends on both masses and the inverse square of distance.
Type of motion produced: Uniform circular motion for constant speed and radius; elliptical motion when speed and distance vary but gravitational attraction remains the inward force.
Energy considerations: Even when gravity supplies centripetal force, the total mechanical energy of an orbit remains constant unless external forces act.
Independence from mass of orbiting body: The orbiting body’s mass appears on both sides of the centripetal–gravitational balance, so its value does not affect the size of orbit for a given speed.
Using Gravity as the Centripetal Force in Analysis
In A-Level Physics, recognising gravity as the source of centripetal force allows students to:
Understand the mechanics of natural orbital systems.
Predict how changes in orbital radius affect required orbital speed.
Analyse satellite motion using gravitational principles.
Link gravitational fields to planetary and astrophysical dynamics.
These points ensure that the modelling of orbital systems remains consistent with Newtonian principles and with the OCR requirement that gravitational attraction supplies the centripetal force for planetary orbits.
FAQ
A centripetal force acts at right angles to the direction of motion. Because it is perpendicular, it changes only the direction of the velocity, not its magnitude.
This means kinetic energy remains constant in a perfectly circular orbit. Any speed changes in real planetary orbits arise from elliptical motion, not from the nature of the centripetal force itself.
Gravity decreases naturally with distance. A planet settles into an orbital radius where its speed and the gravitational pull match the condition for circular motion.
If the orbit is too close, gravitational force becomes too strong and accelerates the planet outward into a wider orbit; if too far, gravitational pull is too weak and the planet drifts inward. This creates a self-correcting balance.
The inward force changes direction, not speed, so the planet does not lose kinetic energy.
Planets would spiral in only if energy were continually removed from the system. In space, frictional forces are negligible, so orbits remain stable for extremely long times.
A short disturbance typically shifts the orbit into a slightly elliptical shape rather than destroying it.
Key outcomes include:
The planet moves faster when closer to the star.
The centripetal force requirement varies with distance, but gravity remains the inward force.
The orbit remains bounded unless the disturbance raises the energy above escape energy.
When masses are comparable, both bodies orbit a common centre of mass rather than one orbiting a fixed central object.
This leads to:
A noticeable wobble of both bodies.
A centripetal force acting on each body due to mutual gravitational attraction.
A shared orbital path whose shape depends on the mass ratio and separation.
Practice Questions
Question 1 (3 marks)
A planet orbits a star in a nearly circular orbit. Explain why a centripetal force is required for this motion and identify the force that provides it.
Question 1 (3 marks)
1 mark: States that circular motion requires an inward (centripetal) force to continuously change the direction of velocity.
1 mark: Explains that without this force, the planet would move in a straight line at constant speed (Newton’s first law).
1 mark: Identifies gravity (gravitational attraction from the star) as the force providing the centripetal force.
Question 2 (6 marks)
A small moon orbits a planet in a circular path of radius r.
(a) State the condition that must be met for the moon to remain in circular orbit.
(b) Explain how gravitational attraction produces the centripetal acceleration of the moon.
(c) Using your explanation, discuss how the orbital speed of the moon would change if the orbital radius increased.
Question 2 (6 marks)
(a)
1 mark: States that centripetal force must equal gravitational force for circular orbit (or equivalent: inward force equals mv²/r).
(b)
1 mark: States that gravitational force acts along the line joining the centres of the two bodies.
1 mark: Explains that this force is directed towards the planet, providing the required inward (centripetal) force.
1 mark: Explains that this causes centripetal acceleration by constantly changing the direction of the moon’s velocity.
(c)
1 mark: States that gravitational force decreases with increasing orbital radius.
1 mark: States that a lower centripetal force is required at larger radii for circular orbit, so orbital speed decreases.

