Planetary and satellite motion relies on the predictable relationship between orbital period and orbital radius, showing how Newtonian gravitation determines the timing, stability, and scale of circular orbits.

The Orbital Period–Radius Relationship

The orbital period–radius relation describes how the time taken for an object to complete one circular orbit depends on its distance from the central mass generating the gravitational field. This subsubtopic extends Newton’s law of gravitation by combining it with uniform circular motion, producing a powerful predictive equation essential for analysing planetary systems, satellites, and astrophysical contexts. The specification emphasises using the relation
T² = (4π²/GM) r³
and understanding its derivation from fundamental physical principles.

Linking Gravitational and Centripetal Forces

A body in a circular orbit is constantly accelerating towards the centre of the orbiting path. This acceleration is supplied by the gravitational force. As a result, a key conceptual focus is recognising how gravitational attraction provides the centripetal force needed for circular motion.

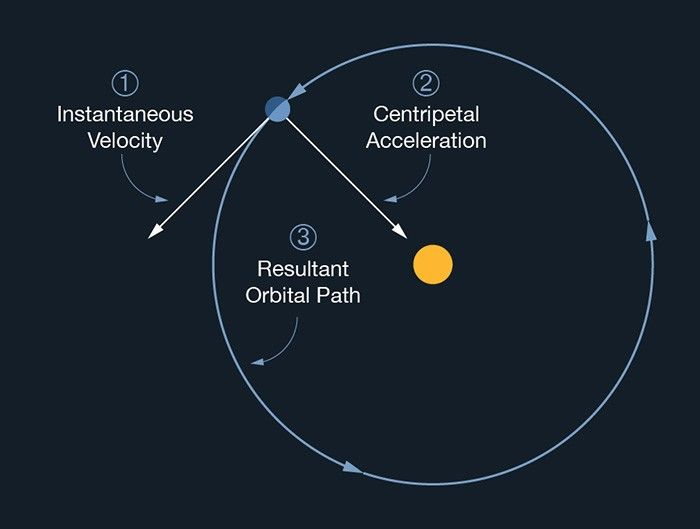
A body in uniform circular orbit around a central mass. Tangential velocity carries the object forward while the inward centripetal acceleration bends its path, illustrating gravity’s role in sustaining circular motion. Source.

Once this equivalence between forces is established, students can appreciate that orbital motion is not separate from Newtonian mechanics but rather a direct consequence of it. The gravitational interaction dictates both the speed of orbital motion and the period required to complete one revolution.

A planet or satellite remains in orbit because its tangential velocity is exactly sufficient for the curved path to match the curvature of the gravitational potential. This balance ensures the object continues “falling around” the central body rather than crashing into it or escaping entirely.

Deriving the Period–Radius Equation

To arrive at the orbital period–radius relation, gravitational force is equated with the expression for the centripetal force required for circular motion. The gravitational force between a planet (mass m) and a much larger central mass M is set equal to the centripetal force needed to keep the smaller body in orbit. From this, the orbital speed can be related to the radius of the orbit and then rearranged in terms of the orbital period T.

EQUATION
—-----------------------------------------------------------------
Orbital Period–Radius Relation (T² = (4π²/GM) r³) = T² = (4π²/GM) r³
T = Orbital period in seconds (s)
G = Universal gravitational constant in N m² kg⁻²
M = Mass of central body in kilograms (kg)
r = Orbital radius measured from the centre of mass in metres (m)
—-----------------------------------------------------------------

This equation shows that the square of the orbital period is directly proportional to the cube of the orbital radius. It forms the Newtonian basis for Kepler’s third law, although the OCR specification treats Kepler’s laws elsewhere.

Features and Implications of the T²–r³ Relationship

The relationship enables learners to understand several key properties of orbital systems:

• Larger orbits correspond to dramatically longer orbital periods because increasing r slightly causes a much larger increase in r³.

• Mass of the central body strongly influences orbital dynamics, with larger M producing shorter orbital periods for a given radius because the gravitational field is stronger.

• The mass of the orbiting body does not appear in the equation, indicating that all objects at the same radius orbit with the same period, assuming negligible additional forces.

• Circular orbits are assumed, meaning the relationship applies cleanly when eccentricity is low.

• Applicable across planetary, lunar, and artificial satellite systems, as long as gravitational interaction dominates other forces.

These points demonstrate why the relation is used extensively in astronomy and satellite engineering, including calculating the location of operational orbits, predicting motion in multi-body systems, and assessing stability.

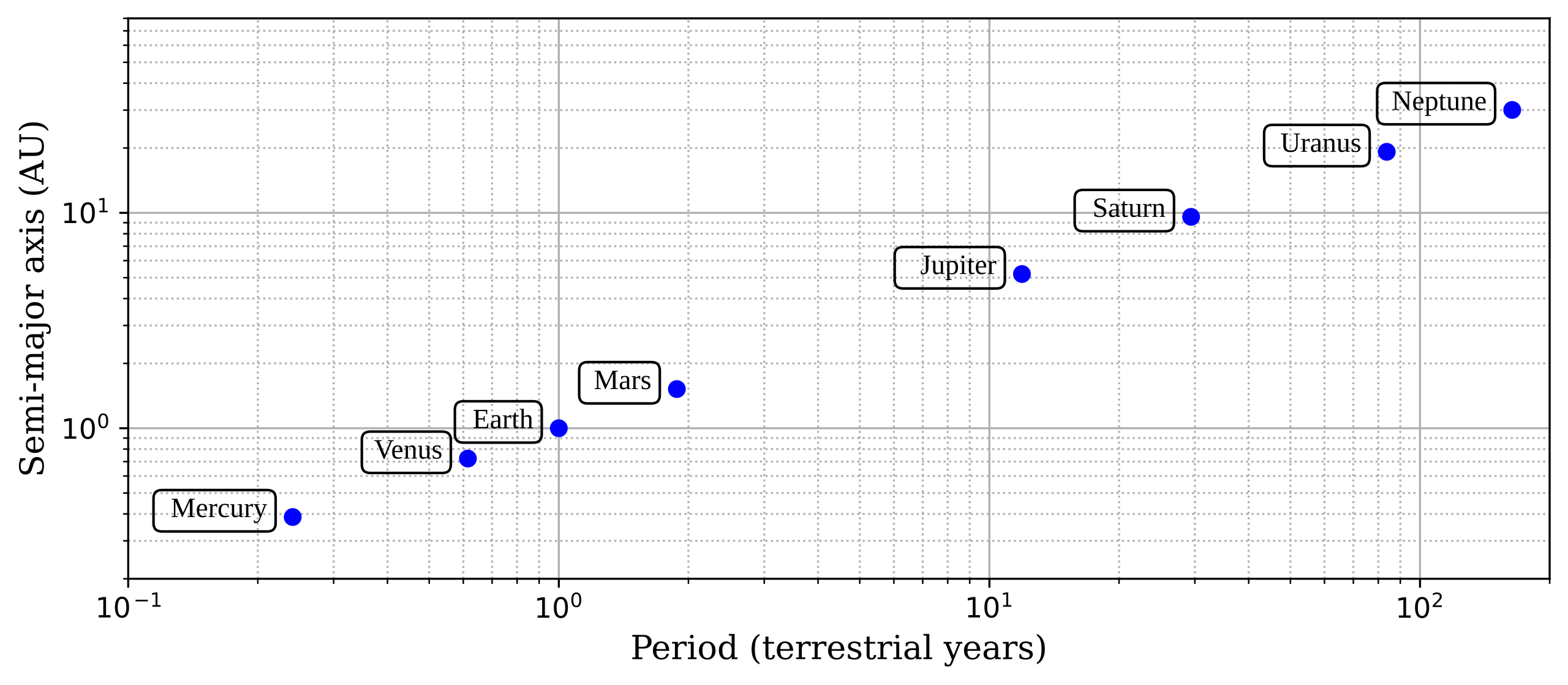
Log–log plot of orbital period versus semi-major axis for the eight planets. The near-linear distribution illustrates the proportionality between T2T²T2 and r3r³r3. The logarithmic scales and use of AU/years add additional context beyond the OCR requirement but help highlight the power-law relationship. Source.

Physical Interpretation of the Equation

The proportionality between T² and r³ expresses a fundamental characteristic of gravitational fields governed by an inverse-square law. By comparing how gravitational force weakens with distance, students see that the decrease in force necessitates lower orbital speed at larger radii. Lower speeds lead to increased time to complete a full orbit, which becomes especially significant at very large distances.

After defining this term, it is useful to consider how the constant 4π²/GM controls the steepness of the T²–r³ curve. Because M is in the denominator, a massive central body creates a shallower slope, showing that periods rise more slowly with increasing radius.

Between Earth and the Sun, for example, orbital periods rise predictably with radius in a way that remains consistent with this principle. This universality means that analysing distant planetary systems, calculating orbital timings for missions, or designing satellite constellations all rely on the same underlying physics.

Using the Orbital Period–Radius Relation

This relation is both descriptive and predictive. Within the OCR A-Level context, emphasis falls on its mathematical form and physical basis. Students must recognise how observations of orbital periods can reveal unknown masses, distances, or gravitational properties.

When applying the equation, learners should note:

• It assumes Newtonian gravity; relativistic corrections are unnecessary at A-Level.

• It requires circular orbits; however, it provides a good approximation for mildly elliptical orbits by treating r as the semi-major axis.

• It allows identification of central mass M if T and r are known, an essential tool in astrophysics.

• It reinforces the concept that gravitational interactions alone govern orbital dynamics in a two-body approximation.

Mastery of the orbital period–radius relation gives students a rigorous foundation for the broader topic of planetary motion, ensuring that they can apply Newtonian gravitation to real orbital systems with confidence and precision.