Kepler’s third law provides a powerful and universal relationship between an orbiting body’s period and its orbital radius, enabling prediction and comparison of motion across diverse astronomical systems.

Understanding Kepler’s Third Law in General Contexts

Kepler’s third law originally described the motion of planets around the Sun, but its power extends far beyond the Solar System. The law states that the square of the orbital period of a body is proportional to the cube of its orbital radius, a relationship that emerges naturally from Newton’s law of gravitation and the dynamics of circular or near-circular motion. This proportionality holds for any gravitationally bound two-body system, provided one mass is significantly larger than the other. As a result, the law applies equally well to exoplanets, moons, and artificial satellites in stable orbits.

Universal Application of the Period–Radius Relationship

For OCR A-Level Physics, you must recognise that Kepler’s third law is not confined to one specific set of bodies. Instead, the proportionality T² ∝ r³ is a general result of gravitational interactions. In such systems, the central mass determines the gravitational field, and any smaller body in orbit must move with a speed that provides the required centripetal force. The balance of forces creates the familiar relation between period and radius, enabling astronomers and physicists to determine orbital parameters across the universe.

Although different systems may vary in mass, distance, and complexity, the underlying law retains its form. This universality is crucial for interpreting observational data from modern astronomy, particularly where direct measurement of orbital parameters is challenging.

Derivation Context and Importance

Students are expected to understand that the commonly used form
T² = (4π²/GM) r³
arises from combining Newtonian gravitation with circular motion. However, the OCR specification emphasises the ability to apply the proportionality rather than to re-derive it for unfamiliar systems. The essential idea is that a larger orbital radius leads to a longer period, and this relationship remains constant within a given system because the central mass M is fixed for all orbiting bodies.

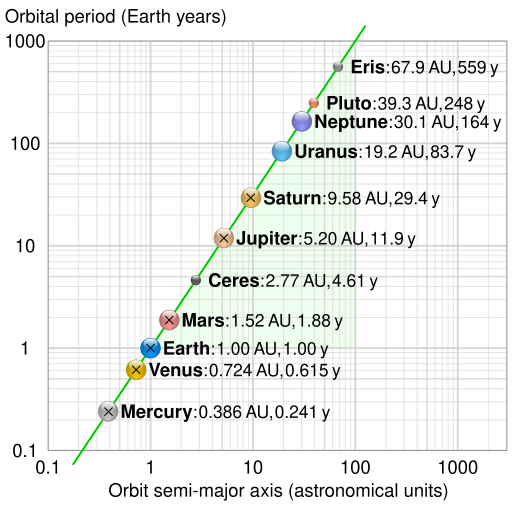
A log–log plot showing the orbital periods and semimajor axes of Solar System bodies. The straight-line trend demonstrates Kepler’s third law in action for bodies orbiting the Sun. Some additional bodies and historical data are included beyond the OCR requirement but support the same proportionality. Source.

Key Features of the General Law

Applying Kepler’s third law beyond the Solar System requires clear understanding of its assumptions and limitations. The following features shape its use in broader astrophysical contexts:

• The law assumes a dominant central mass, meaning the orbiting body’s mass is negligible in comparison.

• The orbit should be approximately circular or treated as if circular (using the semi-major axis for elliptical orbits).

• The gravitational influence of additional bodies must be small enough not to disturb the regular orbital motion.

• The proportionality constant depends on the gravitational parameter GM of the central body.

These conditions are widely met in natural and artificial systems, which explains the broad applicability of Kepler’s formulation.

Kepler’s Third Law and Exoplanets

One of the most important modern uses of Kepler’s third law is the study of exoplanets, which are planets orbiting stars outside our Solar System. Since these worlds cannot usually be observed directly, astronomers infer their presence and properties through indirect evidence. Kepler’s third law plays a crucial role in this process because it allows the determination of orbital radii, star masses, and planetary periods using limited observational data.

How the Law Supports Exoplanet Detection

When applying Kepler’s third law to exoplanetary systems:

• Astronomers can estimate orbital radius from the measured orbital period of the exoplanet.

• The period can be determined from periodic variations in a star’s brightness (transit method) or from shifts in the star’s spectral lines (radial velocity method).

A schematic illustrating an exoplanet passing in front of its host star and the resulting brightness dip recorded as a light curve. Regular dips indicate the orbital period used in applying Kepler’s third law. The labelled ingress and egress points and limb darkening provide additional detail beyond the OCR specification. Source.

• Knowing the radius enables classification of exoplanets into categories such as hot Jupiters, super-Earths, or temperate-zone planets.

• Multiple planets orbiting the same star can be compared directly, as T²/r³ remains constant for all bodies orbiting that star.

Because the same mathematical form applies independently of star type or planetary composition, the law acts as a foundational tool of modern planetary science.

EQUATION
—-----------------------------------------------------------------
Kepler’s Third Law (T² = (4π²/GM) r³)
T = Orbital period of the orbiting body, measured in seconds
r = Mean orbital radius or semi-major axis, measured in metres
G = Gravitational constant, measured in N m² kg⁻²
M = Mass of central object, measured in kilograms
—-----------------------------------------------------------------

This equation enables quantitative comparison across stellar systems, though in many cases students will apply only the proportional form T² ∝ r³ unless additional data are provided.

Recognising the Broader Physical Insight

Kepler’s third law in its general form reveals a fundamental aspect of gravitational systems: as distance from a central mass increases, the required orbital speed decreases, and the period increases dramatically. This allows the structure of planetary systems to be understood without needing direct measurement of each component. It provides a concise bridge between theoretical physics and observational astronomy, demonstrating how universal laws describe the motion of bodies across vastly different scales.