OCR Specification focus:
‘For mass M, gravitational potential is Vg = −GM/r; consider changes in potential with r.’
Gravitational potential around a point mass describes how the gravitational influence of a single isolated mass changes with distance, shaping energy landscapes in gravitational systems.
Gravitational Potential Around a Point Mass
Understanding the gravitational potential surrounding a point mass is essential for analysing motion, energy, and fields in gravitational systems. The concept of potential provides a more convenient, scalar-based way to describe gravitational effects than directly analysing gravitational force, especially when dealing with radial variations in field strength. At OCR A-Level Physics, gravitational potential is treated relative to infinity, enabling consistent comparisons and energy calculations across different gravitational environments.
The Nature of Gravitational Potential
When discussing gravitational fields, gravitational potential is the key scalar quantity describing how much work per unit mass is required to bring a small test mass from infinity to a particular point in the field. Because gravitational forces are always attractive, the gravitational potential around a point mass is always negative. This negative sign indicates that external work must be done to move a mass from a finite distance back to infinity.
Gravitational Potential: The work done per unit mass in bringing a small test mass from infinity to a specific point in a gravitational field.
This definition establishes gravitational potential as a foundational quantity for gravitational potential energy and for understanding how objects behave within gravitational fields.
A key feature of a point mass is that all gravitational effects act as if the mass is concentrated at a single geometric point. This assumption simplifies gravitational analysis and is fully consistent with the behaviour of spherical masses, which can be modelled as point masses when considered from outside their radius.
Deriving the Potential Around a Point Mass
For a point mass M, the gravitational potential at distance r is expressed as a simple inverse proportionality. This relationship is required by the OCR specification and forms the mathematical basis for interpreting how potential varies with distance.
EQUATION
—-----------------------------------------------------------------
Gravitational Potential (Vg) = −GM / r
Vg = gravitational potential (J kg⁻¹)
G = universal gravitational constant (N m² kg⁻²)
M = mass producing the field (kg)
r = radial distance from the centre of mass (m)
—-----------------------------------------------------------------
The equation reveals several important physical ideas. First, gravitational potential becomes less negative as r increases, approaching zero only at infinity. Secondly, the inverse relationship means that potential decreases in magnitude rapidly near the mass but more slowly at greater distances.
Behaviour of Potential as Distance Changes
The variation of gravitational potential with distance has consequences for energy, orbits, and field strength. Because gravitational potential is defined relative to infinity, any finite value of r corresponds to a negative potential. As the distance increases:
The potential becomes less negative, meaning the gravitational influence weakens.
The gradient of the potential curve decreases, indicating that the rate of change in gravitational influence diminishes with distance.
Escape energy requirements reduce, because smaller amounts of work are needed to move a mass further away at large distances.
These patterns reflect the long-range but weakening nature of gravitational interactions.
Relationship Between Potential and Field Strength
Gravitational potential and gravitational field strength are closely connected. The field strength at any point is the negative gradient of the potential with respect to distance. This relationship means that the shape of the potential function determines the behaviour of the gravitational field itself.
Because the potential follows an inverse relationship, the field strength must follow an inverse-square relationship. This is consistent with Newton’s law of gravitation and ensures that the concepts of energy-based and force-based descriptions of gravitational fields fit together coherently.
After defining the potential, it becomes clear that the gravitational field is strongest at small values of r, where the potential curve is steepest. As r increases, the slope becomes shallower, indicating a weakening field.
For a single isolated point mass M, the gravitational potential at distance r is V = −GM/r, with more negative values at smaller r.
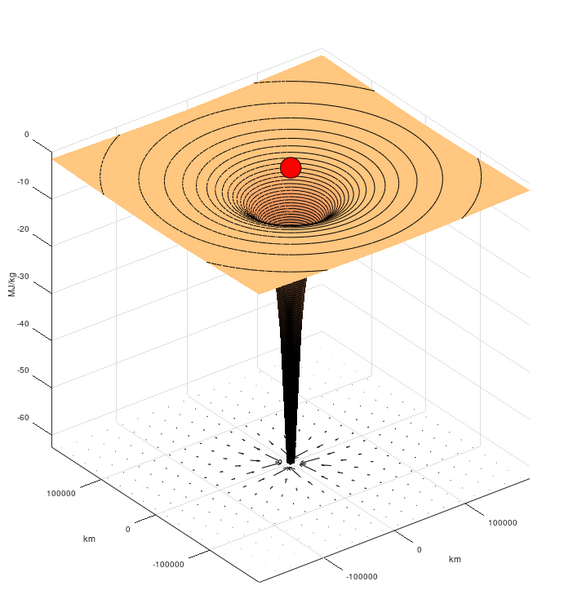
This 3D diagram shows the gravitational potential well around Earth, where deeper regions represent more negative potential. The steep funnel near the centre illustrates the strong gravitational influence close to Earth, while the surface becomes progressively flatter at greater distances. The field-line arrows underneath are additional detail beyond the OCR syllabus requirement. Source.
Key Properties of Gravitational Potential Around a Point Mass
Students should ensure they can recognise and explain the following characteristics, which stem directly from the OCR-required formula:
Always negative
Because gravity is attractive, the potential never becomes positive at finite distance.Zero only at infinity
All gravitational potential values rise toward zero as the distance becomes extremely large.More negative close to the mass
Deep gravitational wells exist around large masses or small values of r.Determines gravitational potential energy
Potential energy for a mass m is obtained by multiplying m by Vg, forming a basis for analysing orbital and escape conditions.Linked directly to field strength behaviour
The shape of the potential curve governs how field strength changes.
In a spherically symmetric field, points at the same radial distance from the mass share the same gravitational potential, forming spherical equipotential surfaces.
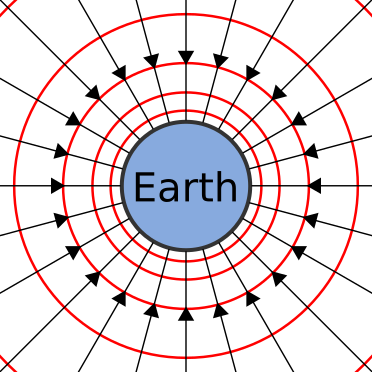
This diagram shows Earth at the centre, with red concentric equipotential surfaces illustrating points of equal gravitational potential. Each ring represents a fixed value of V, confirming that potential depends solely on distance r for a spherical mass. The black field lines provide additional directional information not required for this subsubtopic. Source.
Practical Uses in Physics
Although this subsubtopic focuses specifically on gravitational potential around a point mass, the concept itself underpins many analyses encountered later in gravitational studies. Understanding potential is essential for discussing orbital motions, escape velocity, gravitational potential energy, and the modelling of stellar and planetary systems. The scalar nature of potential makes it especially valuable when multiple gravitational sources are present, as potentials can be combined through simple addition.
Through the OCR-required relationship Vg = −GM/r, students gain a precise and consistent framework for describing the energy landscape created by a point mass, enabling confident application of gravitational principles across a broad range of physical situations.
FAQ
Gravitational potential is the work done per unit mass in bringing a test mass from infinity to a point in the field. It is a property of the gravitational source itself.
Gravitational potential energy depends on the mass placed in the field. It is found by multiplying the gravitational potential by the mass experiencing the field.
A useful way to distinguish them:
• Potential tells you about the landscape of the field.
• Potential energy tells you how an object interacts with that landscape.
Close to the mass, small changes in distance cause large changes in gravitational influence because the field is much stronger.
Further away, gravitational effects weaken significantly, so increasing the distance by the same amount produces only a small change in potential.
This behaviour reflects the structure of the inverse relationship V = -GM/r:
• At small r, dividing by a small number creates large negative values.
• At large r, dividing by a large number produces values close to zero.
In Newtonian gravity, gravitational potential is defined to be zero at infinity and negative everywhere else.
A positive gravitational potential would imply that external work has already been supplied to the system before reaching that point, effectively surpassing the energy required to escape the gravitational field.
Such a situation does not naturally occur around isolated point masses but can appear in modified reference conventions or non-Newtonian gravitational models, which are beyond the OCR course.
Equipotential surfaces represent points of equal gravitational potential, forming concentric spheres around a point mass.
They simplify the understanding of gravitational energy because:
• No work is done when moving along an equipotential surface.
• All changes in potential occur when motion has a component towards or away from the mass.
This is particularly useful in multi-step problems, as it separates path-dependent forces from path-independent energy changes.
Setting gravitational potential to zero at infinity gives a consistent and universal reference point for comparing gravitational effects.
It avoids ambiguity between different gravitational systems and ensures that potential differences have physical meaning.
If another reference point were chosen, calculations of potential energy changes would still work, but:
• Absolute potential values would differ between systems.
• Additional adjustments would be required when combining gravitational influences from different masses.
Using infinity keeps the mathematics simple and standard across Newtonian gravity.
Practice Questions
A point mass M creates a gravitational field. State the expression for the gravitational potential V at a distance r from the mass and explain why the value of V is always negative.
(3 marks)
Question 1 (3 marks)
• Correct expression for gravitational potential: V = -GM/r (1 mark)
• Identification that gravitational potential is negative because gravity is always attractive (1 mark)
• Explanation that work must be done against gravity to move a mass from r to infinity, so potential at any finite distance is less than zero (1 mark)
A spacecraft moves from a distance r1 from a planet of mass M to a larger distance r2, where r2 is much greater than r1. Using the expression for gravitational potential around a point mass, explain how and why the gravitational potential changes during this movement. Include in your answer how this relates to the work done on or by the spacecraft.
(5 marks)
Question 2 (5 marks)
• States that gravitational potential around a point mass becomes less negative as distance increases (1 mark)
• Correct reference to the formula V = -GM/r in explaining this change (1 mark)
• Explains that increasing r reduces the magnitude of V because the gravitational influence weakens with distance (1 mark)
• States that work must be done on the spacecraft to move it to a larger r (1 mark)
• Connects this work to the increase in gravitational potential (i.e., potential energy increases as V becomes less negative) (1 mark)

