OCR Specification focus:
‘For mass m at distance r, gravitational potential energy is Eg = mV = −GMm/r.’
Gravitational potential energy describes how the position of a mass within a gravitational field determines the energy associated with its interactions, enabling predictions of motion, binding, and energy transfer.
Gravitational Potential Energy in Newtonian Gravity
Gravitational potential energy is central to analysing how objects behave in gravitational fields produced by point masses and spherically symmetric bodies. OCR specifies that gravitational potential energy for a mass m at distance r from a mass M is given by the negative inverse-proportional relationship Eg = −GMm/r. This expression ties directly to the concept of gravitational potential and the work done in moving masses within a gravitational field.
Gravitational Potential and Its Role in Energy
The idea of gravitational potential energy arises naturally from the related quantity gravitational potential, which describes the energy per unit mass at a given point. When multiplied by a mass m, this potential becomes the gravitational potential energy associated with that mass.
Gravitational Potential Energy: The energy a mass possesses because of its position in a gravitational field, defined relative to zero potential at infinity.
Because the reference point for gravitational potential is taken at infinity, gravitational potential energy values near a mass are always negative, indicating that external work must be done to move the mass out of the gravitational influence of another body.
A key implication of this definition is that gravitational potential energy reflects how bound a system is. A more negative value corresponds to a more strongly bound mass, while a value approaching zero suggests weaker gravitational binding.
Mathematical Form of Gravitational Potential Energy
The equation for gravitational potential energy must be derived from the gravitational potential created by a mass M. OCR requires students to understand and use the expression:
EQUATION
—-----------------------------------------------------------------
Gravitational Potential Energy (Eg) = −GMm/r
G = Universal gravitational constant (6.67 × 10⁻¹¹ N m² kg⁻²)
M = Mass creating the gravitational field (kg)
m = Test mass experiencing the field (kg)
r = Distance between the centres of the two masses (m)
—-----------------------------------------------------------------
This expression indicates that gravitational potential energy becomes increasingly negative as the separation r decreases, reflecting the greater work required to move the mass to infinity.
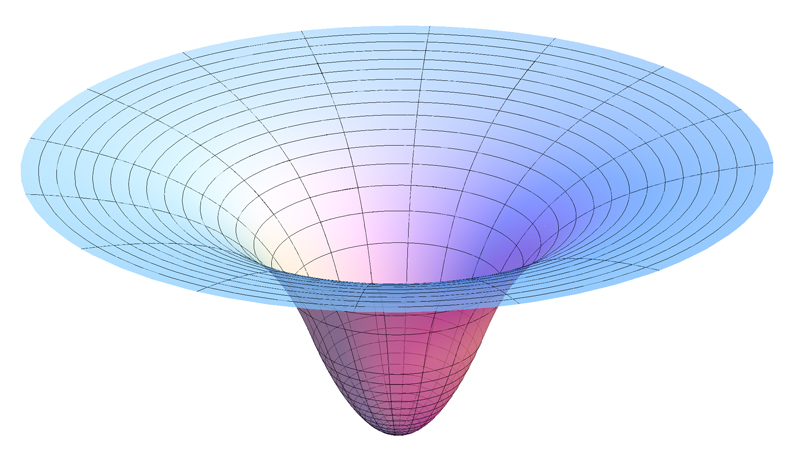
Plot of a gravitational potential well showing how potential becomes more negative closer to a central mass. The depth represents how strongly a mass is gravitationally bound. Although the diagram shows potential per unit mass, its shape corresponds directly to gravitational potential energy behaviour. Source.
The negative sign is significant: in gravitational systems, energy must be supplied to overcome the attractive force. Students should recognise that this mathematical form aligns with earlier knowledge of gravitational potential and that consistent sign conventions are crucial when analysing mechanical energy.
Physical Interpretation of Eg = −GMm/r
Understanding why gravitational potential energy takes this form strengthens conceptual knowledge. When masses interact gravitationally:
Work must be done against gravity to increase their separation.
As distance increases, gravitational potential energy increases (becoming less negative).
At infinite separation, the gravitational interaction becomes negligible, so gravitational potential energy is defined as zero.
These ideas lead to intuitive explanations of orbital mechanics, escape energy considerations, and changes in kinetic energy during gravitational interactions.
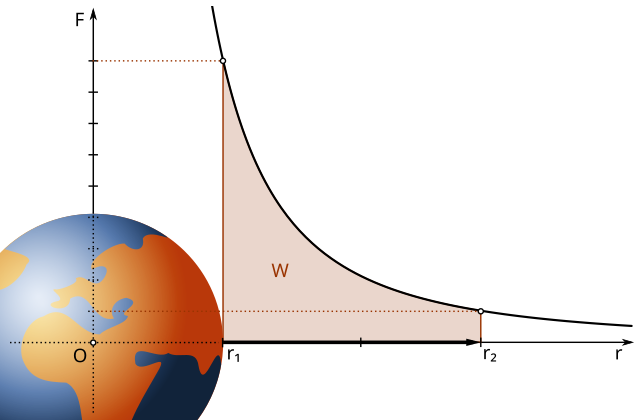
Diagram illustrating a mass being lifted in a gravitational field, showing the direction of gravitational force and displacement. Work done against gravity increases gravitational potential and therefore gravitational potential energy. The layout links spatial displacement to changes in energy. Source.
Features and Behaviour of Gravitational Potential Energy
Several important characteristics emerge from the gravitational potential energy expression, all of which are necessary for OCR A-Level understanding:
Inverse proportionality:
Eg decreases in magnitude as 1/r, meaning gravitational potential energy changes become more pronounced when objects are close together.
Central force nature:
The energy depends only on the radial distance between masses, not on direction or orientation.
Conservative field behaviour:
Gravitational potential energy depends only on initial and final positions, allowing consistent use of energy conservation.
Using Gravitational Potential Energy in Context
Gravitational potential energy is used across many areas of physics to explain and predict the energetic behaviour of massive objects. Its consistent formulation enables analysis of energy transfers in systems such as:
Objects falling towards Earth or other planets
Satellites moving in and out of gravitational wells
Binary star or planetary systems exchanging energy
Escape conditions for spacecraft or atmospheric particles
By linking gravitational potential energy with changes in kinetic energy, students can analyse how orbital motion, gravitational collapse, or projectile paths evolve under Newtonian gravity.
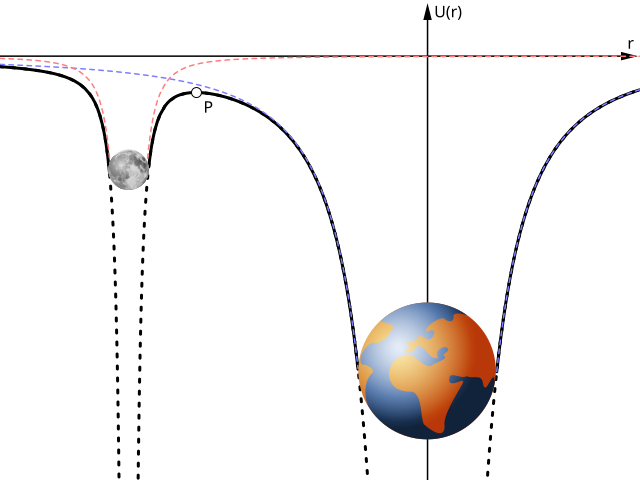
Graph of gravitational potential along the Earth–Moon axis, showing individual and combined potential wells. The combined curve illustrates how potentials from multiple bodies add together. Inclusion of the force-free point extends the concept beyond a single mass but uses the same principles. Source.
Relationship Between Gravitational Potential and Potential Energy
Because gravitational potential energy relies on gravitational potential, the two concepts are tightly connected. When gravitational potential is known:
Multiply the gravitational potential by the mass m to obtain gravitational potential energy
Use this relationship to move between system-wide and per-unit-mass perspectives
Interpret gravitational potential energy changes as the mechanical energy adjustments governing motion
These connections also help students see how gravitational fields store and transfer energy across different situations, reinforcing the unifying principles behind Newton’s law of gravitation.
Key Points for OCR Students
To master this subsubtopic, students should focus on:
Understanding why gravitational potential energy is negative and what this indicates about bound systems
Applying Eg = −GMm/r accurately in gravitational energy problems
Interpreting gravitational potential energy changes as part of broader mechanical energy conservation
Appreciating the conceptual relationship between gravitational potential and gravitational potential energy
Linking gravitational potential energy to real physical processes involving massive bodies
FAQ
Gravitational potential energy indicates how strongly a mass is bound to another object. The more negative the value, the more tightly the mass is gravitationally bound.
Binding energy in this context refers to the energy required to move the mass from its current position to an infinite distance away. It is equal in size to the magnitude of the gravitational potential energy but taken as a positive value.
Setting gravitational potential energy to zero at infinity provides a universal reference point that works for all gravitational systems, regardless of mass or scale.
If another point were chosen as zero, the expression for gravitational potential energy would vary between situations. Using infinity ensures consistency and simplifies comparisons across different gravitational fields.
As the masses approach one another, their gravitational potential energy becomes more negative because the separation distance decreases.
The reduction in gravitational potential energy corresponds to an increase in kinetic energy. This energy transfer drives gravitational collapse in systems such as forming stars or merging binary objects.
Gravitational potential energy varies as 1/r, meaning the rate of change is greatest when r is small.
This produces steep energy gradients near massive bodies. As a result:
Small radial movements close to the surface lead to large energy changes.
Movements far from the mass produce only small changes in potential energy.
Gravitational potential energy itself is not always conserved, but total mechanical energy is conserved unless external forces act.
In astrophysical systems:
Gravitational potential energy may convert into kinetic energy, heat, or radiation.
Energy losses (e.g., tidal heating, atmospheric drag, gravitational waves) mean that total mechanical energy may reduce over time.
However, within an idealised two-body system with no external influences, gravitational potential and kinetic energy exchange while total energy remains constant.
Practice Questions
Question 1 (3 marks)
A spacecraft of mass 850 kg is at a distance r from the centre of a planet of mass M.
(a) State the expression for the gravitational potential energy of the spacecraft in the gravitational field of the planet.
(b) Explain the significance of the negative sign in this expression.
Question 1 (3 marks)
(a) Gravitational potential energy expression: Eg = −GMm/r (1 mark)
(b) Explanation of the negative sign:
Indicates the gravitational field is attractive (1 mark)
Shows that work must be done against gravity to move the object to infinity / gravitational potential energy is zero at infinity and negative closer to the mass (1 mark)
Question 2 (5 marks)
A moon of mass 4.2 × 10^20 kg orbits a planet. At a particular point in its orbit, the moon is 7.8 × 10^7 m from the planet’s centre.
(a) Using the expression for gravitational potential energy, explain how the gravitational potential energy of the moon changes as it moves closer to the planet.
(b) Discuss how gravitational potential energy and kinetic energy interact to maintain a stable orbital motion for the moon.
Question 2 (5 marks)
(a) Explanation of gravitational potential energy changes:
Use of Eg = −GMm/r in qualitative form (1 mark)
As r decreases, the magnitude of Eg increases (becomes more negative) (1 mark)
This indicates the moon becomes more gravitationally bound as it moves closer (1 mark)
(b) Interaction of gravitational potential energy and kinetic energy:
As the moon moves closer, loss of gravitational potential energy leads to gain in kinetic energy (1 mark)
For a stable orbit, total mechanical energy is conserved; changes in potential and kinetic energy balance to maintain orbital motion (1 mark)

