OCR Specification focus:
‘Define escape velocity and predict atmospheric loss of atoms from planetary bodies.’
Escape velocity describes the minimum speed an object must reach to move away from a gravitational field without further propulsion, linking gravitational energy, planetary atmospheres, and space exploration.
Escape Velocity: Core Concept
Escape velocity is a crucial idea in gravitational physics because it connects the gravitational potential energy of a body to the minimum kinetic energy required for an object to leave that body's gravitational influence. In simple terms, it is the speed needed to reach effectively infinite separation from a planet or moon without turning back. The OCR specification emphasises not only understanding this velocity but also using it to predict atmospheric loss, a key concept in planetary science.
The Need for a Minimum Speed
When a mass moves against a gravitational field, it must expend energy to overcome the attractive force of the planet or moon. Escape velocity provides a threshold value: if the object's initial kinetic energy equals or exceeds the energy required to overcome gravitational attraction, then the object can leave the gravitational field entirely. This value depends on the mass and radius of the celestial body.
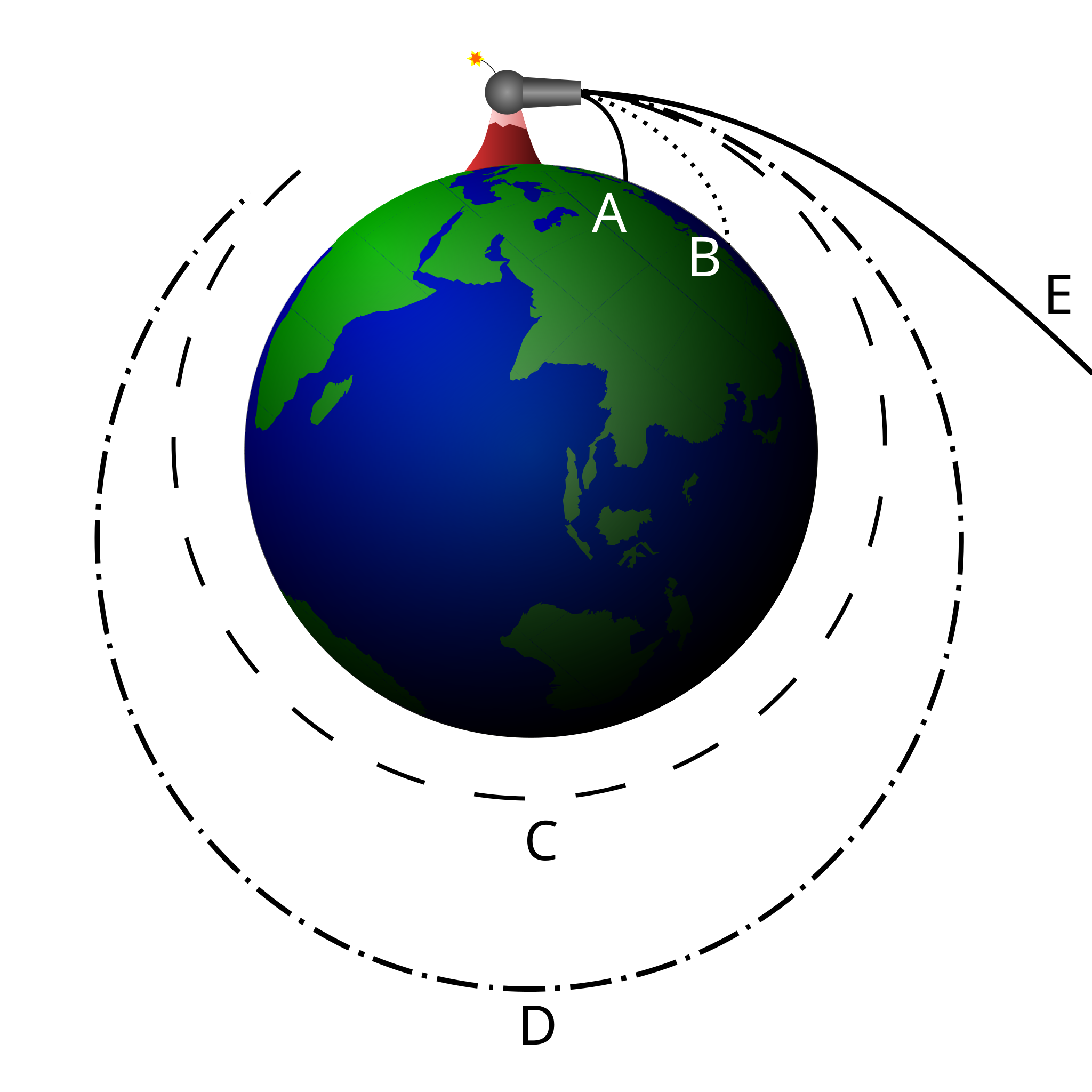
Illustration of Newton’s cannon: a projectile fired from a high mountain at increasing speeds follows trajectories that are suborbital, orbital, or escaping. The highest-speed path shows escape from Earth’s gravity, embodying the concept of escape velocity as the threshold between bound and unbound motion. The multiple labelled paths for different orbits go beyond the OCR requirement but simply elaborate how speeds below escape velocity produce curved, bound trajectories. Source.
Definition of Escape Velocity
Students encounter the term early in gravitational studies, making a precise definition essential.
Escape velocity: The minimum speed an object must have at a planet’s surface (or given distance r) to move to infinity without further propulsion.
In practice, escape velocity is derived by equating the kinetic energy of a body to the gravitational potential energy required to lift it from its starting position to infinity. The underlying reasoning is rooted in conservation of energy.
A normal explanatory sentence must separate definition and equation blocks, ensuring clarity in presentation and cognitive flow for learners.
EQUATION
—-----------------------------------------------------------------
Escape Velocity (vₑ) = √(2GM / r)
vₑ = Escape velocity in metres per second (m s⁻¹)
G = Universal gravitational constant in newton metre² per kilogram² (N m² kg⁻²)
M = Mass of the planet or body in kilograms (kg)
r = Distance from the planet’s centre to the point of launch in metres (m)
—-----------------------------------------------------------------
The equation demonstrates that escape velocity depends only on the gravitational properties of the body being escaped from and the distance from its centre, not on the mass of the escaping object.
Physical Interpretation and Key Features
Understanding the Energy Requirement
To escape the gravitational influence of a planet, an object must have total mechanical energy equal to or greater than zero.
If total mechanical energy is negative, the object is gravitationally bound.
If it reaches zero, the object has just enough energy to reach infinity with no spare kinetic energy.
If positive, the object escapes with kinetic energy remaining.
This explains why escape velocity represents the boundary between bound and unbound motion in gravitational systems.
Common Misconceptions
Students must understand that:
Escape velocity is a speed, not a requirement for continuous thrust.
Rockets do not need to reach escape velocity instantly; they can accelerate gradually because they provide continuous propulsion.
Escape velocity varies with altitude because gravitational potential changes with distance r from the planet’s centre.
Atmospheric Loss and Escape Velocity
Linking Escape Velocity to Planetary Atmospheres
The specification requires students to predict atmospheric loss of atoms using escape velocity. The connection arises from thermal motion in gases. In planetary atmospheres, gas particles move at a range of speeds determined by temperature. At high temperatures, some particles in the distribution may reach or exceed escape velocity.
Mechanism of Atmospheric Escape
Atmospheric loss occurs when individual atoms or molecules achieve speeds high enough to escape the planet’s gravitational field. This is strongly influenced by:
Planetary mass (affects escape velocity)
Planetary radius (determines gravitational potential at the surface)
Atmospheric temperature (higher temperature increases particle speeds)
Particle mass (lighter particles move faster at a given temperature)
Why Some Planets Lose Atmospheres More Easily
Because escape velocity depends on √(M/r), planets with small mass or large radius have relatively low escape velocities. This makes atmospheric retention more difficult.
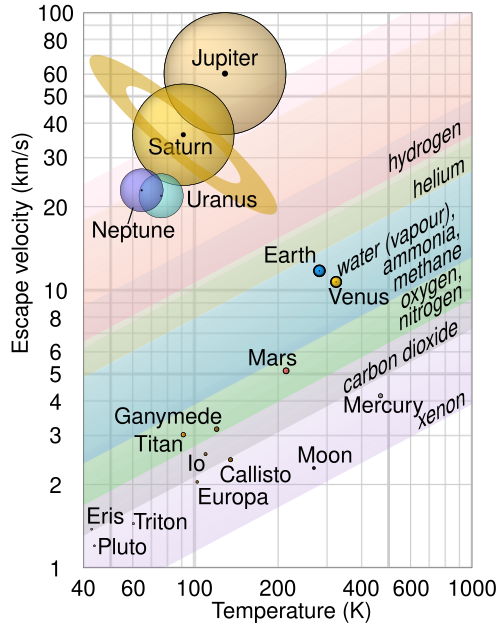
Graph of Solar System bodies on a speed–temperature plot, with dashed lines showing the threshold at which hydrogen and oxygen molecules can escape. Objects lying above a gas’s line cannot retain that gas over long timescales, while those below can keep it gravitationally bound, illustrating how escape velocity and surface temperature control atmospheric loss. The detailed numerical values and multiple planetary labels go beyond the OCR specification but serve only to quantify the same relationship between escape velocity, temperature, and atmospheric escape discussed in the notes. Source.
This makes atmospheric retention more difficult. For example:
Low-mass bodies such as the Moon and Mercury cannot retain light gases over geological timescales.
Massive planets like Jupiter can retain even hydrogen and helium due to extremely high escape velocities.
Thermal Speeds and Atmospheric Retention
To understand atmospheric loss quantitatively, students compare typical thermal speeds of particles with escape velocity:
If the thermal speed of a gas is a significant fraction of the escape velocity, that gas is likely to escape over time.
Light particles (hydrogen, helium) are the most likely to exceed escape velocity because they move faster for the same temperature.
Consequences for Planetary Environments
Atmospheric loss has broad implications in planetary science, astrophysics, and climate theory. It helps explain:
Why Earth retains a substantial atmosphere while Mars has lost most of its original gases.
How exoplanet atmospheres evolve over billions of years.
Why gas giants accumulate vast atmospheres dominated by light elements.
Summary of Key Learning Priorities
Escape velocity links gravitational fields, potential energy, and planetary motion.
Calculating escape velocity allows prediction of whether atoms or molecules can leave a planet’s atmosphere.
The relationship between thermal speeds and escape velocity is central to understanding atmospheric evolution across planetary bodies.
FAQ
Escape velocity decreases with increasing altitude because the distance from the planet’s centre increases, reducing the gravitational potential energy that must be overcome.
At very large distances, escape velocity approaches zero, since gravitational influence decreases with the inverse-square law.
A perfectly spherical planet produces a symmetrical gravitational field, meaning gravitational potential depends only on distance from the centre, not direction.
This symmetry ensures escape velocity is identical in every direction, provided the planet does not rotate or possess significant mass irregularities.
Rotation reduces the effective escape velocity at the equator because the planet’s surface is already moving relative to its axis.
• At the equator, part of the required velocity is provided by rotational speed.
• At the poles, rotation contributes no tangential speed, so escape velocity is slightly higher.
• The effect is small but measurable for planets with rapid rotation.
Yes. Escape velocity is only required for objects that stop accelerating immediately after launch.
With continuous propulsion, a spacecraft can gradually accumulate the necessary energy to escape, even at speeds below the classical escape velocity at any instant.
The key requirement is that its total energy eventually becomes zero or positive relative to the planet.
Atmospheric retention is influenced by more than escape velocity alone.
• Lower atmospheric temperatures reduce molecular speeds.
• Chemical reactions can lock gases into surface materials.
• Magnetic fields can shield atmospheres from solar wind stripping.
• High atmospheric pressure reduces upward diffusion of light gases.
These combined effects can allow a planet with modest escape velocity to maintain a substantial atmosphere.
Practice Questions
Question 1 (2 marks)
State what is meant by escape velocity and explain why it does not depend on the mass of the escaping object.
Question 1 (2 marks)
• Escape velocity is the minimum speed required for an object to escape a planet’s gravitational field without further propulsion. (1)
• It does not depend on the object's mass because both gravitational potential energy and kinetic energy contain the object's mass, which cancels when equated. (1)
Question 2 (5 marks)
A planet has a mass of 4.8 × 10^24 kg and a radius of 3.4 × 10^6 m.
(a) Explain the physical meaning of escape velocity in terms of energy.
(b) Show how escape velocity can be derived using the principle of conservation of energy.
(c) Comment on why lighter atmospheric gases are more likely to escape from this planet than heavier gases.
Question 2 (5 marks)
(a)
• Escape velocity corresponds to the point where the total mechanical energy of an object becomes zero. (1)
• At this speed the object has just enough kinetic energy to reach infinite distance with no energy remaining. (1)
(b)
• Use conservation of energy: kinetic energy at the surface equals the gravitational potential energy needed to reach infinity. (1)
• 1/2 mv^2 = GMm / r leading to v = sqrt(2GM / r). (1)
(c)
• Lighter gas molecules have higher average speeds at a given temperature. (1)
• They are therefore more likely to reach or exceed escape velocity and leave the atmosphere. (1)

