The Doppler effect for electromagnetic waves underpins how astronomers measure motion in the Universe, revealing whether distant objects are approaching or receding and enabling velocity determination.

The Doppler Effect for Light

The Doppler effect is the change in observed frequency or wavelength of a wave caused by relative motion between the source and the observer. Although originally described for sound, the principle applies equally to electromagnetic radiation, including light from stars and galaxies. For OCR A-Level Physics, the focus is specifically on using Doppler shift relations to quantify motion from observed spectral features.

When a source of light moves towards an observer, its waves arrive more frequently, producing a higher observed frequency and a shorter wavelength, known as a blueshift. When the source moves away, the observed frequency decreases and the wavelength becomes longer, producing a redshift.

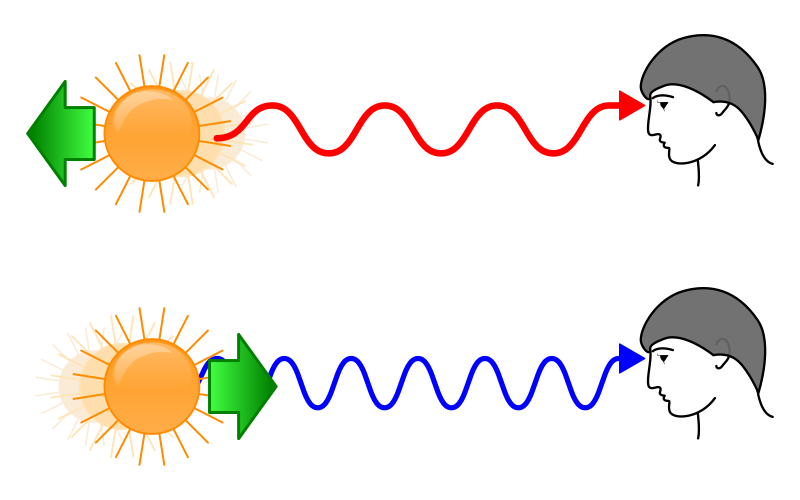
Redshift and blueshift for light emitted by a moving star. The upper panel shows recession with light stretched to longer wavelengths, while the lower panel shows approach with compressed, shorter wavelengths. Source.

These shifts provide essential diagnostic tools in astrophysics.

Students must be comfortable with the link between measured wavelength/frequency changes and the line-of-sight velocity of astronomical objects, which follows directly from the Doppler effect.

Defining Key Terminology

Before exploring the physics further, it is important to clarify essential terminology relevant to Doppler shift analysis.

A redshift does not imply the object is literally red; rather, its spectral lines shift towards the red end of the spectrum.

Following on from redshift, an analogous concept describes motion in the opposite direction.

These shifts form the basis for interpreting stellar and galactic motion using spectroscopy, the primary observational tool for Doppler measurements in astronomy.

Spectral Lines and Motion

Spectral lines provide precise reference markers that make Doppler measurements possible. Atoms produce unique absorption or emission lines corresponding to electron transitions. When an astronomical object moves, the entire pattern of spectral lines shifts uniformly.

This shift is measured by comparing the rest wavelength of a known spectral line (its value when the source is stationary relative to Earth) with the observed wavelength. A displacement towards longer wavelengths indicates recession; a shift towards shorter wavelengths indicates approach.

Key points in interpreting Doppler-shifted spectra include:

• Uniform line displacement, showing that the shift is not due to changes in atomic structure but relative motion.

• Magnitude of shift being proportional to the object’s radial velocity.

• Use of narrow, well-defined spectral lines, which increases measurement precision.

• Applicability at all scales, from exoplanets tugging on their host stars to galaxies receding across cosmological distances.

Quantifying Doppler Shift

To determine the velocity of a moving light source, the Doppler relation for electromagnetic waves is required. For non-relativistic speeds (significantly less than the speed of light), the change in frequency or wavelength is directly proportional to velocity.

EQUATION
—-----------------------------------------------------------------
Doppler Shift (Wavelength) = Δλ / λ = v / c
Δλ = Change in observed wavelength (m)
λ = Rest wavelength of the spectral line (m)
v = Radial velocity of source relative to observer (m s⁻¹)
c = Speed of light in vacuum (m s⁻¹)
—-----------------------------------------------------------------

This expression allows astronomers to express motion quantitatively using observational data alone. After using the equation, it remains important to interpret the sign of the velocity: positive values represent recession, whereas negative values represent approach.

Students should note that this formula applies when velocities are small compared with the speed of light. At high velocities, a full relativistic treatment is needed, but this lies beyond the OCR specification requirement.

Practical Interpretation of Doppler Shifts

Understanding the Doppler effect means linking spectral measurement to motion. In astronomy, this is especially valuable because direct spatial displacements are typically unobservable over human timescales.

Important applications include:

• Measuring stellar radial velocities to infer orbital motion or identify binary star systems.

• Detecting exoplanets using periodic Doppler oscillations of the host star’s spectral lines.

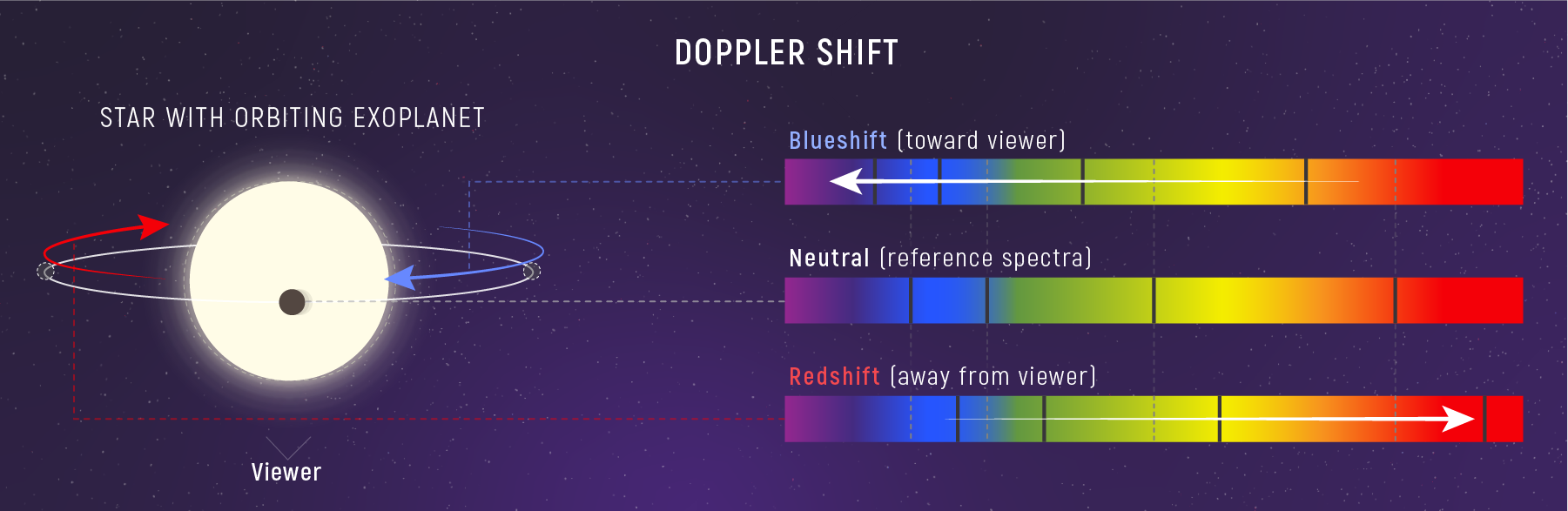
Doppler shift of a star’s spectrum caused by an orbiting exoplanet. The spectra show how absorption lines move as the star alternately approaches and recedes. The inclusion of the planet extends beyond the OCR requirement but illustrates the same velocity–spectral shift principle. Source.

• Determining galaxy motion, a fundamental step in cosmological analysis.

• Monitoring stellar oscillations, providing insights into internal stellar structure.

These processes rely on highly precise spectroscopic data, often from diffraction gratings or high-resolution instruments capable of resolving tiny wavelength shifts.

Electromagnetic Versus Sound Doppler Effect

The Doppler effect for light differs from that for sound because electromagnetic waves do not require a medium. As a result:

• There is no dependence on a background medium’s motion.

• The shift arises purely from relative motion, not interactions with any intervening substance.

• At high speeds, relativistic corrections become necessary due to the constant speed of light for all observers.

Despite these differences, the conceptual basis remains similar: waves from a moving source reach the observer at altered intervals.

Observational Considerations in Astronomy

Accurate Doppler measurements depend on careful instrument calibration and knowledge of laboratory rest wavelengths. To interpret Doppler shifts effectively, students should consider:

• Instrumental effects, which must be corrected to avoid false velocity readings.

• Earth’s orbital motion, which introduces its own Doppler shift and must be removed through data processing.

• Interstellar medium effects, which may broaden spectral lines but do not shift their central wavelength.

• Choice of spectral lines, as some transitions provide clearer, sharper features.

These considerations ensure that Doppler-derived velocities reflect true astrophysical motion rather than observational artefacts.

Broader Relevance in Astrophysics

Doppler measurements underpin key discoveries in modern astrophysics, including orbital dynamics, stellar rotation, and galaxy recession. They form an essential tool for exploring the structure and evolution of cosmic systems and remain a core skill for advanced physics students studying the motions of astronomical objects.