OCR Specification focus:
‘For receding galaxies v ≈ H₀d; H₀ units include s⁻¹; estimate age as t ≈ H₀⁻¹.’
Hubble’s law provides one of the most direct and powerful pieces of evidence for the expanding Universe, linking a galaxy’s recessional speed with its distance and enabling age estimation.
Hubble’s Law
Hubble’s law is a foundational relationship in observational cosmology linking the recessional motion of distant galaxies with their separation from the observer. It is interpreted as evidence that space itself is expanding uniformly on large scales. This expansion is not due to galaxies moving through space but rather to the stretching of space-time, causing the wavelengths of emitted light to become redshifted. The law therefore provides essential context for understanding the size, scale, and long-term evolution of the Universe.
Hubble’s Law: The empirical relationship stating that a galaxy’s recessional velocity is proportional to its distance from the observer.
This relationship is central to the specification because it provides a practical method for estimating the age of the Universe through the reciprocal of the Hubble constant.
The Recessional Velocity of Galaxies
For astronomical observations, determining how a galaxy moves relative to Earth is crucial. Light from distant galaxies is usually shifted towards longer, redder wavelengths, signalling that the object is moving away. The greater the redshift, the faster the recession. Hubble’s analysis of many galaxies revealed a consistent trend: more distant galaxies show larger redshifts, implying higher recessional velocities.
EQUATION
—-----------------------------------------------------------------
Hubble’s Law (v = H₀d) = v = H₀ d
v = Recessional velocity of the galaxy in m s⁻¹
H₀ = Hubble constant in s⁻¹ (may also appear in km s⁻¹ Mpc⁻¹)
d = Distance from Earth to the galaxy in metres or megaparsecs
—-----------------------------------------------------------------
The proportionality expressed in the equation allows astronomers to infer distances from recessional velocities and vice versa, provided the value of H₀ is known.
On a graph of recessional velocity against distance, the gradient of the best-fit straight line is equal to the Hubble constant H₀.
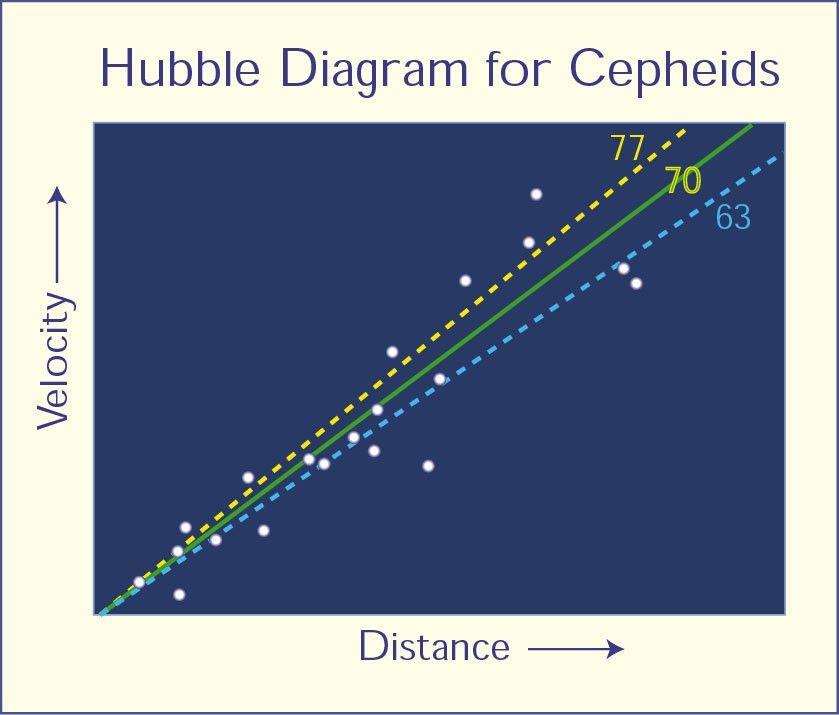
A Hubble diagram showing the linear relationship between distance and recessional velocity. The solid line represents Hubble’s law, while dashed alternatives illustrate different possible values of the Hubble constant, providing more numerical detail than required but reinforcing how H₀ is determined. Source.
Units and Interpretation of the Hubble Constant
The specification emphasises that the Hubble constant can be expressed in s⁻¹, a unit that clarifies its physical meaning. When written in the more common form of km s⁻¹ Mpc⁻¹, the constant describes how much recessional velocity increases per megaparsec of distance. Converting this into s⁻¹, a direct inverse time dimension emerges. This is especially useful when relating the constant to the age of the Universe.
Physical Significance of H₀
The value of the Hubble constant encapsulates the current rate of cosmic expansion. A larger H₀ implies that galaxies recede faster at a given distance, while a smaller value suggests slower expansion. Although the expansion rate has changed throughout cosmic history, H₀ describes the present-day expansion and is essential for many cosmological models.
Estimating the Age of the Universe
One of the most powerful conceptual outcomes of Hubble’s law is the ability to estimate how long the Universe has been expanding. By assuming that galaxies have been moving apart at roughly the current rate since the beginning of the Universe, an approximate age can be inferred.
Age Estimate (t ≈ H₀⁻¹): An approximation for the age of the Universe based on the reciprocal of the Hubble constant.
This follows logically from the proportional relationship in Hubble’s law. If distance increases linearly with velocity, then the reciprocal of the expansion rate gives an estimate of how long the expansion has been occurring.
A sentence must occur here to separate definition or equation sections before another block appears.
EQUATION
—-----------------------------------------------------------------
Age of Universe (t ≈ 1/H₀) = t ≈ 1 / H₀
t = Estimated age of the Universe in seconds
H₀ = Hubble constant in s⁻¹
—-----------------------------------------------------------------
Assuming the expansion rate has remained roughly constant, the age of the Universe can be estimated using t ≈ 1/H₀.
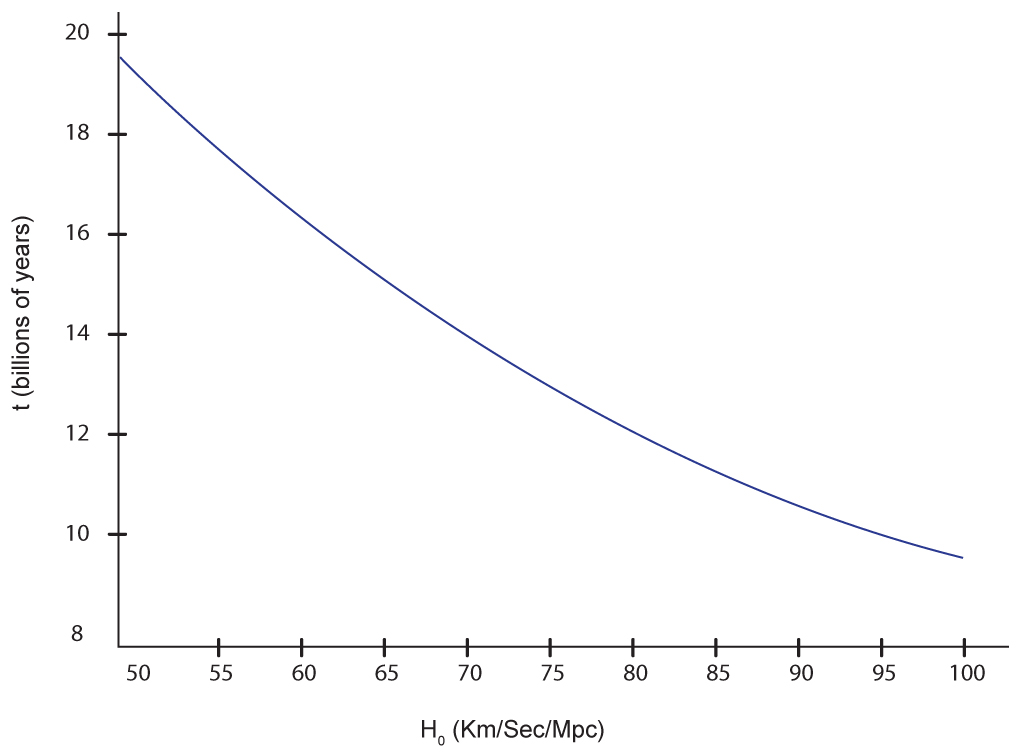
A graph illustrating the inverse relationship between the Hubble constant and the estimated age of the Universe. Higher values of H₀ correspond to a younger Universe, while lower values indicate an older one. The plot includes detailed numerical scales beyond the OCR requirement but clearly demonstrates the core concept. Source.
Observational Foundations
Hubble’s law was established through systematic measurement of galaxy distances and redshifts. These observations revealed a uniform expansion consistent across the sky, reinforcing the cosmological principle that the Universe is homogeneous and isotropic on large scales.
Key observational elements include:
Redshift measurements, providing recessional velocities via Doppler interpretation.
Standard candles, such as Cepheid variables, enabling reliable distance estimates.
Large galaxy surveys, confirming the linear relationship across vast scales.
These observations form the backbone of modern cosmology, validating the expanding-Universe model and supporting the Big Bang framework.
Summary of Key Points for OCR Study (without concluding the notes)
Hubble’s law: recessional velocity proportional to distance.
H₀ expressed in s⁻¹ gives clear physical meaning.
t ≈ H₀⁻¹ provides an approximate cosmic age.
Observational evidence supports uniform expansion of the Universe.
FAQ
Recessional velocity is determined by measuring the redshift of the galaxy’s spectral lines. These lines shift towards longer wavelengths when the galaxy is moving away.
The amount of shift is compared to laboratory wavelengths of the same elements. From this, the change in wavelength can be converted into a velocity using the Doppler relation for electromagnetic waves.
Modern telescopes collect high-resolution spectra, allowing extremely precise measurements even for faint galaxies billions of light-years away.
Galaxies have additional motions known as peculiar velocities, caused by local gravitational interactions within clusters or groups.
These motions can add to or subtract from the recessional velocity predicted by Hubble’s law.
• Nearby galaxies often show the largest deviations because their gravitational interactions dominate over cosmic expansion.
• Very distant galaxies match the linear relationship more closely because their expansion-driven velocities are much larger than their peculiar velocities.
No. Hubble’s law describes large-scale expansion of space and does not apply within gravitationally bound systems.
Stars within the Milky Way orbit under the influence of gravity, and any effects of cosmic expansion are negligible compared with these gravitational forces.
Even neighbouring galaxies within the Local Group, such as Andromeda, do not follow Hubble’s law because the group is gravitationally bound.
Using km s⁻¹ Mpc⁻¹ gives astronomers an intuitive sense of how quickly recessional velocity increases with distance on cosmic scales.
It directly relates observable quantities:
• km s⁻¹ matches the units used to express Doppler-measured recessional velocity
• Mpc is a convenient large-scale distance unit for galaxies
Converting to s⁻¹ is straightforward and reveals the physical meaning of H0 as an inverse time, but the mixed units are more practical for observational work.
Uncertainty arises from both measurement limitations and physical assumptions.
Key sources include:
• variation in published values of H0 due to different observational methods
• calibration errors in standard candles used to estimate distances
• the assumption of constant expansion rate, which is not strictly true
• the influence of dark energy and early deceleration, which alter the expansion history
These factors lead to a range of possible ages rather than a single precise value.
Practice Questions
Question 1 (2 marks)
A distant galaxy is observed to have a recessional velocity of 1.8 × 10⁶ m s⁻¹.
Its distance from Earth is measured to be 2.5 × 10²² m.
Explain how this observation provides evidence for Hubble’s law.
Question 1 (2 marks)
• States that recessional velocity is proportional to distance / more distant galaxies recede faster. (1)
• Shows that the given galaxy fits this trend because the large distance corresponds to a large recessional velocity. (1)
Question 2 (5 marks)
Astronomers use Hubble’s law to estimate the age of the Universe.
Explain how the relationship between recessional velocity and distance leads to an estimate of the age.
In your answer, refer to:
• the form of Hubble’s law
• the meaning of the Hubble constant
• why the reciprocal of the Hubble constant gives an approximate age of the Universe
• one limitation of this estimation method.
Question 2 (5 marks)
• States Hubble’s law: recessional velocity is proportional to distance / v = H0 d. (1)
• Identifies H0 as the Hubble constant that gives the rate of expansion of the Universe. (1)
• Explains that if velocity increases linearly with distance, then 1/H0 gives a characteristic timescale for expansion. (1)
• States that 1/H0 provides an estimate of the age of the Universe. (1)
• Gives one limitation, e.g.: assumes constant expansion rate over time / ignores changes due to dark energy or deceleration in early Universe / observational uncertainties in H0. (1)

