OCR Specification focus:
‘Define capacitance C with Q = CV; state farad as the unit of capacitance.’
Capacitance underpins how electrical systems store charge and respond to potential differences, making it essential for understanding circuits, energy storage, and the behaviour of components.
Understanding Capacitance
Capacitance is a foundational concept in circuit theory, governing how much electric charge can be stored on a pair of conducting plates for a given potential difference. When a capacitor is placed across a power supply, charge builds up on its plates until the potential difference across it matches the supply. At this point, the capacitor is said to be fully charged. The ability of the device to store charge for each volt applied is what defines its capacitance.
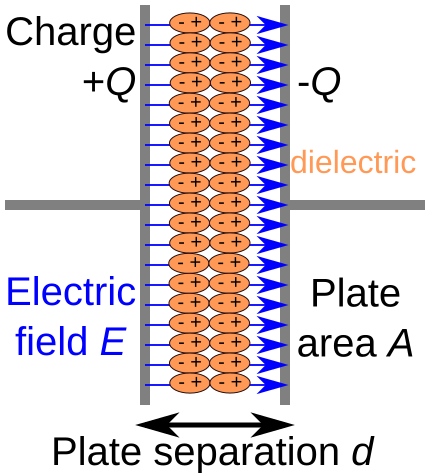
A parallel-plate capacitor diagram showing plates, dielectric, charge distribution, and electric field. Extra geometric detail shown is not required by the syllabus, but it helps illustrate why capacitance varies between capacitors. Source.
Capacitance: The ability of a component to store charge per unit potential difference across its plates.
In practice, capacitance determines how components behave in both static and dynamic circuit conditions. A higher capacitance indicates that more charge can be held for the same applied potential difference. Conversely, a low capacitance implies limited charge storage capability. This relationship is at the heart of many timing, filtering, and energy-storage applications in electronics.
The Relationship Between Charge, Capacitance, and Potential Difference
The OCR specification highlights the essential equation Q = CV, which mathematically links charge (Q), capacitance (C), and potential difference (V). This relationship is linear for an ideal capacitor within operating limits, meaning that doubling the potential difference doubles the charge stored. Even though real capacitors show minor deviations due to leakage currents or breakdown, the linear model is accurate for A-Level study.
EQUATION
—-----------------------------------------------------------------
Capacitance Relationship (Q = CV) = Q = C V
Q = Charge stored on one plate of the capacitor, measured in coulombs (C)
C = Capacitance of the capacitor, measured in farads (F)
V = Potential difference across the capacitor, measured in volts (V)
—-----------------------------------------------------------------
It is important to understand that charge does not flow through a capacitor in the same way it does through a resistor. Instead, electrons accumulate on one plate while being removed from the other. The result is an electric field between the plates, storing energy in the process. The equation Q = CV describes the equilibrium quantities once the capacitor is fully charged under steady conditions.
The Farad: Unit of Capacitance
Capacitance is measured in farads (F), the SI unit named after Michael Faraday. One farad is a very large unit in practical circuit design — most everyday capacitors range from microfarads (µF) down to picofarads (pF). Devices storing whole farads are typically supercapacitors used for specialised applications such as backup power and memory protection.

A real electrolytic capacitor labelled 4700 μF, 35 V, with the definition of the farad shown above. The unrolled internal structure is additional detail but helps relate the unit of capacitance to a physical component. Source.
Farad: The unit of capacitance equal to one coulomb per volt.
Although large-valued capacitors exist, they rely on advanced materials and structures to increase the surface area between plates or to decrease the separation, thereby increasing capacitance. In the context of A-Level Physics, understanding the magnitude of the farad helps place typical component values into perspective and reinforces why prefixes such as micro- and nano- are commonly used.
A capacitor’s physical structure determines its capacitance. The larger the plate area and the smaller the separation, the greater the capacitance. Dielectric materials placed between the plates also influence capacitance by reducing the effective electric field and allowing more charge to be stored for the same potential difference.
Physical Interpretation of Q = CV
The equation Q = CV is more than a mathematical rule; it offers a physical explanation of capacitor behaviour:
Q is proportional to V, meaning potential difference directly influences how much charge accumulates.
C acts as the proportionality constant, representing the ability of the capacitor to store charge.
The capacitor resists changes in voltage, because charge must either accumulate or leave its plates to alter the potential difference across them.
This relationship is central to understanding how capacitors interact with other components in circuits. For instance, when connected in series or parallel (covered in separate subsubtopics), their combined capacitance changes the total charge-storage characteristics of the system. However, the core Q = CV relationship remains valid for each individual component.
Behaviour During Charging
Although this subsubtopic focuses on capacitance itself, recognising the immediate implications of Q = CV helps build an intuitive picture of capacitor behaviour. When a potential difference is applied:
Electrons flow from one plate to the other via the external circuit.
One plate gains electrons and becomes negatively charged.
The opposite plate loses electrons and becomes positively charged.
The resulting charge separation creates an electric field and a corresponding potential difference.
Charging continues until the potential difference across the capacitor equals the supply voltage. At this point, current ceases and Q = CV gives the final stored charge.
Importance in Circuit Analysis
Understanding Q = CV enables students to interpret capacitor properties correctly and anticipate how they behave under various conditions. Capacitance affects:
How much energy the capacitor can store.
How quickly voltage changes across the capacitor in transient situations.
How capacitors influence the distribution of potential differences in complex circuits.
Why capacitors appear to block direct current while allowing alternating signals to pass depending on frequency.
By mastering the definition of capacitance, the farad, and the Q = CV relationship, students build a solid framework for all subsequent capacitor topics in the OCR A-Level Physics course.
FAQ
Capacitance depends on how easily charge can be stored on the plates, which is determined by geometry and materials.
A capacitor will have a larger capacitance if:
• the plate area is increased
• the separation between plates is reduced
• a dielectric with a higher permittivity is used
These physical factors affect the proportionality constant C, even though Q = CV still governs how charge and potential difference relate.
Dielectrics increase a capacitor’s ability to store charge by reducing the electric field that forms between the plates.
This allows more charge to accumulate for the same applied voltage.
They also prevent electrical breakdown, enabling capacitors to operate safely at higher potential differences without sparking across the gap.
One farad represents storing one coulomb per volt, which is a very large amount of charge for most circuits.
As a result, typical electronic components use:
• microfarads (10⁻⁶ F)
• nanofarads (10⁻⁹ F)
• picofarads (10⁻¹² F)
High-capacitance components such as supercapacitors exist, but they are physically large and used mainly for specialised energy-storage tasks.
Real capacitors can deviate slightly from ideal behaviour.
For example:
• leakage currents cause charge to slowly escape
• imperfections in the dielectric reduce the proportional accuracy
• high voltages can lead to dielectric breakdown, destroying the constant relationship
Under normal operating conditions, however, deviations are small enough that Q = CV remains a valid model for A-Level Physics.
When charging, electrons accumulate until the electric field between the plates produces a potential difference equal to the supply.
Once this equilibrium is reached, there is no net force pushing additional charge onto the plates.
At this point the capacitor is fully charged, current drops to zero, and no further charge can accumulate unless the applied voltage changes.
Practice Questions
Question 1 (2 marks)
A capacitor has a capacitance of 220 microfarads. Explain what is meant by the term capacitance.
Question 1 (2 marks)
• Capacitance is the charge stored per unit potential difference across a capacitor. (1 mark)
• It is a measure of how much charge a capacitor can store for each volt applied. (1 mark)
Question 2 (5 marks)
A student investigates how the charge stored on a capacitor varies with the potential difference across it.
(a) State the equation that relates charge, capacitance, and potential difference.
(b) Describe how the student could determine the capacitance of the capacitor using measurements from the investigation.
(c) Explain why doubling the potential difference across the capacitor results in a doubling of the charge stored.
Question 2 (5 marks)
(a) Q = C V. (1 mark)
(b)
• Measure the charge stored for different values of potential difference. (1 mark)
• Plot a graph of charge (vertical axis) against potential difference (horizontal axis). (1 mark)
• Determine the gradient of the straight-line graph; the gradient equals the capacitance. (1 mark)
(c)
• Charge is directly proportional to potential difference for an ideal capacitor. (1 mark)
• Capacitance is constant, so increasing the potential difference increases the stored charge by the same factor. (1 mark)

