OCR Specification focus:
‘Explain charging and discharging a capacitor through a resistor and predict current, voltage, and charge changes.’
Charging and discharging a capacitor through a resistor is a fundamental transient process in electric circuits, revealing how charge, voltage, and current evolve over time in predictable ways.
Charging and Discharging Through a Resistor
When a capacitor first appears in a circuit connected with a resistor, its behaviour changes dynamically as charge accumulates or is released. The transient response is governed by the interaction between the capacitor’s ability to store charge and the resistor’s opposition to current flow.
Capacitor: A device that stores electrical charge on two separated plates, creating a potential difference when charged.
A capacitor charges when connected to a power supply through a resistor, and discharges when the supply is removed and the capacitor is connected across a resistor.

This diagram shows a basic series RC circuit in which a resistor controls the current flowing to and from a capacitor. It supports discussion of how the capacitor charges or discharges depending on the configuration. The layout contains no additional components, keeping the focus on the key behaviour relevant to this subsubtopic. Source.
This process involves changes in charge (Q), potential difference (V), and current (I). Each quantity evolves over time in a characteristic, non-linear way described by exponential functions.
The Nature of Charging
During charging, electrons are driven from one plate to the other by the external supply. This movement gradually builds an electric field across the plates.
Charging (capacitor): The process in which electrons flow onto or off the capacitor plates, increasing the stored charge and raising the potential difference across the plates.
At the moment charging begins, the current is at its maximum because the potential difference across the capacitor is initially zero. As charge accumulates:
The capacitor’s potential difference increases.
The current decreases, because the growing capacitor voltage opposes the supply.
EQUATION
—-----------------------------------------------------------------
Capacitor Charging (Voltage) = V(t) = V₀(1 − e^(−t/RC))
V(t) = Potential difference across capacitor at time t (volts, V)
V₀ = Supply potential difference (volts, V)
t = Time since charging began (seconds, s)
R = Resistance (ohms, Ω)
C = Capacitance (farads, F)
—-----------------------------------------------------------------
This charging behaviour continues until the capacitor reaches the supply voltage, at which point the current becomes negligible. The resistor ensures that the charge transfer is gradual rather than instantaneous.
The Nature of Discharging
Discharging occurs when the charged capacitor is connected across a resistor without a power supply. Electrons then flow back from the negatively charged plate towards the positively charged plate.
Discharging (capacitor): The process in which stored charge leaves the capacitor plates through an external circuit, causing the potential difference and current to decrease over time.
At the beginning of discharge, the current is at its maximum because the potential difference across the capacitor is greatest. Over time:
The capacitor’s stored charge falls.
Its potential difference declines.
The current decreases, approaching zero as the capacitor empties of charge.
EQUATION
—-----------------------------------------------------------------
Capacitor Discharging (Charge) = Q(t) = Q₀ e^(−t/RC)
Q(t) = Charge on capacitor at time t (coulombs, C)
Q₀ = Initial charge on capacitor (coulombs, C)
t = Time since discharging began (seconds, s)
R = Resistance (ohms, Ω)
C = Capacitance (farads, F)
—-----------------------------------------------------------------
This exponential decay ensures that the discharge slows continuously, never dropping to zero instantly but approaching it asymptotically.
Predicting Current, Voltage, and Charge Changes
A resistor–capacitor circuit allows precise prediction of how quantities evolve.
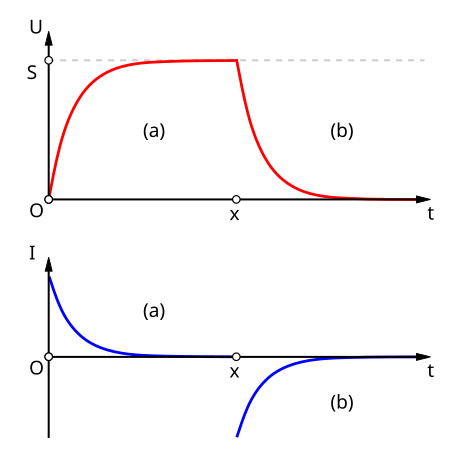
This figure displays how capacitor voltage and current vary during both charging and discharging in a resistor–capacitor circuit. It highlights the exponential rising and falling behaviour referenced in the notes. Additional labels such as “S” for saturation exceed syllabus requirements but do not hinder interpretation. Source.
The exponential behaviour means that the rate of change at any moment is proportional to the quantity still remaining to change.
Charging Trends
Charge Q increases, approaching its maximum asymptotically.
Voltage V increases, matching the shape of the charge curve.
Current I decreases, starting high and falling rapidly as the capacitor fills.
Discharging Trends
Charge Q decreases, halving at constant time intervals characteristic of exponential decay.
Voltage V decreases, mirroring the charge curve.
Current I decreases, beginning large and falling towards zero.
Reasons for These Trends
As the capacitor charges, electrostatic repulsion builds up on the plate receiving electrons, resisting further electron flow.
The resistor limits current at all times, controlling the rate of change.
When discharging, the capacitor acts as a temporary power supply, driving current through the resistor until its stored energy is exhausted.
The Circuit Perspective
Analysing a resistor–capacitor (RC) circuit highlights key ideas essential for this subsubtopic.
When Charging
The supply provides energy to move electrons onto one plate.
The resistor drops part of the supply voltage, leaving the remainder to appear across the capacitor.
Over time, the capacitor’s voltage rises while the resistor’s voltage falls.
When Discharging
The capacitor itself becomes the energy source.
Current direction reverses relative to the charging situation.
The resistor dissipates the capacitor’s stored energy as heat.
Key Features of RC Transients
Recognising the essential characteristics of charge and discharge processes is vital for circuit interpretation.
The initial current is always maximum during charging or discharging because the potential difference driving the current is largest at this point.
The final current is zero because the capacitor behaves as an open circuit once fully charged or fully discharged.
All changes follow exponential laws, a hallmark of RC circuits.
The resistor determines how quickly or slowly the capacitor approaches its final state.
These principles create the foundation for understanding more complex transient behaviour and form the core of the specification requirement to explain and predict changes in charge, voltage, and current in resistor–capacitor circuits.
FAQ
The rate is controlled by the product of resistance and capacitance, known as the RC value. A larger resistance slows current flow, while a larger capacitance requires more charge to change the potential difference.
Higher RC values result in slower charging and discharging because the circuit takes longer to move enough charge to significantly alter the potential difference across the capacitor.
During charging, the current flows from the power supply, forcing electrons onto one plate and creating charge separation.
During discharging, the capacitor effectively becomes the source, releasing its stored energy. Electrons then move in the opposite direction, driven by the potential difference that now resides across the capacitor plates.
Yes. A capacitor holding more energy (i.e., at a higher initial potential difference) produces a larger initial current when discharged through a resistor.
As the energy dissipates as heat in the resistor, the potential difference across the capacitor falls, causing the current to diminish. The shape of the energy decay mirrors the exponential decline of charge and voltage.
These factors influence the capacitance, which alters how much charge is required to reach a given potential difference.
Increased plate separation reduces capacitance, leading to faster voltage rise or fall for a given current.
A higher-permittivity dielectric increases capacitance, slowing the voltage change because more charge must be transferred.
The resistor behaviour remains the same, but the capacitor’s characteristics adjust the time evolution of the circuit.
Instantaneous change would require infinite current, which is impossible in a real circuit containing resistance. The resistor limits how fast electrons can move.
As the capacitor’s potential difference builds or falls, the driving force behind current flow reduces, making the process progressively slower. This is why the approach to final values is asymptotic rather than abrupt.
Practice Questions
Question 1 (2 marks)
A capacitor is connected in series with a resistor to a DC power supply. At the moment the circuit is switched on, the current is at its maximum value.
Explain why the current is initially maximum and describe how it changes as the capacitor charges.
Question 1 (2 marks)
1 mark: States that initially the potential difference across the capacitor is zero (or the capacitor is uncharged).
1 mark: Explains that as the capacitor charges, its potential difference increases and therefore the current decreases from its initial maximum value.
Question 2 (5 marks)
A capacitor of fixed capacitance is fully charged and then discharged through a resistor.
Describe in detail how the charge, potential difference across the capacitor, and current in the circuit change during the discharge process.
In your answer, refer to the shape of the graphs you would expect for each quantity and the physical reasons for these changes.
Question 2 (5 marks)
1 mark: Charge on the capacitor decreases over time.
1 mark: Potential difference across the capacitor decreases over time, following the same exponential trend as charge.
1 mark: Current in the circuit decreases from a maximum value towards zero.
1 mark: States that all three quantities decrease exponentially (or describes the curve shape: rapid fall initially, then gradually flattening).
1 mark: Explains that the decreasing potential difference across the capacitor reduces the driving force for current, causing the current to diminish as discharge progresses.

