The time constant is a central concept in analysing capacitor–resistor circuits, revealing how voltage, charge, and current change over time during charging and discharging processes.

The Concept of the Time Constant in Capacitor–Resistor Circuits

The time constant describes how rapidly a capacitor in a circuit with a resistor will either charge or discharge. It allows physicists and engineers to predict how the system evolves without directly solving the exponential equations each time. For OCR A-Level Physics, understanding the time constant involves defining the quantity τ, calculating it using circuit values, and interpreting what this value means physically when observing capacitor behaviour.

A simple series RC circuit consisting of a DC source, a resistor R, and a capacitor C. The same arrangement is used when defining the time constant τ = RC. This diagram focuses only on the essential components, matching the level of detail required for OCR A-Level Physics. Source.

The importance of this definition becomes clearer when examining capacitor transients, where the shape and steepness of exponential curves depend directly on τ. This single parameter provides a concise way to describe the system’s responsiveness.

EQUATION
—-----------------------------------------------------------------
Time Constant (τ) = RC
R = Resistance of the resistor in ohms (Ω)
C = Capacitance of the capacitor in farads (F)
—-----------------------------------------------------------------

A larger time constant means the capacitor charges or discharges more slowly, while a smaller one means the process occurs more rapidly. This relationship makes τ fundamental when designing circuits that rely on controlled timing, such as filters, timing circuits, or sensors.

Physical Significance of the Time Constant

The physical significance of τ lies in how it determines the fraction of charge or voltage lost—or gained—during each equal time interval. Capacitor charge or potential difference does not fall linearly but instead follows exponential decay or growth. This behaviour means that the time constant represents a key milestone in the capacitor’s evolution.

After a time equal to one time constant (τ):
• A discharging capacitor will have reduced to approximately 37% of its initial charge or potential difference.
• A charging capacitor will have reached approximately 63% of its maximum charge or potential difference.

These values arise naturally from exponential relationships and are not arbitrary thresholds.

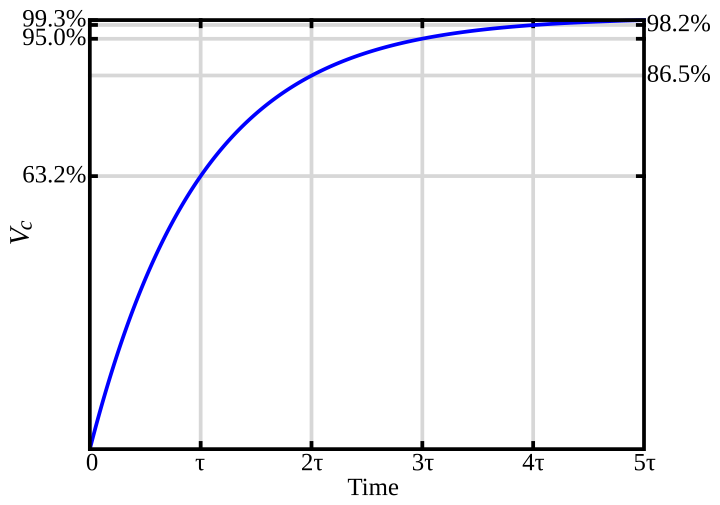
Voltage across a capacitor in a series RC circuit as it charges with time. The curve shows the exponential approach to the final voltage, with the point at one time constant τ highlighted at about 63% of the maximum. The graph reinforces that τ characterises how quickly the capacitor’s voltage rises. Source.

Understanding τ During Charging and Discharging

During charging, electrons are removed from one plate and accumulate on the other. As the capacitor approaches its maximum charge, the rate of electron movement slows. The time constant dictates how quickly this slowing becomes substantial.
During discharging, electrons flow back through the resistor to equalise charge between plates. Again, the rate decreases with time, and τ determines the steepness of this decline.

Key features governed by the time constant include:
• Rate of voltage change across the capacitor
• Rate of current change through the resistor
• Time required for significant portions of charge to build up or decay
• Shape and steepness of exponential curves

These features are central in analysing transient behaviour, making τ invaluable when evaluating how a system responds to switching events or sudden changes.

Interpreting τ in Real Circuits

OCR requires not only defining τ = RC but also interpreting its physical significance. Students should be able to link the mathematical form to observable effects in real circuits. A time constant can be understood as the characteristic “reaction time” of a capacitor–resistor system.

A circuit with:
• High resistance slows current flow, increasing τ
• Large capacitance requires more charge to change voltage, also increasing τ
• Low resistance or capacitance reduces τ, making the system respond quickly

Bullet points for interpretation:
• τ provides a benchmark for when significant change occurs in the capacitor’s electrical state.
• Observing a system for several multiples of τ helps determine when a capacitor is effectively fully charged or discharged.
• Circuit designers adjust R or C deliberately to control timing behaviour.
• τ allows prediction of system responsiveness without plotting full exponential curves.

Practical Considerations When Working with τ

When measuring or analysing circuits involving capacitors and resistors, recognising the influence of the time constant improves both accuracy and interpretation. Practical circuit work often involves using meters or data-loggers, and understanding τ helps ensure that recorded values are taken at sensible intervals.

Important practical points include:
• When τ is small, data must be recorded rapidly to capture early steep changes.
• When τ is large, measurements should span a longer period to capture the full trend.
• Knowing τ helps decide appropriate time scales for oscilloscope traces.
• Intervals of equal length allow easy comparison of how exponential decay progresses relative to τ.

By connecting these practical steps to the concept of τ, students strengthen their ability to analyse capacitor behaviour effectively.