OCR Specification focus:
‘Apply Coulomb’s law: F = (1/(4πɛ0)) · (Qq / r²) for the force between two point charges.’
Electric forces between charged particles underpin many electrical phenomena. Understanding how two point charges interact allows students to analyse electrostatic behaviour, predict forces, and appreciate fundamental physical symmetries in electric fields.
The Nature of Electrostatic Interaction
Electrostatic forces arise because objects possess electric charge, a fundamental property that causes them to experience attraction or repulsion. When the charges are sufficiently small or separated so that their actual size is negligible, each can be modelled as a point charge, simplifying the analysis of their interaction.
Point Charges and the Electric Force
A point charge behaves as if all its charge were concentrated at a single point in space, meaning the force between two such charges depends only on their magnitudes and the distance between them. According to the specification, students must apply Coulomb’s law, which quantifies this force precisely and forms the foundation of electrostatic calculations.
EQUATION
—-----------------------------------------------------------------
Coulomb’s Law (F) = (1/(4πɛ₀)) · (Qq / r²)
F = Electrostatic force between two point charges (newtons, N)
Q = Charge on the first point charge (coulombs, C)
q = Charge on the second point charge (coulombs, C)
r = Separation between the charges (metres, m)
ɛ₀ = Permittivity of free space, a constant defining how electric fields propagate in vacuum (farads per metre, F m⁻¹)
—-----------------------------------------------------------------
This law quantitatively links the force to the charges and their separation while incorporating the medium between them through ɛ₀, which determines how strongly electric fields interact in free space.
Characteristics of the Electrostatic Force
The force described by Coulomb’s law shares several core features important for OCR A-Level Physics understanding.
Magnitude and Direction
The magnitude of the force is determined by the equation above, but its direction depends on the signs of the interacting charges.
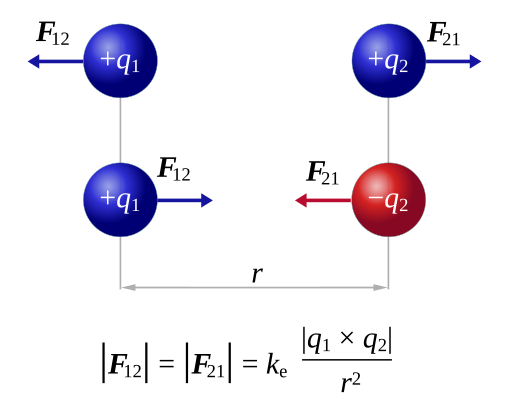
Diagram of two point charges illustrating Coulomb’s law. Like charges repel and unlike charges attract; in both cases the forces are equal in magnitude and opposite in direction along the line joining the charges. Source.
Students should clearly understand the following behaviours:
Like charges repel — two positive or two negative charges create a force pushing them apart.
Unlike charges attract — a positive and a negative charge experience a force drawing them together.
The force always acts along the line joining the charges, making it a central, radial force.

Two-panel figure showing point charges separated by distance rrr. In (a) like charges repel; in (b) unlike charges attract; in both, the forces on each charge are equal and opposite along the line of centres. Source.
The Inverse-Square Relationship
A particularly important aspect of Coulomb’s law is its inverse-square dependence on separation, which means:
Doubling the separation reduces the force to one quarter.
Halving the separation increases the force to four times its original value.
This inverse-square law mirrors other fundamental physical interactions, such as gravitational forces, and reflects how field strength diminishes as it spreads through three-dimensional space.
The Role of the Medium and the Constant 1/(4πɛ₀)
The constant 1/(4πɛ₀) appears in the standard SI form of Coulomb’s law because it expresses how electric fields behave in a vacuum. The permittivity ɛ₀ characterises the “electrical resistance” of free space to electric field formation and determines how strongly two charges interact.
Although this subsubtopic focuses on forces in free space, OCR students should recognise that real materials introduce modified permittivity values. However, those considerations belong to later parts of the topic and do not alter the core free-space form required here.
Representing Electrostatic Forces
Electrostatic forces are vector quantities, meaning they have magnitude and direction. When multiple charges are present, forces combine using vector addition, but this subsubtopic focuses solely on the interaction between two point charges.
Important Features When Analysing Forces
Understanding the following principles helps interpret Coulomb’s law clearly:
The force on charge Q due to charge q is equal in magnitude and opposite in direction to the force on q due to Q, consistent with Newton’s third law.
Only the distance between charge centres matters; charge distribution details are ignored when using a point model.
The law applies in classical electrostatics where charges are stationary or moving slowly enough that magnetic effects are negligible.
Using Coulomb’s Law in Practice
Although no worked examples are included here, students must be prepared to use Coulomb’s law numerically and conceptually.
Key Steps When Applying the Law
Identify the two interacting point charges and assign them values Q and q.
Measure or determine the separation r between their centres.
Substitute into the Coulomb’s law equation, ensuring consistent SI units.
Determine whether the resulting force is attractive or repulsive based on the signs of the charges.
Represent the force directionally along the line joining the charges.
A clear grasp of these steps supports the correct and confident use of Coulomb’s law, as required by the OCR specification.
Visualising the Force Between Charges
Although Coulomb’s law is mathematical, visual reasoning enhances comprehension:
The force vector always lies on the straight line between the charges.
Increasing charge magnitude makes the force stronger; decreasing separation increases it dramatically due to the inverse-square relationship.
Attractive and repulsive interactions produce opposite vector directions but follow the same mathematical form.
Such visualisations help relate the algebraic expression to physical intuition, reinforcing understanding of how electrostatic interactions shape the behaviour of charged particles.
Importance of Coulomb’s Law in Physics
Coulomb’s law is fundamental because it provides the first quantitative link between charge, distance, and electric force. It forms the basis for analysing electric fields, potential, and energy in later subsubtopics and connects deeply to many theoretical and practical areas of physics.
FAQ
Coulomb’s law assumes that all charge can be treated as concentrated at a single point. This works when the object is extremely small compared with the separation or when the charge is distributed uniformly over a sphere.
For irregular shapes or non-uniform charge distributions, the electric field varies across the surface, so the simple point-charge model no longer applies. In such cases, the force must be calculated by integrating contributions from each small element of charge.
Nearby conductive objects can distort electric fields because charges within the conductor redistribute, altering the field lines around the point charges.
This effect can either increase or decrease the net force depending on the geometry and position of the conducting surface. Insulators have a weaker influence, but polarisation within the material can still slightly modify the effective force.
This constant arises from the way electric fields spread out in three-dimensional space. It reflects the geometric factor associated with spherical symmetry, linking field strength to area over which field lines spread.
It also embeds the permittivity of free space, setting the strength of electric interactions in a vacuum. Different media replace epsilon0 with a modified permittivity, changing the magnitude of the force.
Because the force is proportional to the product Qq, doubling one charge and halving the other leaves the product unchanged.
Therefore, the overall force stays the same in magnitude, though its direction still depends on whether the charges are like or unlike. This demonstrates the symmetry of the force-charge relationship in Coulomb’s law.
Coulomb’s law produces forces that are equal in magnitude and opposite in direction because the field created by each charge acts on the other independently. The magnitudes match because both forces arise from the same pair of charges separated by the same distance.
This occurs regardless of whether Q and q have different values, ensuring action and reaction remain balanced in compliance with Newton’s third law.
Practice Questions
Question 1 (2 marks)
State Coulomb’s law for the force between two point charges and describe how the direction of this force depends on the signs of the charges.
Mark scheme:
• States that the force between two point charges is proportional to the product of the charges and inversely proportional to the square of the distance between them, or gives the equation F = (1/(4 pi epsilon0)) (Qq / r^2). (1 mark)
• States that like charges repel and unlike charges attract, or correctly describes the direction of the force depending on charge signs. (1 mark)
Question 2 (5 marks)
Two point charges are held a fixed distance apart in free space. Explain how the magnitude of the electrostatic force between them depends on:
(a) the magnitudes of the two charges,
(b) the separation between them,
(c) the sign of each charge, and
(d) the properties of the medium between them.
Your answer should refer to the form of Coulomb’s law and the physical behaviour it represents.
Mark scheme:
Award marks for any five of the following distinct points:
• States that the force increases when either charge increases, proportional to the product Qq. (1 mark)
• States that the force decreases with the square of the distance between the charges, following an inverse-square relationship. (1 mark)
• States that like charges give a repulsive force and unlike charges give an attractive force, with the force acting along the line joining the charges. (1 mark)
• Explains that the force depends on the medium through the permittivity term (epsilon0 in free space). (1 mark)
• Correctly references the form F = (1/(4 pi epsilon))(Qq / r^2) when describing the dependence on charge, distance, and medium. (1 mark)

