OCR Specification focus:
‘Use E = V/d for a uniform electric field between parallel plates.’
A uniform electric field provides a consistent force on charged particles and serves as a vital idealised model for analysing motion, energy changes, and field behaviour in many physics contexts.
Understanding Uniform Electric Fields
A uniform electric field is a region in which the electric field strength has the same magnitude and direction at every point. This type of field is typically produced between two large, parallel, conducting plates that are separated by a small distance and maintained at a constant potential difference. In such configurations, the field lines are straight, parallel, and evenly spaced, indicating uniformity.
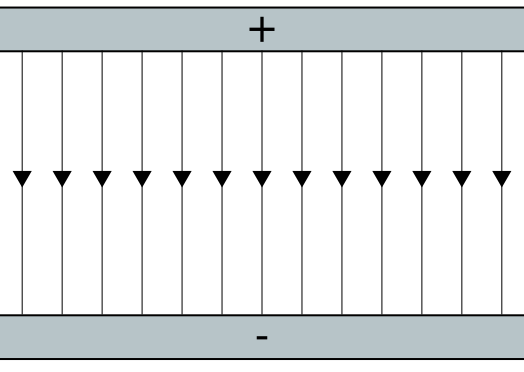
Uniform electric field between large parallel plates. Field lines are parallel and equally spaced, indicating constant magnitude and direction throughout the central region. Small edge fringing at the plate ends is typically neglected at A-Level. Source.
Because the field strength is constant, uniform fields allow simplified analysis of how charges behave under electric forces. This subsubtopic focuses on the relationship between the electric field strength, the potential difference across the plates, and the separation between the plates.
When students first encounter uniform electric fields, it is important to recognise that the model assumes ideal conditions. Edge effects—regions near the plate boundaries where the field becomes non-uniform—are ignored for the purposes of A-Level calculations.
Electric Field Strength in a Uniform Field
The key OCR requirement for this subsubtopic is the use of the electric field strength equation that relates potential difference and plate separation. Electric field strength describes how strongly a field acts on a positive test charge placed within it.
Electric field strength: The force per unit positive charge acting at a point in an electric field.
In a uniform field, the electric field strength has a simple and direct relationship with the voltage applied across the plates and the distance between them. The stronger the potential difference, or the smaller the separation, the greater the field strength becomes. This relationship underpins much of the practical and theoretical analysis involving parallel-plate systems such as capacitors, cathode-ray tubes, and particle accelerators.
EQUATION
—-----------------------------------------------------------------
Electric Field Strength (E) = V / d
E = Electric field strength, measured in volts per metre (V m⁻¹)
V = Potential difference across the plates, measured in volts (V)
d = Separation between the plates, measured in metres (m)
—-----------------------------------------------------------------
This formula is central to the OCR A-Level requirement “Use E = V/d for a uniform electric field between parallel plates,” and students must be confident in applying it in various conceptual and quantitative contexts.
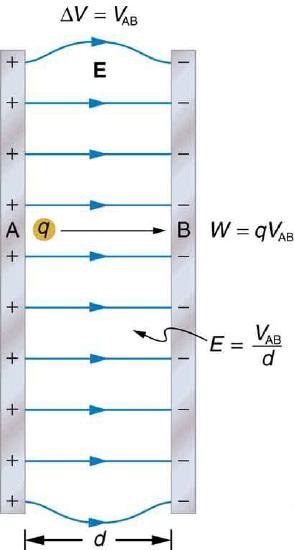
Relationship between potential difference and field in parallel plates with E = V/d. Plates A (positive) and B (negative) are separated by distance d, and field lines run uniformly from A to B. The diagram also shows work/energy notation (W = qV_AB), which exceeds this subsubtopic but can be ignored here. Source.
The equation shows that electric field strength increases proportionally with potential difference and decreases when the plates are further apart.
Characteristics of Field Lines in Uniform Fields
Field lines are a visual representation of how a field behaves and remain a core concept when studying uniform fields. Although this subsubtopic does not explicitly require detailed mapping of field lines, understanding their appearance supports comprehension of uniformity:
They are parallel, indicating that the direction of the force on a positive test charge is the same throughout the region.
They are equally spaced, showing that the magnitude of the field is constant.
They point from the positively charged plate to the negatively charged plate.
This representation contrasts with point-charge fields, where lines converge or diverge and field strength varies with distance. The predictability of uniform fields makes them especially useful in theoretical modelling.
Potential Difference and Work in Uniform Fields
The relationship E = V/d links the energy considerations of moving charges to their spatial environment. As potential difference represents work done per unit charge, the uniform field strength indicates how much electrical energy changes per metre of displacement in the field’s direction.
A positive charge moving in the direction of the field loses electrical potential energy, while a negative charge moving in the same direction gains energy. This consistent rate of energy change per metre is a defining feature of uniform fields. It enables students to predict motion and energy transformations without needing more complex position-dependent equations.
Forces on Charges in Uniform Fields
Although the mathematical treatment of particle motion appears in a later subsubtopic, it is still necessary to recognise how uniform field strength relates to the force experienced by charges. Once the field strength is known, the force on a charge is given by F = E q, but this relationship is not the primary focus of subsubtopic 20.3.1. Instead, students need to appreciate that a constant electric field produces a constant electric force, underpinning uniform acceleration for charged particles.
Important points regarding force in uniform fields include:
The force direction on a positive charge is along the field lines.
The force direction on a negative charge is opposite to the field lines.
A constant force results in constant acceleration, provided no other forces act.
These ideas become essential when applying E = V/d to real situations involving particle dynamics.
Applying the Uniform Field Model
Uniform fields are encountered in many physical systems. They appear in laboratory equipment, industrial applications, and theoretical models used to simplify complex interactions. Their predictability and the clear proportionalities between voltage, distance, and field strength enable precise control of charged particle motion.
Students should understand the following typical uses of the uniform field model:
Designing and analysing parallel-plate capacitors.
Understanding electron acceleration in vacuum tubes.
Modelling ion motion in mass spectrometers.
Explaining how droplets, dust particles, or aerosols respond to controlled electric forces.
Although later subsubtopics expand upon capacitor structure and charged particle motion, subsubtopic 20.3.1 focuses directly on the relationship between electric field strength, plate separation, and potential difference, forming the foundation for these later applications.
The ability to apply E = V/d confidently ensures groundwork for analysing numerous uniform-field scenarios, making this subsubtopic fundamental for progressing through the wider field-related content in A-Level Physics.
FAQ
A practical check for uniformity involves measuring potential at several points between the plates using a probe connected to a voltmeter. If the field is uniform, equal changes in position along a straight line between the plates produce equal changes in potential.
Equipotential lines can also be mapped using conducting paper.
• Straight, evenly spaced equipotentials indicate a uniform electric field.
• Any curvature or irregular spacing shows regions where the field is not uniform.
Larger plates create a wider central region where edge effects have minimal influence, improving field uniformity.
If the separation between plates is small relative to their size, fringing fields form only near the edges.
• Increasing plate separation reduces the proportion of the field that is uniform.
• Reducing plate separation improves uniformity but increases the likelihood of electrical breakdown at high voltages.
Manufacturing imperfections, slight misalignment, and variation in plate surface quality introduce small non-uniformities.
Other factors include:
• Fringing at plate edges
• Dust, moisture, or contamination altering local conductivity
• Uneven contact with the voltage supply
• Air ionisation at high voltages affecting local field strength
These effects are usually minor, but high-precision experiments compensate for them.
In the basic OCR formula E = V/d, the medium is assumed to be air or vacuum. Changing the medium affects breakdown voltage and the behaviour of charges within the field, even though the geometric relationship remains the same.
Different media can:
• Allow higher operating voltages without sparking
• Alter how particles move through the field
• Influence charge leakage across or along the plates
Dielectrics are studied more formally in later subtopics, but their presence still matters for uniform-field applications.
By convention, electric field direction is defined as the direction a positive test charge would move if placed in the field.
Because a positive charge is repelled by the positive plate and attracted to the negative plate, field lines between parallel plates point from the positive plate to the negative one.
This convention ensures consistency when predicting the motion of charged particles and analysing electric forces in uniform fields.
Practice Questions
Question 1 (2 marks)
A pair of large parallel metal plates is connected to a power supply producing a potential difference of 60 V. The plates are separated by 0.020 m.
(a) State the equation used to calculate the electric field strength between the plates.
(b) Calculate the electric field strength.
Mark scheme:
(a) 1 mark
• States E = V/d.
(b) 1 mark
• Correct calculation: E = 60 / 0.020 = 3000 V m⁻¹ (allow 3.0 × 10³ V m⁻¹).
Question 2 (5 marks)
A beam of positively charged particles enters a region containing a uniform electric field between two parallel plates.
(a) Explain why the electric field in the central region between the plates can be considered uniform.
(b) Describe and explain the motion of the positively charged particles as they travel through the uniform field.
(c) Using the relationship E = V/d, explain how increasing the potential difference between the plates affects the motion of the particles.
Mark scheme:
(a) 1 mark
• Field lines between large, closely spaced plates are straight, parallel, and equally spaced.
• Edge effects are small and can be ignored in the central region (any one for 1 mark).
(b) 2 marks
• Positively charged particles experience a force in the direction of the electric field. (1 mark)
• Particles undergo constant acceleration because the field (and therefore force) is uniform. (1 mark)
(c) 2 marks
• Increasing V increases the electric field strength because E = V/d. (1 mark)
• Greater field strength increases the force on each particle, resulting in greater acceleration and a larger deflection. (1 mark)

