OCR Specification focus:
‘For a particle at right angles to B, F = B Q v gives magnetic force magnitude.’
A charged particle moving through a magnetic field experiences a force dependent on its velocity, charge, and the field strength, influencing its motion in predictable ways.
Understanding the Magnetic Force on a Moving Charge
When a charged particle travels through a magnetic field, the field interacts with the particle’s motion, producing a force often called the magnetic force or Lorentz force (magnetic component). This force is central to many physical systems, from particle accelerators to mass spectrometers, and is essential knowledge for OCR A-Level Physics.
Magnetic field: A region in which a moving charge or current experiences a force.
The specification focuses specifically on the case where the velocity of the particle is perpendicular to the magnetic field lines, leading to the commonly used relationship between magnetic flux density, charge, velocity, and force.
The Nature of Magnetic Interaction with Moving Charges
A magnetic field exerts no force on a stationary charge. The force arises only when the charge has motion relative to the field, and its magnitude depends on the orientation of that motion. When the velocity is at right angles to the field direction, the force reaches its maximum value.
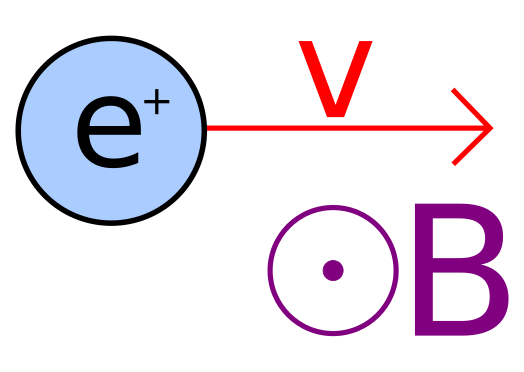
A positron moves through a uniform magnetic field, showing that the magnetic force acts perpendicularly to both velocity and magnetic field direction. Extra vectors shown reflect geometric relationships beyond the syllabus requirement but reinforce the perpendicular-force concept. Source.
Factors Affecting the Magnetic Force
The magnetic force on a moving charge depends on three key quantities:
Magnetic flux density (B) — the strength of the magnetic field
Charge (Q) — the electric charge of the particl
Velocity (v) — the speed of the particle when it moves perpendicular to the field
The force is always perpendicular to both the velocity and the magnetic field, resulting in motion that is commonly circular or curved.
Expression for Force at Right Angles
For the case specified by the OCR syllabus—motion at right angles to the field—the magnetic force magnitude is given by the following relationship.
EQUATION
—-----------------------------------------------------------------
Magnetic Force on a Moving Charge (F) = B Q v
B = Magnetic flux density, measured in tesla (T)
Q = Charge of the particle, measured in coulombs (C)
v = Velocity of the particle perpendicular to the field, measured in metres per second (m s⁻¹)
—-----------------------------------------------------------------
This relationship highlights that the magnetic force increases linearly with each variable.
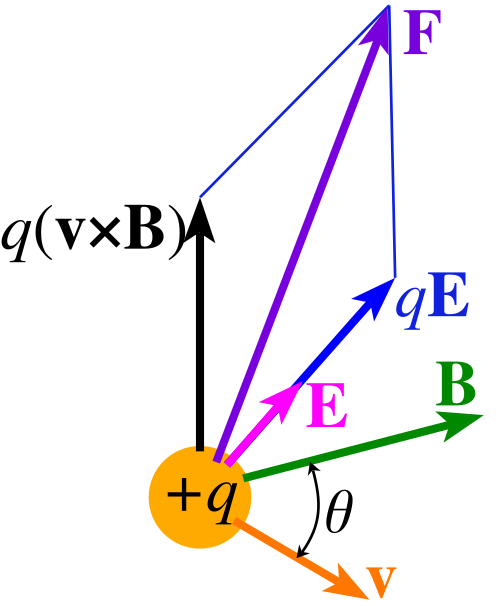
A diagram illustrating the Lorentz force acting on a charged particle. The magnetic contribution to the force is perpendicular to both velocity and magnetic field. The electric field component included exceeds the requirements for this subsubtopic but helps visualise the full force context. Source.
The magnetic force does not do work because it acts perpendicularly to the direction of motion. Work requires a component of force along the direction of displacement, so the magnetic component cannot change the particle’s kinetic energy.
Direction of the Magnetic Force
The direction of the force is governed by the left-hand rule for charges, reflecting the vector nature of the magnetic interaction. For a positively charged particle, the force direction follows the conventional left-hand rule, whereas a negatively charged particle experiences a force in the opposite direction.
Lorentz force (magnetic component): The force experienced by a moving charge due to its interaction with a magnetic field.
This means that the direction of force is determined by:
Thumb → direction of motion of the positive charge
First finger → direction of the magnetic field
Second finger → direction of magnetic force
A negative charge simply reverses the force direction.
The perpendicular relationship between velocity, magnetic field, and magnetic force is a key part of understanding charged-particle dynamics.
How Force Influences Motion
Because the magnetic force is always perpendicular to the velocity, it alters the direction of motion without changing speed. This results in curved trajectories, with circular motion being the most common outcome for the perpendicular case highlighted in this subsubtopic.
Key Effects of the Magnetic Force
The force can:
Deflect charged particles in devices such as cathode-ray tubes
Produce circular or spiral paths in magnetic fields
Control ion trajectories in particle accelerators
Separate ions of different mass and charge in mass spectrometers
Each of these applications relies on the predictable magnitude of the magnetic force when velocity is perpendicular to the field.
A charged particle that enters a magnetic field at right angles continues at a constant speed but its direction changes continuously, giving rise to uniform circular motion governed by centripetal force considerations.
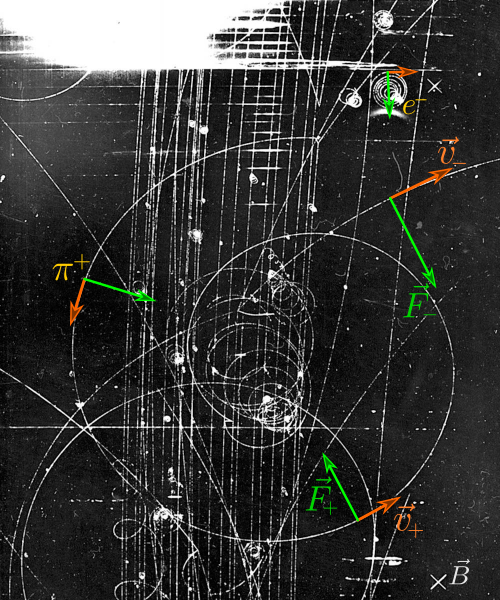
Bubble-chamber tracks demonstrating the curvature of charged-particle paths in a magnetic field. Opposite charge signs bend in opposite directions under the perpendicular magnetic force. Additional particle interactions visible exceed syllabus requirements but clearly illustrate magnetic deflection. Source.
Practical Contexts
The relationship F = B Q v is often exploited in several practical contexts within physics and engineering:
Particle acceleration: Charged particles are bent into circular paths using magnetic fields.
Mass spectrometry: Particles of different mass-to-charge ratio follow different radii.
Cathode-ray tubes: Electron beams are deflected to create images.
Fusion research: Plasma in magnetic confinement devices moves under magnetic forces.
Understanding the force on a moving charge provides a foundation for studying these devices and technologies.
FAQ
The magnetic force has the same magnitude for particles with equal speed, charge magnitude, and field strength, but its direction is reversed for negative charges.
For a positive charge, the force follows the conventional left-hand rule.
For a negative charge, the force is in the opposite direction because the charge value is negative.
This opposite curvature is why electron beams curve differently from proton beams in the same magnetic field.
The magnetic force is always perpendicular to the direction of motion. Work requires a force component parallel to displacement, so no energy is transferred.
This means that while the magnetic field can change the direction of the particle, it cannot change its speed or kinetic energy.
Any change in speed must come from electric fields or collisions, not from magnetic interactions.
The velocity can be split into two components:
• A perpendicular component, which causes circular motion
• A parallel component, which remains unaffected
The result is helical motion, with the particle spiralling around the field lines while drifting forward along them.
The pitch of the helix depends on the relative sizes of the perpendicular and parallel components of velocity.
A larger charge experiences a larger magnetic force for the same speed and field strength.
A stronger force increases the particle’s curved deflection, producing a smaller radius of curvature.
Conversely, particles with smaller charges curve less and travel in larger-radius paths, which is a principle used in separating ions of different charge in experimental setups.
When the velocity is perpendicular to the magnetic field, the magnetic force acts exactly as a centripetal force.
The magnitude of the force remains constant because:
• The speed stays constant
• The field strength stays constant
• The force depends only on B, Q, and v
Because the force continually redirects the velocity without changing its magnitude, uniform circular motion naturally results in a uniform magnetic field.
Practice Questions
Question 1 (2 marks)
A positively charged particle moves at right angles to a uniform magnetic field. State the expression for the magnetic force acting on the particle and describe the direction of this force.
Question 1 (2 marks)
• States the expression F = B Q v (1)
• States that the force is perpendicular to both the velocity of the particle and the magnetic field / follows the appropriate left-hand rule direction (1)
Question 2 (5 marks)
A beam of electrons enters a region of uniform magnetic field at right angles to the field lines.
(a) Explain why the electrons follow a circular path in the magnetic field.
(b) Describe how increasing the speed of the electrons affects the radius of their circular path.
(c) State one practical application that relies on the deflection of charged particles by magnetic fields.
Question 2 (5 marks)
(a)
• Magnetic force acts perpendicular to the velocity of the electrons (1)
• This provides the centripetal force needed for circular motion (1)
(b)
• Increasing speed increases the radius of the circular path (1)
• Because a greater centripetal force is required to maintain tighter curvature / magnetic force remains the same for fixed B and charge but momentum increases (1)
(c)
• States a valid application such as a mass spectrometer, cathode-ray tube, particle accelerator, or similar device relying on magnetic deflection (1)

