OCR Specification focus:
‘Describe circular orbits of charges in uniform magnetic fields and relate to dynamics.’
Charged particles travelling through a uniform magnetic field experience a force that continually redirects their motion, creating circular trajectories governed by electromagnetic interactions and Newtonian dynamics.
Circular Motion of Charged Particles
Charged particles moving through a magnetic field form a central part of electromagnetism. When the velocity of a charged particle is perpendicular to the magnetic field, it experiences a force that is always at right angles to its motion, causing it to follow a circular path.
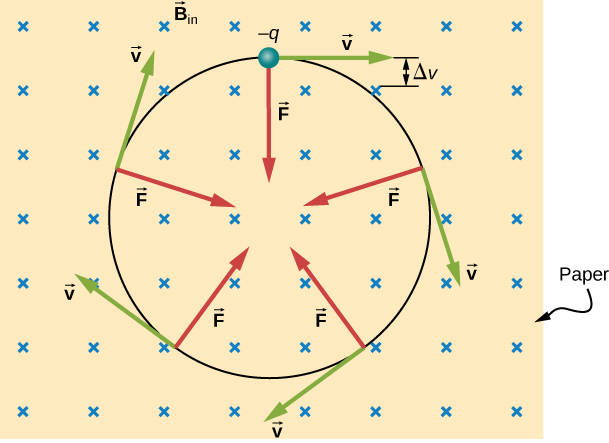
Uniform circular motion of a negatively charged particle in a uniform magnetic field directed into the page. The diagram shows the velocity tangent to the circular path and the magnetic force always directed toward the centre, providing centripetal force. Extra contextual detail included is the note that force direction reverses because the charge is negative. Source.
This circular motion is fundamental to technologies such as cyclotrons, mass spectrometers, and particle detectors, as well as to natural systems such as the motion of ions in Earth’s magnetic field.
The Magnetic Force as a Centripetal Force
A charged particle moving with velocity v through a uniform magnetic field B experiences the magnetic force, often termed the Lorentz force. This force always acts perpendicularly to both the velocity and the magnetic field direction, so it does not change the particle’s speed, only its direction. This behaviour ensures that the force provides the centripetal component necessary for uniform circular motion.
Lorentz Force: The force experienced by a charged particle moving in a magnetic field, acting perpendicular to its velocity and the magnetic field.
Because the magnetic force is always perpendicular to the velocity, no work is done on the particle, and its kinetic energy remains constant. This distinctive characteristic is central to understanding circular motion in magnetic fields.
Magnetic Force Magnitude
For a charged particle travelling at right angles to a magnetic field, the magnitude of the magnetic force is given by a simple relation that OCR students must be familiar with.
EQUATION
—-----------------------------------------------------------------
Magnetic Force (F) = B Q v
F = Magnetic force in newtons (N)
B = Magnetic flux density in tesla (T)
Q = Charge of the particle in coulombs (C)
v = Velocity of the particle in metres per second (m s⁻¹)
—-----------------------------------------------------------------
The existence of this force ensures that the particle is constantly deflected, giving rise to circular motion whose characteristics depend on the particle’s charge, mass, speed, and the magnetic field strength.
A charged particle in circular motion maintains constant speed but undergoes continuous acceleration towards the centre of the circular path. This acceleration is the centripetal acceleration, required for any object undergoing uniform circular motion.
Relating Magnetic Force to Centripetal Dynamics
The dynamics of circular motion emerge when the magnetic force is equated to the centripetal force required to maintain circular motion.
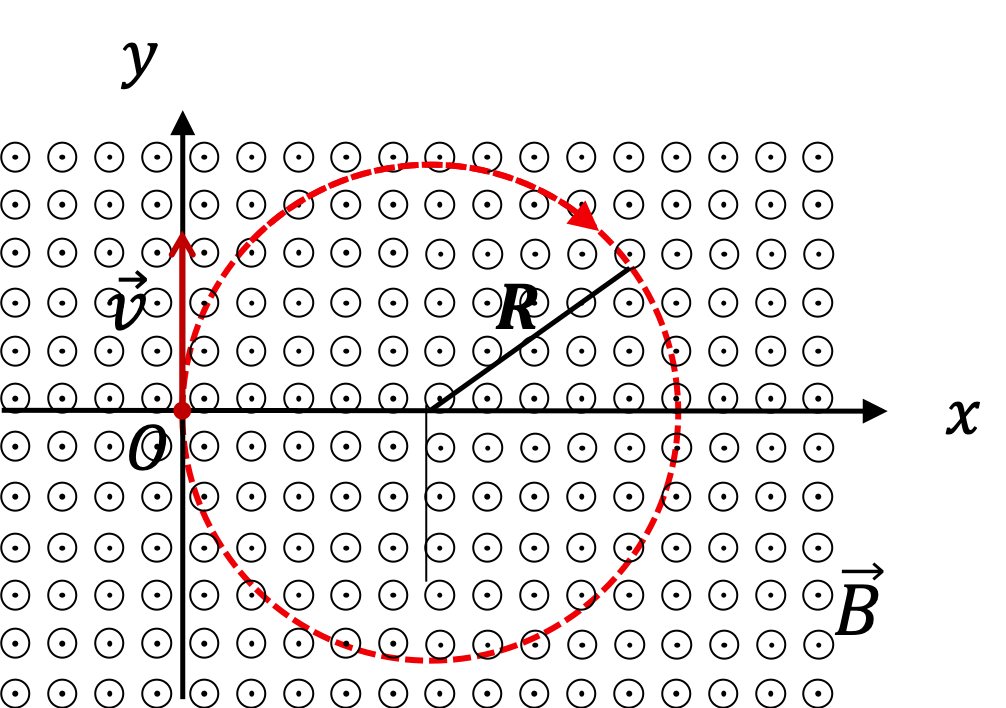
Circular motion of a positive charge in a uniform magnetic field, with the centripetal force supplied by the magnetic force. The particle moves in a circular path of radius R, with the magnetic force constantly directed toward the centre. Extra detail included is the explicit relation mv²/R = QvB, linking the magnetic and centripetal force expressions. Source.
This relationship allows us to determine the radius of the circular path and the period of revolution.
EQUATION
—-----------------------------------------------------------------
Centripetal Force (F) = m v² / r
m = Mass of the particle in kilograms (kg)
v = Velocity of the particle in metres per second (m s⁻¹)
r = Radius of circular path in metres (m)
—-----------------------------------------------------------------
This relationship links the principles of electromagnetism directly to Newtonian mechanics. The interplay between these forces underpins the behaviour of charged particles in magnetic confinement devices and accelerators.
Once the magnetic force and centripetal force expressions are equated, the dependence of the radius on speed, charge, mass, and magnetic field strength becomes clear. This radius provides vital insight into how particles move in technological and natural contexts.
Radius of the Circular Path
By linking magnetic force to centripetal force, one obtains an expression for the radius of the particle’s path. Students must understand how the variables influence the orbit:
A greater velocity produces a larger radius.
A stronger magnetic field decreases the radius.
A larger mass increases the radius.
A larger charge decreases the radius.
These relationships demonstrate how the circular motion depends critically on particle properties and field strength, making it possible to identify species of charged particles based on their trajectories.
Motion of Positive and Negative Charges
The direction of circular motion depends on the sign of the charge. Because the magnetic force direction is determined by the particle’s charge and the directions of velocity and magnetic field, the following distinctions arise:
Positive charges curve in one direction.
Negative charges curve in the opposite direction.
This behaviour allows devices such as mass spectrometers to differentiate ions based on mass-to-charge ratio, using the curvature of the trajectory as a diagnostic tool.
Frequency and Period of Circular Motion
A charged particle in a uniform magnetic field completes each orbit in the same amount of time, regardless of radius or speed, provided the field remains constant. This leads to a characteristic frequency of rotation, often termed the cyclotron frequency, which is widely exploited in particle accelerators.
The constancy of the frequency highlights an important principle: although increasing the particle’s speed increases the radius, the time taken for a complete orbit is unaffected. This property enables precise acceleration and manipulation of particles in uniform magnetic fields.
Key Points for OCR Study
Students should be able to:
Recognise that magnetic force acts as a centripetal force for charged particles.
Describe why the motion is circular when velocity is perpendicular to the magnetic field.
Relate circular motion parameters to the variables B, Q, v, and m.
Use the relationships qualitatively to explain technological and physical phenomena.
Understand how the direction of curvature reveals the sign of the charge.
FAQ
The magnetic force is always perpendicular to the particle’s velocity, meaning it changes only the direction of motion, not the speed.
Because work is defined as force multiplied by displacement in the direction of the force, a perpendicular force does no work, so the kinetic energy stays constant.
Use the right-hand rule for the cross product v × B to determine the direction of the magnetic force on a positive charge.
For a negative charge, reverse the direction you obtain.
This enables prediction of clockwise or anticlockwise motion without resorting to left-hand or right-hand mnemonics.
Increasing speed increases the momentum term m v, which directly increases the radius r in the relationship r = m v / (B Q).
As a result, faster particles curve less sharply and take a wider circular path for the same field strength.
Possible causes include:
• Slight non-uniformities in the magnetic field.
• Collisions with residual gas molecules.
• Electric fields present due to charged surfaces or equipment.
• Gradual energy loss from radiation for very fast particles (synchrotron radiation).
Each factor disturbs the requirement of a constant perpendicular magnetic force.
The period of circular motion depends on mass, charge magnitude, field strength, and velocity component perpendicular to the field.
Since period depends on the magnitude of charge, not the sign, positive and negative particles with the same mass, speed, and field experience identical periods even though they rotate in opposite directions.
Practice Questions
A positively charged particle moves with a velocity that is perpendicular to a uniform magnetic field. Explain why the particle follows a circular path. (3 marks)
• Magnetic force acts perpendicular to velocity. (1)
• This force provides the centripetal force needed for circular motion. (1)
• Speed is unchanged because the magnetic force does no work. (1)
A particle with mass 3.2 × 10⁻²⁶ kg and charge +1.6 × 10⁻¹⁹ C enters a uniform magnetic field of flux density 0.45 T at a speed of 2.5 × 10⁵ m s⁻¹.
(a) State the expression for the magnetic force acting on the particle.
(b) Show how the radius of the particle’s circular path can be determined.
(c) Calculate the radius of the circular motion.
(d) Discuss how the radius would change if the particle had double the charge but the same speed and mass. (6 marks)
(a) States F = B Q v. (1)
(b) Recognises that magnetic force provides centripetal force: B Q v = m v² / r. (1)
(c) Rearranges to r = m v / (B Q) and substitutes correctly to obtain a value. Correct answer: approximately 0.11 m. (2)
(d) States that radius decreases if charge increases. (1)
• Correct reasoning: radius is inversely proportional to charge for constant m, v, and B. (1)

