OCR Specification focus:
‘Explain velocity selectors where electric and magnetic forces balance for selected speeds.’
Charged particles moving through crossed electric and magnetic fields experience competing forces that enable only particles with a specific velocity to pass through unchanged, forming a precise selection mechanism crucial in many physics applications.
Understanding Crossed Electric and Magnetic Fields
When a region contains an electric field and a magnetic field that are perpendicular both to each other and to the motion of a charged particle, the resulting situation is known as a crossed E and B field arrangement. This configuration is central to a device called the velocity selector, directly referenced in the OCR specification.
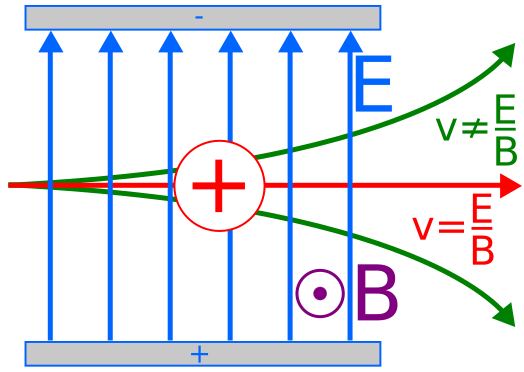
Diagram of a velocity selector showing a charged particle beam entering a region where electric and magnetic fields are perpendicular, allowing only particles with speed v = E/B to pass straight through while others are deflected. The image includes contextual mass-spectrometer elements that go beyond the syllabus requirement. Source.
A charged particle in such a setup encounters two fundamentally different forces acting simultaneously. Appreciating how these forces combine requires a clear understanding of the individual physical principles involved.
Electric Force on a Charged Particle
The electric field exerts a force on a charge according to the relationship F = EQ, acting in the direction of the field for a positive charge and opposite for a negative charge. This force is linear and independent of the particle’s velocity.
Electric Field Strength: The force per unit charge experienced by a small positive test charge placed in the field.
The electric field provides a constant directional influence, attempting to accelerate or decelerate any charged particle regardless of how fast it is moving.
A charged particle also experiences a magnetic force, which behaves quite differently.
Magnetic Force on a Moving Charge
The magnetic field exerts a force whose magnitude depends on the particle’s velocity, its charge, and the strength of the field.
EQUATION
—-----------------------------------------------------------------
Magnetic Force (F) = B Q v
B = Magnetic flux density, measured in tesla (T)
Q = Charge on the particle, measured in coulombs (C)
v = Velocity of the particle perpendicular to B, measured in metres per second (m s⁻¹)
—-----------------------------------------------------------------
Unlike the electric force, the magnetic force acts at right angles to both the velocity of the charge and the magnetic field direction, meaning the force does not change the particle’s speed—only its direction.
In crossed fields, these two forces act in opposite directions, leading to an important balance under the right conditions.
Velocity Selection: Balancing the Forces
A velocity selector is designed so that only charged particles travelling at a specific velocity experience equal electric and magnetic forces. When this equality occurs, the forces cancel and the particle continues along a straight path.
If the forces do not balance, the particle is deflected. The selector therefore acts as a filter, transmitting only particles at the chosen speed.
Deriving the Velocity Condition
Since the electric force is EQ and the magnetic force is BQv, balance is achieved when:
EQUATION
—-----------------------------------------------------------------
Velocity for Force Balance (v) = E / B
v = Speed of particle in m s⁻¹
E = Electric field strength in N C⁻¹
B = Magnetic flux density in T
—-----------------------------------------------------------------
This expression shows that the selector allows a very precise control over the velocity because both E and B can be tuned experimentally. A normal sentence must appear here to separate this equation from further structured content, ensuring clarity in the presentation.
Behaviour of Particles Within the Selector
To understand how the velocity selector works in practice, consider the following points:
If v < E/B, the magnetic force is too weak relative to the electric force, causing particles to be deflected toward the direction of the electric field.
If v > E/B, the magnetic force dominates, and particles are deflected toward the direction of the magnetic force.
If v = E/B, the forces cancel, and particles travel straight through the selector without deviation.
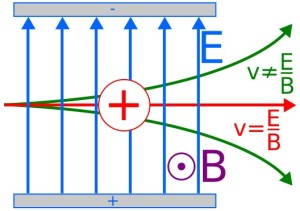
Simplified diagram of a velocity selector showing how the electric and magnetic forces act in opposite directions on a charged particle. Only particles with v = E/B travel straight through, while others curve away. The notation v ≠ E/B provides extra labels that reinforce the concepts already covered in the notes. Source.
This velocity-filtering behaviour is essential for producing beams of charged particles with uniform speeds.
Applications of Crossed E and B Fields
The OCR specification requires students to understand the function of a velocity selector, and recognising its real-world relevance strengthens comprehension. These fields underpin several advanced technologies where precise control over particle motion is crucial.
Mass Spectrometry
Velocity selectors help produce ion beams of uniform velocity before they enter magnetic deflection regions. This ensures mass-to-charge ratios are determined with high accuracy.
Cathode Ray and Particle Beam Devices
In older cathode ray technology and modern accelerator systems, crossed fields provide refined manipulation of electrons, maintaining beam coherence and allowing accurate targeting within instruments.
Plasma and Space Physics
Crossed-field behaviour governs many large-scale phenomena such as charged particle motion in planetary magnetospheres, helping explain radiation belts and auroral behaviour.
Key Points for OCR A-Level Students
Crossed electric and magnetic fields are perpendicular to one another and to particle motion.
The electric force acts linearly with charge and field strength.
The magnetic force depends on charge, speed, and magnetic flux density, acting perpendicular to motion.
A velocity selector transmits only particles travelling at speed v = E/B.
The selector operates by balancing electric and magnetic forces so particles travel straight through without deflection.
FAQ
The direction depends on which force dominates. The electric force acts along the electric field direction, while the magnetic force acts perpendicular to both velocity and magnetic field.
If the electric force is larger, the particle deflects towards the electric field. If the magnetic force dominates, the deflection follows the magnetic force direction.
Right-hand or left-hand rules can be used to determine the exact orientation for positively or negatively charged particles.
The magnetic force always acts perpendicular to the velocity of the particle. A force perpendicular to motion cannot do work because it does not contribute to movement in its own direction.
As a result, the speed of the particle remains constant, and only its direction can change.
This is why the magnetic force alone cannot accelerate or slow particles within a selector.
Several non-idealities affect accuracy:
• Edge effects at the ends of the plates can distort the electric field.
• Non-uniform magnetic fields may alter the balance condition.
• Variations in particle charge or initial velocity spread can reduce the sharpness of selection.
• Small misalignments between fields can introduce unwanted sideways forces.
These factors broaden the velocity range that passes through undeflected.
No. Neutral particles do not respond to electric or magnetic fields because they carry no net charge.
Since both forces in a velocity selector depend on charge, a neutral particle would pass straight through regardless of speed.
Specialised techniques such as time-of-flight methods must instead be used to analyse neutral beams.
Mass analysers rely on bending charged particles in a magnetic field so that their radius of curvature depends on mass-to-charge ratio.
If the particles enter with different speeds, their radii would differ even for the same mass, reducing the accuracy of measurements.
A velocity selector ensures all particles have the same speed, meaning that subsequent curvature depends only on mass-to-charge ratio, improving resolution.
Practice Questions
Question 1 (2 marks)
A charged particle enters a region containing perpendicular electric and magnetic fields. The electric field acts upwards and the magnetic field acts into the page.
State the condition required for the particle to pass straight through the region without deflection, and explain why this condition is necessary.
Mark scheme
States the condition v = E / B for undeflected motion. (1)
Explains that the electric and magnetic forces must be equal in magnitude and opposite in direction for the net force to be zero. (1)
Question 2 (5 marks)
A device uses crossed electric and magnetic fields to select charged particles of a particular speed.
Describe the roles of the electric and magnetic forces in such a velocity selector and explain how the device ensures that only particles with one specific speed emerge without deflection.
Include in your answer what happens to particles travelling faster or slower than the selected speed.
Mark scheme
States that the electric force acts on the charge in the direction of the electric field and is independent of speed. (1)
States that the magnetic force acts at right angles to both velocity and magnetic field and depends on particle speed. (1)
States that when v = E / B, the electric and magnetic forces balance, giving zero net force and straight-line motion. (1)
Describes that particles with v < E / B are deflected towards the electric field direction. (1)
Describes that particles with v > E / B are deflected in the direction of the magnetic force. (1)

