OCR Specification focus:
‘Use proton number Z, nucleon number A, and nuclide notation A_Z X for nuclei.’
Nuclear Notation and Numbers
This topic introduces the standard way physicists describe nuclei using symbols, numerical values, and structured notation. Understanding these conventions is essential for analysing nuclear processes, identifying isotopes, and interpreting nuclear equations.
The Role of Nuclear Notation
A nucleus is characterised by specific numbers that determine its identity and behaviour. Nuclear notation provides a concise, universally understood method of representing these quantities. It allows physicists to distinguish between different nuclides, track changes in nuclear reactions, and relate nuclear structure to physical properties such as stability.
Proton Number Z
The proton number, also called the atomic number, identifies the number of protons in a nucleus. It determines the chemical element because the number of protons governs the arrangement of electrons and hence chemical behaviour.
Proton Number (Z): The number of protons in the nucleus of an atom; it defines the element.
The proton number is always written as the lower left number in nuclear notation. It never changes during chemical processes but may change during certain nuclear transformations.
Nucleon Number A
The nucleon number gives the total number of nucleons—protons and neutrons—within the nucleus. It is sometimes referred to as the mass number, though mass is not exactly equal to A due to mass defect, a concept dealt with in another subtopic.
Nucleon Number (A): The total number of protons and neutrons in a nucleus.
Because it reflects the total nucleon count, A affects nuclear stability and helps differentiate between isotopes of the same element.
Nuclide Notation A₍Z₎X
Nuclear notation uses a structured symbol to represent nuclei clearly. The chemical symbol appears as X, with the nucleon number and proton number shown on the left-hand side.
Nuclide Notation (A_Z X): A standard representation of a nucleus using its chemical symbol X, nucleon number A as a superscript, and proton number Z as a subscript.
Between definition blocks and the normal text here, it is clear that nuclide notation supports precise communication, particularly when comparing isotopes or analysing nuclear equations.
Isotopes in Nuclear Notation
Isotopes are nuclei of the same element (same Z) but with different numbers of neutrons (different A).
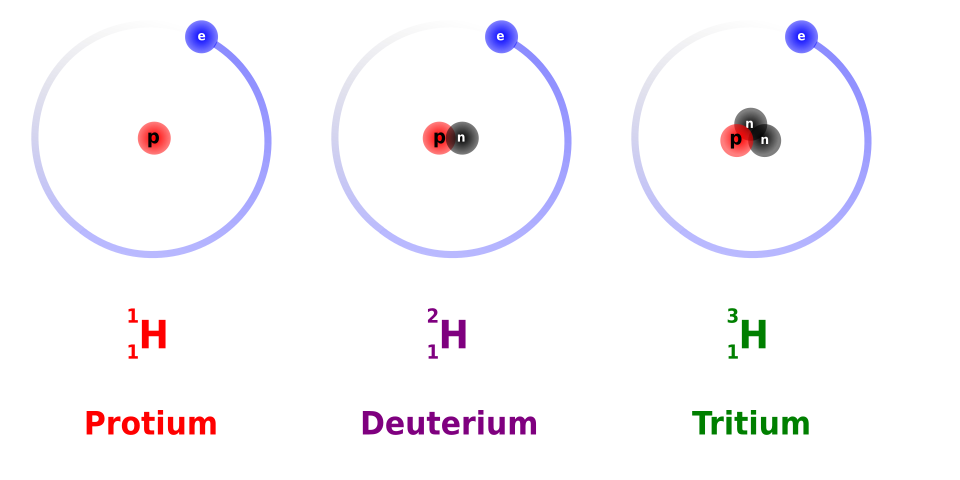
Diagram showing the three isotopes of hydrogen with their nuclei and electron orbits, labelled using nuclear notation (¹₁H, ²₁H, ³₁H). The diagram highlights that all isotopes share the same proton number Z = 1 but have different nucleon numbers A, reflecting different neutron numbers. The electron orbits are additional detail beyond the syllabus requirement, but they help reinforce that isotopes of the same element have identical electronic structure. Source.
Same X and Z
Different A
Neutron number N = A – Z
Isotopes often show similar chemical behaviour because electron structure depends on Z, but nuclear stability varies significantly because differences in neutron number alter nuclear binding.
Neutron Number and Its Significance
The neutron number is not shown directly in nuclear notation but can be calculated. It influences nuclear forces within the nucleus and affects the likelihood of certain types of radioactive decay.
Neutron Number (N): The number of neutrons in a nucleus, calculated using N = A – Z.
Nuclear notation therefore helps identify how neutron-rich or neutron-deficient a nucleus is, an important indicator of potential decay pathways.
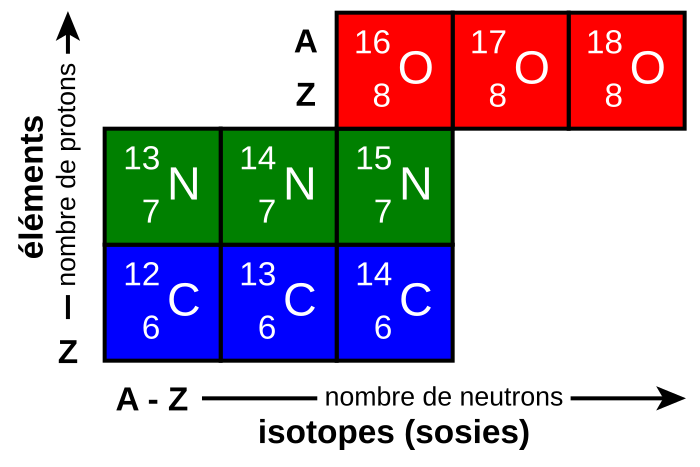
Diagram showing isotopes of carbon, nitrogen and oxygen arranged on axes of proton number Z and neutron number (A – Z), each box labelled with its nuclear notation A_Z X. The layout makes clear that changing A while keeping Z fixed produces isotopes of the same element with different neutron numbers. The French axis labels and the word “isotopes (sosies)” are additional language detail but do not introduce any extra physics beyond what is required for understanding nuclear notation and numbers. Source.
Why Nuclear Notation Matters
Nuclear notation is essential for picking apart nuclear reactions, ensuring that number conservation rules are followed. Nuclear equations must always balance both proton number and nucleon number.
Key uses include:
Tracking particles absorbed or emitted
Distinguishing between similar particles, including isotopes
Ensuring conservation of charge and nucleon number in nuclear equations
This system forms the foundation for understanding nuclear transformations encountered later in the course.
Charge and Mass Information in Notation
Although the notation primarily encodes nucleon structure, it implicitly provides charge data because proton number determines the nuclear charge. The total charge of the nucleus is +Ze, an important quantity when examining electric fields, scattering experiments or energy transitions.
Proton Number Z → charge +Ze
Nucleon Number A → relates to approximate nuclear mass
Chemical symbol X → fixed by Z
Thus, nuclear notation efficiently encapsulates several characteristics in a compact form.
Reading and Writing Nuclear Notation
To write nuclear notation systematically:
Place A as the superscript to the left of the chemical symbol.
Place Z as the subscript to the left of the chemical symbol.
Ensure that A ≥ Z, because neutrons cannot be negative.
For example:
Identifying isotope families
Analysing radioactive decay
Comparing nuclear properties across elements
This structured approach avoids ambiguity, especially when multiple nuclides of the same element are discussed.
Conservation in Nuclear Processes
Even though this section does not cover decay equations in detail, nuclear notation is indispensable for verifying conservation laws. Nuclear processes always conserve:
Proton number (charge conservation)
Nucleon number (mass number conservation)
Physicists apply nuclear notation to ensure these principles hold when interpreting or predicting nuclear reactions.
FAQ
The convention places the nucleon number A above the proton number Z to mirror how mass information is prioritised in nuclear physics. A is a quick indicator of the approximate nuclear mass, so placing it as the superscript makes it immediately visible.
Z, as the subscript, identifies the element and links directly to the periodic table. This layout keeps the most structurally defining quantity (A) visually dominant while still allowing Z to determine chemical identity.
Two nuclei are isotopes only if they share the same proton number Z, even if their chemical symbols appear different at first glance.
Check the following:
• Compare Z: if the proton numbers match, they are isotopes.
• Ensure the chemical symbols correspond to the same element.
• Differences in A will confirm variations in neutron number.
Neutron number N is derived directly from A and Z, so including it would make the notation unnecessarily cluttered.
N = A – Z is deliberately left as a calculated quantity because:
• It avoids repeating information already encoded.
• It prevents overly complex notation, especially for nuclides with long names.
• Nuclear reactions are more easily checked for conservation using A and Z alone.
Unstable isotopes often have neutron numbers significantly above or below the typical stable ratio for their proton number.
Using A and Z, physicists can:
• Calculate N and compare it with known stability ranges.
• Spot neutron-rich or neutron-deficient nuclides quickly.
• Identify isotopes likely to undergo beta decay due to an imbalance between protons and neutrons.
This makes nuclide notation a powerful tool in predicting nuclear behaviour.
Although notation for all elements uses the same A_Z X structure, nuclear stability depends strongly on how protons and neutrons interact.
Factors influencing the number of stable isotopes include:
• The strength of nuclear binding in mid-range elements.
• The increasing need for neutrons to offset proton–proton repulsion as Z becomes larger.
• Shell effects within the nucleus, which allow certain neutron numbers to be especially stable.
Thus, notation may look uniform, but nuclear forces determine how many A values correspond to stable forms.
Practice Questions
Question 1 (2 marks)
A nucleus of fluorine is represented by the notation 19_9F.
(a) State the proton number of this nucleus.
(b) State the number of neutrons in this nucleus.
Question 1 (2 marks)
(a) Proton number = 9
• 1 mark for stating 9
(b) Number of neutrons = 10
• 1 mark for correct subtraction: 19 – 9 = 10
Question 2 (5 marks)
The nuclide notation for an isotope of magnesium is 26_12Mg.
(a) Define the terms proton number and nucleon number.
(b) Determine the neutron number of this isotope.
(c) Explain how nuclide notation helps distinguish between different isotopes of the same element.
(d) A different isotope of magnesium has a nucleon number of 24. Explain what remains the same and what changes between this isotope and 26_12Mg, referring to nuclear structure.
Question 2 (5 marks)
(a) Definitions
• 1 mark: Proton number is the number of protons in the nucleus of an atom.
• 1 mark: Nucleon number is the total number of protons and neutrons in the nucleus.
(b) Neutron number
• 1 mark: Neutron number = 26 – 12 = 14
(c) Role of nuclide notation
• 1 mark: Explains that nuclide notation shows both proton number and nucleon number, allowing isotopes to be distinguished by differing nucleon (and therefore neutron) numbers.
(d) Comparison of isotopes
• 1 mark: States that the proton number (12) stays the same because both are magnesium.
• 1 mark: States that the nucleon number changes, so the number of neutrons changes between the isotopes.

