OCR Specification focus:
‘Use R = r₀ A^(1/3); discuss typical atomic and nuclear mean densities.’
Nuclear radii and densities reveal how matter is structured at its smallest scales, showing remarkably compact nuclei within relatively vast atoms and highlighting the immense density of nuclear material.
Nuclear Size and Scaling Relationships
Understanding nuclear radius is central to building a simple quantitative model of nuclear structure. Nuclei vary in size depending on the number of nucleons they contain, yet their radii follow a predictable pattern across all isotopes. This regularity allows nuclear physicists to estimate the spatial extent of different nuclei and compare them with the much larger dimensions of whole atoms. Such comparisons reinforce one of the key ideas in nuclear physics: although the nucleus contains nearly all of an atom’s mass, it occupies only a minute fraction of the total atomic volume.
When discussing nuclear size, it is essential to introduce the empirical nuclear radius relationship, expressed using mass number and a proportionality constant. This formula reflects the approximately constant density of all nuclei, implying that as the number of nucleons increases, radius grows only slowly and the nuclear material remains extremely compact.
EQUATION
—-----------------------------------------------------------------
Nuclear Radius (R) = r₀ A^(1/3)
R = Nuclear radius (metres)
r₀ = Nuclear radius constant, typically about 1.2–1.5 fm
A = Nucleon number (dimensionless)
—-----------------------------------------------------------------
This relationship shows that nuclear radius scales with the cube root of nucleon number, so doubling the mass number does not double the radius; instead, it increases only modestly.
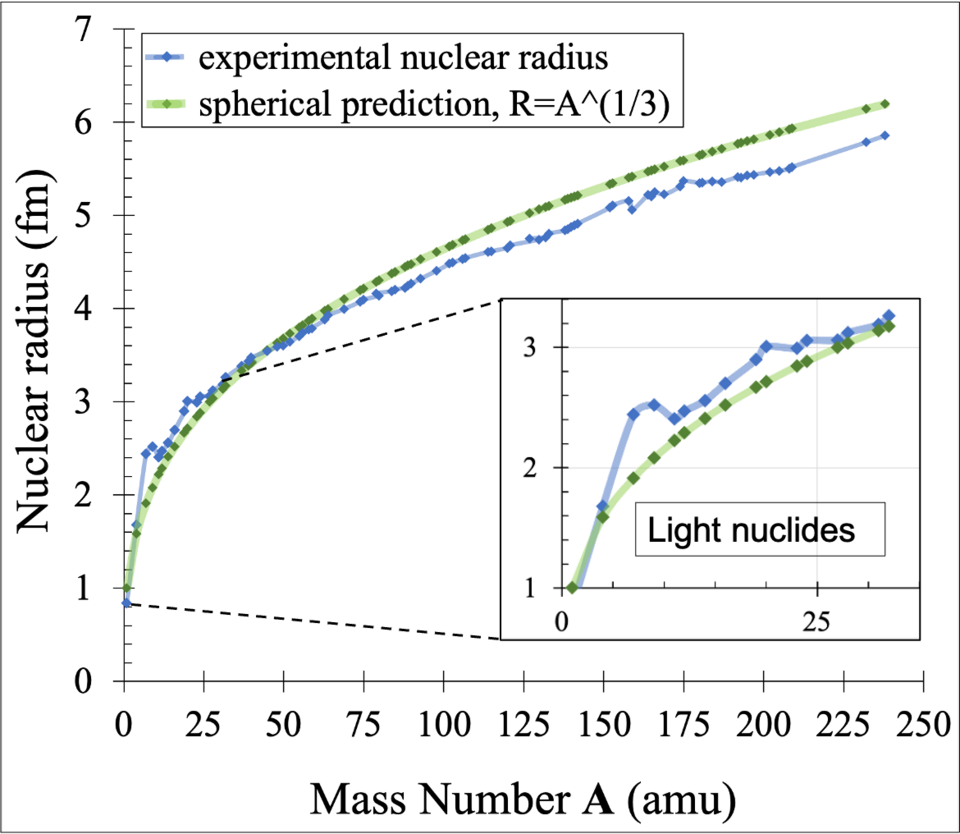
Graph showing experimental nuclear radii and the theoretical R ∝ A¹ᐟ³ relationship, illustrating the slow increase of radius with increasing nucleon number and the approximated constant nuclear density across nuclei. Source.
Typical Nuclear Radii
Measurements from high-energy scattering experiments and other probes reveal that most nuclei fall within a narrow range of radii. While lighter nuclei may have radii close to 2–3 femtometres, heavier nuclei extend to around 7–8 femtometres. These sizes are extraordinarily small compared with atomic radii, which are typically around 0.1 nanometres (10⁵ femtometres).
To help students appreciate this distinction, it is useful to emphasise the enormous emptiness of the atom: electrons orbit at distances tens of thousands of times larger than the nuclear radius.
Despite occupying such a tiny region of space, the nucleus contains nearly all the atom’s mass.
Key features of nuclear radius behaviour
Nuclear radius grows slowly with increasing nucleon number.
The parameter r₀ acts as a universal constant for stable nuclei.
Nuclear radii are on the order of 1–10 femtometres, far smaller than typical atomic scales.
The cubic-root relationship implies a roughly constant nuclear density across different elements.
Nuclear Density: A Remarkably High Value
The concept of nuclear density helps quantify the compactness of nuclear matter. Density depends on mass and volume, and because nuclear mass is concentrated in an extremely small radius, nuclear material has one of the highest known densities in nature. Unlike atomic density, which varies between elements depending on electron arrangements and bonding, nuclear density is essentially constant because nucleons are packed with similar spacing in all nuclei.
Nuclear Density: The mean mass per unit volume of nuclear material, assumed roughly constant for all nuclei owing to the uniform distribution of nucleons.
Because nuclear radius increases only as A^(1/3), while mass increases proportionally to A, the ratio of mass to volume remains constant. This leads to typical nuclear densities of around 2–3 × 10¹⁷ kg m⁻³, a value far greater than any everyday material density.
Nuclear density is not only a theoretical construct but also a physical parameter with wide scientific relevance. It underpins our understanding of extreme astrophysical bodies, such as neutron stars, which contain matter compressed to nuclear densities. Although not part of this syllabus point, noting this connection illustrates to students why learning about nuclear size and density is meaningful beyond the laboratory.
Features of nuclear density
Nuclear density is essentially constant across all stable nuclei.
It is determined by the A^(1/3) scaling of nuclear radius.
Values exceed typical atomic or material densities by many orders of magnitude.
High nuclear density reflects the powerful binding effects of the strong nuclear force.
A schematic depiction of a helium nucleus, showing tightly packed protons and neutrons. Its compact structure illustrates the extremely high density of nuclear matter. The example is isotope-specific but representative of nucleon packing in all nuclei. Source.
Comparing Atomic and Nuclear Scales
The OCR specification emphasises discussion of typical atomic and nuclear mean densities, and this contrast is crucial for conceptual understanding. Atoms consist mostly of empty space, giving them extremely low mean density compared with their nuclei.
Key contrasts include:
Atomic radius ≈ 10⁵ times greater than nuclear radius.
Nucleus contains almost all atomic mass, yet occupies an incredibly small volume.
Mean atomic density is therefore far lower than nuclear density.
The spatial emptiness of the atom explains why materials can be compressed and why scattering experiments reveal little obstruction unless probing very near the nucleus.
Together, the nuclear radius relationship and the concept of nuclear density provide students with a coherent picture of the minuscule yet massively compact nature of nuclei, forming a foundation for deeper exploration of nuclear structure and interactions.
FAQ
The value of r0 is obtained by analysing scattering data from high-energy particle experiments. Alpha particles, electrons, or protons are fired at thin targets, and their deflection patterns reveal how close they approach the nuclear surface.
A best-fit curve is then applied to measurements of nuclear radii across many different nuclei.
• Electron scattering is particularly useful because electrons experience negligible strong-force effects.
• The resulting data consistently support a value of r0 between 1.2 and 1.5 femtometres.
The cubic-root law is an approximation. Real nuclei vary slightly due to differences in shape and internal structure.
Deviations occur because:
• light nuclei are less uniform and may not be perfectly spherical
• some heavy nuclei exhibit deformation, becoming slightly elongated
• shell effects can alter how nucleons are distributed
Despite these variations, the cubic-root dependence holds well enough for most calculations at A-Level.
The spherical model simplifies the mathematics and works well because, on average, nucleons distribute themselves symmetrically due to the strong nuclear force.
In reality, some nuclei display deformation, especially those with large nucleon numbers or particular proton–neutron configurations. However, these departures from sphericity are small enough that a spherical approximation provides reliable estimates of volume and density for most purposes.
Nuclear density is typically described as constant because the central region of a nucleus is very uniform. However, the actual local distribution is more nuanced.
• The density is highest at the core, with only a slight decrease moving outward.
• At the surface, density falls rapidly over a distance of around 2 femtometres.
• This transition region is called the nuclear surface or "skin."
Thus the quoted density is an average rather than a point-by-point measurement.
Nuclear density, around 2–3 × 10^17 kg m^-3, is extraordinarily high and is matched only in extreme cosmic environments.
• Neutron stars contain matter compressed to near-nuclear densities, with only a thin crust of lower-density material.
• Their structure provides insight into how nucleons behave under immense pressure, far beyond what can be reproduced experimentally.
Although not part of the A-Level specification, this parallel helps contextualise why modelling nuclear density is scientifically important.
Practice Questions
Question 1 (2 marks)
State the relationship between nuclear radius and nucleon number, and explain what this implies about nuclear density across different nuclei.
Question 1 (2 marks)
• States the relationship R = r0 A^(1/3). (1 mark)
• Explains that because radius increases with the cube root of A, nuclear density remains approximately constant for all nuclei. (1 mark)
Question 2 (5 marks)
A student claims that because heavier nuclei contain many more nucleons, they must have much higher densities than lighter nuclei.
Using the nuclear radius equation R = r0 A^(1/3), explain why this claim is incorrect.
In your answer, refer to:
• how nuclear radius changes with nucleon number
• how nuclear volume depends on radius
• how this leads to an approximately constant nuclear density for all nuclei
• the implications this has for comparing atomic and nuclear scales.
Question 2 (5 marks)
• States or uses the relationship R ∝ A^(1/3). (1 mark)
• States that volume is proportional to R^3. (1 mark)
• Recognises that because R^3 ∝ A, nuclear volume increases proportionally to nucleon number. (1 mark)
• Concludes that density (mass/volume) is therefore roughly constant for all nuclei. (1 mark)
• Mentions an implication such as: nuclei remain extremely dense compared with atoms; atomic radius is vastly larger than nuclear radius; most atomic volume is empty space. (1 mark)

