OCR Specification focus:
‘Distinguish scalar and vector quantities and provide appropriate examples of each.’
In physics, quantities are used to describe and measure the physical world. Understanding the distinction between scalars and vectors is essential, as it defines how quantities interact and combine in physical processes. Scalars involve only magnitude, while vectors combine magnitude and direction, enabling complete physical descriptions of motion, force, and other vector phenomena.
Scalars and Vectors: The Basis of Quantities
Physical quantities can be categorised according to whether they possess direction as well as magnitude. This categorisation influences how quantities are measured, added, or used in equations that describe natural phenomena.
Scalar Quantities
Scalar Quantity: A physical quantity that has magnitude only and no direction.
Scalar quantities are fully described by a single numerical value with an associated unit. They are used where direction does not affect the physical meaning of the quantity.
Common examples of scalar quantities include:
Mass (kg) – the amount of matter in an object.
Temperature (K or °C) – a measure of the average kinetic energy of particles.
Time (s) – a measure of duration.
Energy (J) – the capacity to do work.
Speed (m s⁻¹) – the rate of change of distance.
Distance (m) – the total path length travelled.
These quantities can be added, subtracted, or compared using ordinary arithmetic since they have no directional component. For instance, total energy can be calculated simply by summing scalar energy values.
Scalar quantities obey the rules of algebra and are unaffected by orientation in space. They are measured with instruments that do not need alignment or directional reference, such as thermometers or balances.
Vector Quantities
Vector Quantity: A physical quantity that has both magnitude and direction.
A vector is represented by an arrow, where the length corresponds to its magnitude and the arrowhead indicates its direction. Vectors are essential for describing phenomena involving direction-dependent behaviour.
Examples of vector quantities include:
Displacement (m) – the straight-line distance and direction from one point to another.
Velocity (m s⁻¹) – the rate of change of displacement.
Acceleration (m s⁻²) – the rate of change of velocity.
Force (N) – a push or pull acting in a specific direction.
Momentum (kg m s⁻¹) – the product of mass and velocity, showing motion direction and magnitude.
Electric field strength (N C⁻¹) – the force per unit charge, acting in a defined direction.
When dealing with vectors, both magnitude and direction must be considered. Two vectors of equal magnitude but opposite directions are not identical—they cancel if added together.
Representing Vectors
Vectors are drawn using a scale diagram or expressed using component notation, such as Fx and Fy, representing the projections of a vector along perpendicular axes. The direction of a vector can also be expressed using angles or compass bearings.
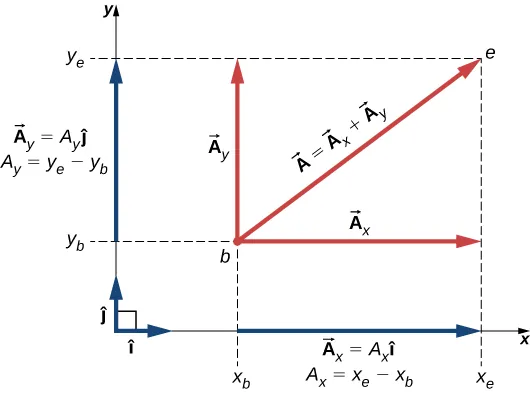
A vector A drawn in Cartesian coordinates, with perpendicular components Aₓ and Aᵧ. The components show how a vector’s direction and magnitude are resolved along two axes. Source.
Vectors may be described in three main ways:
Graphically, by arrows in diagrams.
Algebraically, by components (e.g. using trigonometric relationships).
Symbolically, with bold type (e.g. F) or a vector arrow (→) above the letter.
Vector representation is essential for calculating resultant forces, displacements, and other derived quantities in mechanics and fields.
Distinguishing Scalars from Vectors
Scalars and vectors can often describe related but distinct aspects of the same physical situation. For example:
Speed is the scalar magnitude of velocity.
Distance is the scalar equivalent of displacement.
Work (a scalar) is calculated using the dot product of force (vector) and displacement (vector).
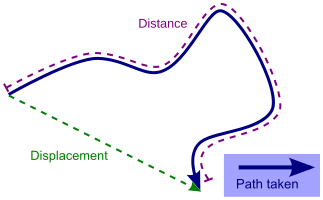
A simplified diagram comparing distance and displacement. Distance measures the total path length, while displacement is a vector showing direction and magnitude between start and end points. Source.
Understanding which quantities are scalar or vector prevents conceptual errors and ensures correct application of physical laws.
Key Differences
Magnitude: Scalars have only magnitude; vectors have both magnitude and direction.
Representation: Scalars are represented by simple numbers; vectors by arrows or bold letters.
Combination Rules: Scalars combine using normal arithmetic; vectors require vector addition rules.
Effect of Direction: Direction affects vectors but not scalars.
Transformation: Vectors change when the coordinate system is rotated; scalars remain invariant.
Vector Notation and Conventions
Vector quantities are typically denoted in bold or with an arrow symbol, such as F or 𝐹⃗, whereas scalar quantities use standard italic text, such as m or E.
The magnitude (size) of a vector A is written as |A| or simply A when context makes the distinction clear.
Directional Representation
The direction of a vector is commonly described:
Using angles relative to a reference axis (e.g. 30° above the horizontal).
By cardinal directions (north, south, east, west).
In component form, as Aₓ and Aᵧ, representing horizontal and vertical parts respectively.
A clear and consistent notation ensures accurate communication and calculation of physical relationships.
Combining Scalar and Vector Quantities
When combining quantities, it is essential to apply correct rules:
Scalars can be added or subtracted directly (e.g. total energy).
Vectors must be combined using vector addition, taking account of both direction and magnitude.
Example Contexts
Adding forces acting at angles involves vector addition to find the resultant force.
Summing displacements along different paths requires direction-aware addition to obtain net displacement.
Kinetic energy, although related to the vector quantity velocity, remains a scalar because it depends on the square of magnitude only.
This distinction between scalar and vector combination underpins many key analytical methods in mechanics and fields.
Applications of Scalars and Vectors
Understanding scalars and vectors provides the foundation for analysing physical interactions:
In mechanics, vectors describe motion, forces, and momentum.
In electric and magnetic fields, vectors define the strength and direction of fields.
In thermodynamics, scalar quantities like temperature and energy describe systems without directional dependence.
Accurate recognition and manipulation of scalar and vector quantities are fundamental to all branches of physics, enabling consistent analysis, prediction, and explanation of real-world phenomena.
FAQ
Consider whether the quantity requires a direction to be fully described. If the quantity changes depending on direction or can be represented by an arrow, it is a vector.
If it remains the same regardless of direction, it is a scalar. For instance, pressure is scalar because it acts equally in all directions, while force is vector because it acts in a particular direction.
Temperature is a measure of average kinetic energy, which has no inherent direction. It represents a state at a point rather than a directional change.
Heat flow, on the other hand, is a vector process because it occurs from higher to lower temperature regions — the flow has a defined direction, but the temperature itself does not.
Yes. A zero vector can exist when the magnitude is zero but the concept of direction remains defined mathematically.
For example:
If two equal and opposite forces act on an object, their resultant force is a zero vector.
The zero vector represents equilibrium — no net effect, but it is still treated as a vector quantity in equations.
Scalars lack direction, so they can only be added or subtracted based on magnitude. Cancellation occurs only when opposing directions exist, which scalars do not have.
For example, 10 J of energy added and 10 J removed results in zero energy change, but this is arithmetic subtraction, not vector cancellation. Vectors can cancel due to opposing directions even when their magnitudes are non-zero.
Breaking vectors into components simplifies analysis, particularly when multiple vectors act at angles.
Advantages include:
Each component (x and y) can be treated as an independent scalar quantity.
Vector addition and subtraction become simpler — add x-components and y-components separately.
It allows straightforward calculation of resultants using Pythagoras’ theorem and trigonometric functions.
This method is widely used in mechanics, projectile motion, and force analysis to avoid unnecessary geometric constructions.
Practice Questions
Question 1 (2 marks)
State the difference between a scalar quantity and a vector quantity. Give one example of each.
Mark Scheme:
1 mark for stating that a scalar has magnitude only, whereas a vector has both magnitude and direction.
1 mark for providing one correct example of each (e.g. scalar: time, mass, or energy; vector: velocity, force, or displacement).
Question 2 (5 marks)
A student walks 40 m east, then 30 m north.
(a) Calculate the magnitude of the student’s resultant displacement. (3 marks)
(b) State the direction of the resultant displacement relative to the east direction. (2 marks)
Mark Scheme:
(a)
1 mark for correctly applying Pythagoras’ theorem:
resultant displacement = √(40² + 30²)1 mark for obtaining the correct numerical result: 50 m
1 mark for including a suitable unit (metres or m)
(b)
1 mark for using trigonometry to find the angle:
θ = tan⁻¹(30/40)1 mark for giving the correct direction: approximately 37° north of east (accept 36.9°, 37°, or “north-east direction”).

