OCR Specification focus:
‘Add and subtract vector quantities using appropriate methods and notation.’
Understanding how to add and subtract vectors is essential in A-Level Physics, as it enables analysis of forces, motion, and fields acting in various directions with precision and clarity.
Vector Addition and Subtraction
The Nature of Vectors
A vector quantity possesses both magnitude (size) and direction. Common examples include displacement, velocity, acceleration, and force.
Vector: A quantity with both magnitude and direction, represented by an arrow whose length denotes magnitude and whose orientation indicates direction.
Vectors are typically drawn as arrows on diagrams. The tail of the arrow marks the starting point, and the head indicates the direction of action. This representation allows for visual and analytical methods of combining multiple vectors.
Methods of Vector Addition
1. The Head-to-Tail Method
The head-to-tail method is the most common graphical technique for vector addition.
Begin by drawing the first vector to scale in the correct direction.
Position the tail of the second vector at the head of the first.
The resultant vector is drawn from the tail of the first vector to the head of the second.
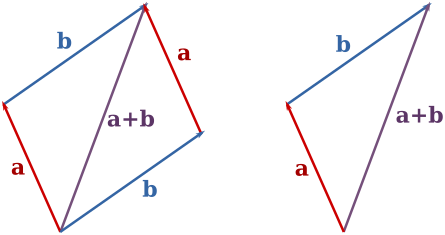
Two equivalent graphical constructions for vector addition. Both form a triangle from A and B, highlighting that the order of head-to-tail placement does not change the resultant. The simple arrows and labels keep the focus on magnitude and direction only. Source.
This method demonstrates how two or more vectors combine to produce a single equivalent vector, known as the resultant.
Resultant Vector: The single vector that has the same effect as two or more vectors acting together.
The magnitude of the resultant can be measured directly from the scale diagram, while the direction is found using a protractor. This visual technique provides a clear, intuitive understanding of vector combination.
2. The Parallelogram Method
The parallelogram method is another graphical approach, especially useful when the vectors share a common starting point.
Draw both vectors from the same origin.
Complete a parallelogram by drawing lines parallel to each vector.
The diagonal of the parallelogram from the common origin represents the resultant vector.
This method reinforces the geometric nature of vector addition and is particularly useful when working with forces or displacements acting from a single point.
3. Analytical Vector Addition
When vectors are not conveniently aligned, analytical methods using trigonometry or components provide precise results.
If two vectors A and B make an angle θ between them, the magnitude of the resultant R can be calculated using the cosine rule.
EQUATION
—-----------------------------------------------------------------
Resultant of Two Vectors (R) = √(A² + B² + 2AB cosθ)
R = Magnitude of the resultant vector (unit depends on quantity, e.g. N or m s⁻¹)
A, B = Magnitudes of the individual vectors (same unit as R)
θ = Angle between the two vectors (degrees or radians)
—-----------------------------------------------------------------
The direction of the resultant relative to one of the vectors can be found using the sine rule or trigonometric ratios.
These analytical methods are especially important in physics problems involving forces at angles or projectile motion.
Vector Subtraction
Understanding Subtraction
Vector subtraction involves finding the difference between two vectors — effectively determining what must be added to one vector to reach another.
To subtract vector B from vector A, we reverse the direction of B to form –B, then add A and –B using the head-to-tail or analytical method.
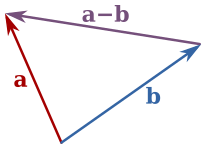
Vector subtraction illustrated as A + (−B). The diagram emphasises that −B has the same magnitude as B but the opposite direction, so the head-to-tail sum gives A − B. This mirrors the construction described in the text. Source.
Draw vector A.
Reverse vector B to form –B (same magnitude, opposite direction).
Use head-to-tail addition of A + (–B).
The resultant gives A – B.
This process is equivalent to adding the negative of a vector and forms the foundation of understanding relative motion and equilibrium conditions in physics.
Subtraction in Component Form
In analytical work, vectors can be represented by their components along perpendicular axes. This allows for straightforward addition or subtraction by combining corresponding components.
EQUATION
—-----------------------------------------------------------------
Resultant Components
Rx = Ax ± Bx
Ry = Ay ± By
R = √(Rx² + Ry²)
θ = tan⁻¹(Ry / Rx)
Rx, Ry = Resultant components in x and y directions (units depend on context)
Ax, Ay = Components of vector A
Bx, By = Components of vector B
θ = Angle of resultant relative to x-axis
—-----------------------------------------------------------------
Adding or subtracting components ensures vectors are treated consistently according to their directions. For subtraction, simply use the negative of the corresponding component.
Notation and Representation
Vector Symbols
Vectors are often denoted by bold letters (e.g., F, v) or by an arrow above the symbol (→), such as F⃗. Scalar quantities, by contrast, use ordinary italic letters.
Direction and Angles
When representing vectors, it is vital to include directional information, typically in degrees from a defined axis (e.g., 30° above the horizontal). The sense of direction must always be made clear.
The Importance of Scale and Units
All vectors on diagrams should:
Be drawn to scale when practical.
Include a scale statement (e.g., 1 cm = 5 N).
Show units consistently across all components and results.
Clarity in notation avoids confusion, especially when multiple vectors act simultaneously.
Applications of Vector Addition and Subtraction
Vector addition and subtraction underpin a wide range of physical phenomena:
Forces combining to produce a net force on an object.
Velocities of moving objects relative to each other (e.g. aircraft in wind).
Displacements in different directions leading to a resultant path.
In all these cases, the fundamental rule remains: vectors must be combined using both magnitude and direction, respecting their true physical nature.
Equilibrium and Resultant Conditions
When two or more forces act on a body and the resultant is zero, the object is said to be in equilibrium. This means the vector sum of all forces equals zero.
Equilibrium: The state in which the sum of all forces (and moments, if considered) acting on a body equals zero, resulting in no acceleration.
Recognising this vector balance is vital in mechanics, statics, and motion analysis, where correct vector addition and subtraction ensure accurate predictions of physical behaviour.
FAQ
If vectors are not drawn to scale, the resulting diagram will not accurately represent the magnitudes or directions of the quantities involved. This can lead to incorrect conclusions about the size or direction of the resultant vector.
To ensure precision:
Always include a clear scale, such as “1 cm = 2 N.”
Use a ruler and protractor to maintain consistent measurements.
Label vectors clearly with their magnitudes and directions.
Graphical accuracy is vital for reliable physical interpretation, especially when estimating resultant forces or displacements.
Scalar addition involves quantities with only magnitude, so they can be added algebraically without considering direction (e.g., mass or energy).
Vector addition, however, must consider both magnitude and direction. Two vectors may cancel out or reinforce each other depending on their relative orientation.
For example:
Two 5 N forces acting in the same direction give a resultant of 10 N.
Two 5 N forces acting in opposite directions give a resultant of 0 N.
Direction is therefore crucial in all vector operations.
The head-to-tail method is the most intuitive and least error-prone way to visualise vector addition. It demonstrates clearly how vectors combine sequentially to produce a single resultant.
It is preferred because:
It visually mirrors how displacements or forces act in sequence.
It can be easily extended to three or more vectors.
The resultant’s direction and magnitude are immediately measurable.
This makes it ideal for experimental or diagram-based analysis where precise scale drawings are required.
Yes. If the reversed vector (–B) points roughly in the same direction as the original vector A, subtracting B (i.e., A – B) effectively becomes similar to adding two vectors that reinforce each other.
For example:
If A = 5 N east and B = 3 N west, then A – B = 8 N east.
The reversal of B makes the vectors align, increasing the resultant magnitude.
This highlights that vector subtraction depends entirely on the relative directions, not just magnitudes.
Each vector can be resolved into perpendicular x and y components. These components can then be added or subtracted separately to find the overall resultant.
Steps:
Resolve each vector into components using trigonometric functions (cosθ and sinθ).
Add or subtract the x-components and y-components independently.
Recombine using Pythagoras’ theorem to find the resultant magnitude and direction.
This component method is especially useful for analytical work and avoids the measurement inaccuracies of scale drawings.
Practice Questions
Question 1 (2 marks)
Two forces, 6 N and 8 N, act on an object at right angles to each other.
(a) State the name given to the single force that has the same effect as these two forces. (1 mark)
(b) Determine the magnitude of this single force. (1 mark)
Mark scheme for Question 1
(a) Resultant force – 1 mark
(b) Correct use of Pythagoras’ theorem: √(6² + 8²) = 10 N – 1 mark
Question 2 (5 marks)
A boat travels across a river. It has a velocity of 3.0 m s⁻¹ due north relative to the water. The river current flows east at 2.0 m s⁻¹ relative to the bank.
(a) Represent these two velocity vectors using a scale diagram or by calculation. (1 mark)
(b) Determine the boat’s resultant velocity relative to the riverbank. (2 marks)
(c) Calculate the direction of motion of the boat relative to north. (2 marks)
Mark scheme for Question 2
(a) Diagram or correct description showing two perpendicular velocity vectors: one 3.0 m s⁻¹ north, one 2.0 m s⁻¹ east – 1 mark
(b) Correct use of Pythagoras’ theorem: resultant = √(3.0² + 2.0²) = 3.6 m s⁻¹ – 1 mark
Clear statement that resultant velocity is 3.6 m s⁻¹ relative to the riverbank – 1 mark
(c) Use of tanθ = 2.0 / 3.0 – 1 mark
Correct calculation of θ = 33.7° (or 34°) east of north – 1 mark

