In physics, resolving vectors into components allows complex forces or motions to be analysed in simpler perpendicular directions, simplifying problem-solving and linking vector quantities to measurable effects.

Understanding Vector Resolution

A vector is a quantity that has both magnitude and direction. Examples include displacement, velocity, acceleration, and force. When vectors act in directions that are not aligned with the coordinate axes, they can be resolved into components that act along perpendicular directions—typically the x-axis (horizontal) and y-axis (vertical).

Resolving a vector enables analysis of how much of its effect acts along each direction, making it easier to apply Newton’s laws, conservation principles, or motion equations in one dimension at a time.

The Principle of Perpendicular Components

Every vector in a plane can be represented as the sum of two perpendicular components. If a vector ( F ) acts at an angle θ to the horizontal, its perpendicular components can be expressed mathematically as:

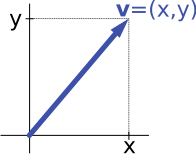
A single vector is decomposed into orthogonal horizontal (x) and vertical (y) components. This makes analysis along each axis independent and directly supports using Fx = F cos θ and Fy = F sin θ. Labels are minimal to emphasise the component idea only. Source.

EQUATION
—-----------------------------------------------------------------
Vector Components
Fx = F cosθ
Fy = F sinθ
Fx = Horizontal component of the vector F, measured in newtons (N)
Fy = Vertical component of the vector F, measured in newtons (N)
F = Magnitude of the original vector, measured in newtons (N)
θ = Angle between F and the horizontal, measured in degrees or radians
—-----------------------------------------------------------------

These expressions result from trigonometric relationships within a right-angled triangle formed by the vector and its components.

Geometrical Representation

Visualising Vector Components

A vector can be represented as the diagonal of a rectangle, with its horizontal and vertical sides corresponding to the perpendicular components. When resolving a vector graphically:

• Draw the vector to scale in its correct direction.

• From the head (or tail) of the vector, draw perpendicular lines to form a right-angled triangle.

• The lengths of the sides along the axes represent Fx and Fy.

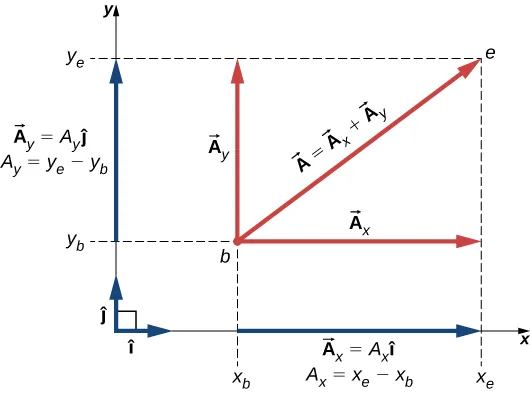
The vector is the diagonal; its x- and y-components are perpendicular projections onto the axes. Unit vectors î and ĵ define axis directions, enabling the compact representation F = Fx î + Fy ĵ. This directly supports resolving into components before recombining vectorially. Source.

This geometric interpretation shows that the vector sum of Fx and Fy reproduces the original vector both in magnitude and direction.

Mathematical Basis of Resolution

Trigonometric Relationships

Resolution uses basic trigonometry applied to the right-angled triangle formed by the vector and its components:

• The adjacent side corresponds to Fx = F cosθ.

• The opposite side corresponds to Fy = F sinθ.

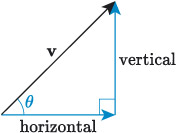
A vector v makes an angle θ with the horizontal; the adjacent side is the x-component and the opposite side is the y-component. Using right-triangle trigonometry gives vx = |v| cos θ and vy = |v| sin θ. The diagram focuses tightly on these component relationships. Source.

EQUATION
—-----------------------------------------------------------------
Resultant Vector Magnitude
F = √(Fx² + Fy²)
F = Magnitude of the vector (N)
Fx = Horizontal component (N)
Fy = Vertical component (N)
—-----------------------------------------------------------------

This relationship confirms that combining the two perpendicular components restores the original vector — demonstrating that vector resolution and vector addition are inverse processes.

Importance of Coordinate Axes

To resolve vectors accurately, one must establish clear coordinate axes. The most common convention in physics problems is:

• x-axis: Horizontal direction.

• y-axis: Vertical direction.

However, in inclined-plane problems or non-orthogonal systems, axes may be chosen to simplify analysis (for example, one axis parallel to a slope). Regardless of orientation, the principle remains that components must be perpendicular.

Choosing axes aligned with physical features of a problem often reduces complexity, as one component may correspond to a known quantity or be zero.

Physical Applications

Resolving vectors into components is fundamental in many areas of physics, including:

• Forces: Determining how a single force contributes to motion in different directions.

• Projectile motion: Separating horizontal (constant velocity) and vertical (accelerated) motion.

• Equilibrium problems: Ensuring the sum of forces in each perpendicular direction equals zero.

• Circular motion and fields: Analysing centripetal and tangential components of velocity or field strength.

By resolving vectors, physical problems can be broken into simpler one-dimensional forms, each analysed independently before recombining results.

Analytical and Graphical Resolution

Analytical Method

This approach uses trigonometric equations to calculate component magnitudes:

1. Identify the magnitude of the vector and the angle θ it makes with a reference axis.

2. Apply Fx = F cosθ and Fy = F sinθ.

3. Assign appropriate signs (+ or –) depending on direction relative to chosen axes.

This method is especially efficient when the vector magnitude and direction are known precisely.

Graphical Method

This involves drawing the vector to scale and constructing perpendicular projections to measure component magnitudes. Although less precise than analytical methods, it is valuable for visualising relationships between vectors, particularly in qualitative analysis or experimental setups.

Directional Considerations and Sign Convention

The sign of each component depends on its orientation:

• Components acting along the positive axis are positive.

• Components acting against the axis direction are negative.

Correctly assigning signs ensures accurate application of Newton’s laws and equilibrium conditions.

Sign convention is crucial when summing multiple vectors or calculating resultant forces, as incorrect signs can lead to significant conceptual and numerical errors.

Conceptual Links to Vector Addition

Vector resolution is directly linked to vector addition. The two perpendicular components combine vectorially to reproduce the original vector. In mathematical terms, the vector F can be expressed as:

EQUATION
—-----------------------------------------------------------------
Vector Representation
F = Fx î + Fy ĵ
F = Resultant vector
Fx = Horizontal component (N)
Fy = Vertical component (N)
î, ĵ = Unit vectors along x and y axes respectively
—-----------------------------------------------------------------

This vector form is central in analytical physics, allowing motion and forces to be described in compact coordinate notation, which is especially useful in two-dimensional and three-dimensional problems.

Practical Context in Experiments

In laboratory work, resolving vectors helps interpret measurements such as forces on an inclined plane or current in perpendicular conductors. For instance:

• A force sensor may measure total force, while components determine acceleration along or perpendicular to motion.

• Error analysis in measurements may depend on directional components if sensors are aligned with particular axes.

Understanding and applying vector resolution ensures that theoretical equations correspond accurately to practical measurement setups, fulfilling a key aim of the OCR A-Level Physics curriculum.