OCR Specification focus:
‘Solve trajectory, range, and time-of-flight problems using component vectors and kinematic equations.’
Projectile motion combines horizontal constant velocity and vertical constant acceleration to describe an object’s curved path. Analysing trajectories uses vector components and kinematic equations.
Analysing Projectile Trajectories
A projectile is any object launched into the air and moving under the influence of gravity alone, with air resistance neglected. Its motion can be separated into independent horizontal and vertical components, allowing two-dimensional motion to be studied using one-dimensional equations applied in each direction.
The trajectory of a projectile is the curved path it follows — a parabola when gravity is uniform and no resistive forces act.
Key Concepts in Trajectory Analysis
Projectile motion assumes:
Constant acceleration vertically (due to g, the acceleration of free fall)
Constant velocity horizontally (no horizontal forces)
A single launch point and landing plane, unless otherwise stated
Negligible air resistance
By resolving the initial velocity vector into two perpendicular components, the motion can be studied separately:
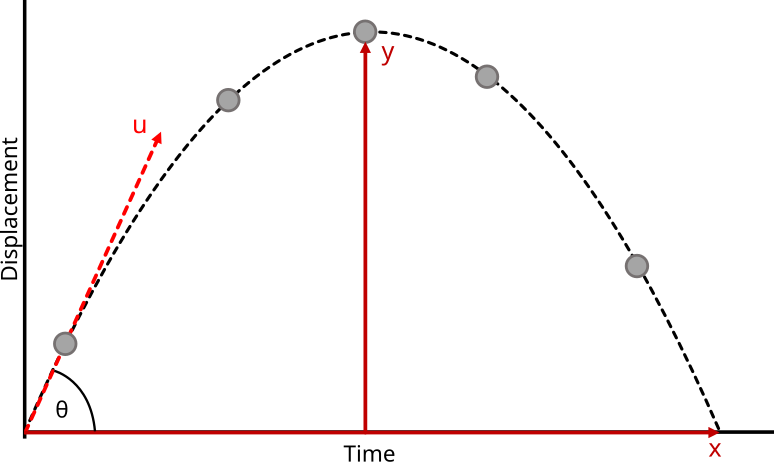
A projectile launched at angle θ follows a parabolic path when air resistance is neglected. The diagram labels u cos θ and u sin θ, the maximum height, and the horizontal range, matching the kinematic treatment of independent components and shared time. The visual aligns with the assumptions used for OCR problems. Source.
Horizontal component (uₓ): motion with constant velocity.
Vertical component (uᵧ): motion with constant acceleration.
These components are connected only through time, which is common to both directions.
Resolving Velocity into Components
When a projectile is launched with an initial velocity u at an angle θ above the horizontal, trigonometric relationships are used to find its components.
EQUATION
—-----------------------------------------------------------------
Horizontal component (uₓ) = u cos θ
u = initial velocity (m s⁻¹)
θ = launch angle (degrees or radians)
Vertical component (uᵧ) = u sin θ
uᵧ = initial vertical velocity (m s⁻¹)
—-----------------------------------------------------------------
Once resolved, each component can be analysed independently using SUVAT equations, provided acceleration is constant.
A projectile’s path shape, maximum height, and range can then be derived through these independent motions.
Horizontal Motion: Constant Velocity
The absence of horizontal forces means no acceleration acts horizontally.
EQUATION
—-----------------------------------------------------------------
Horizontal displacement (sₓ) = uₓ t
sₓ = horizontal distance or range (m)
uₓ = horizontal velocity (m s⁻¹)
t = time of flight (s)
—-----------------------------------------------------------------
Horizontal displacement increases linearly with time. This relationship is fundamental in determining a projectile’s range when combined with vertical motion analysis.
Vertical Motion: Constant Acceleration
The vertical component is subject to uniform acceleration due to gravity. The acceleration a is replaced by –g (acting downwards). The standard SUVAT equations apply:
EQUATION
—-----------------------------------------------------------------
sᵧ = uᵧ t + ½ a t²
vᵧ = uᵧ + a t
vᵧ² = uᵧ² + 2 a sᵧ
sᵧ = vertical displacement (m)
uᵧ = initial vertical velocity (m s⁻¹)
vᵧ = final vertical velocity (m s⁻¹)
a = acceleration (m s⁻²), here −g
t = time (s)
—-----------------------------------------------------------------
These equations allow prediction of how the vertical velocity and position of the projectile change with time.
Between these two analyses lies the time of flight, which links horizontal and vertical behaviour.
Time of Flight and Symmetry of Motion
The time of flight is the total time the projectile remains in the air. For a projectile launched and landing at the same height, the vertical displacement (sᵧ) over the full motion is zero.
Time of flight: The total duration between launch and when the projectile returns to its original vertical level.
Vertical motion is symmetrical: the time taken to rise to maximum height equals the time taken to fall back to the same level. Thus, the time of flight depends on the vertical velocity and gravity.
EQUATION
—-----------------------------------------------------------------
Time of flight (t) = (2 uᵧ) ⁄ g
t = total flight time (s)
uᵧ = initial vertical velocity (m s⁻¹)
g = acceleration due to gravity (m s⁻²)
—-----------------------------------------------------------------
Time of flight provides the link needed to determine range and other trajectory features.
Maximum Height
The maximum height occurs when the vertical velocity becomes zero at the top of the trajectory. The following relationship determines this point.
EQUATION
—-----------------------------------------------------------------
Maximum height (H) = (uᵧ²) ⁄ (2 g)
H = maximum vertical height (m)
uᵧ = initial vertical velocity (m s⁻¹)
g = acceleration due to gravity (m s⁻²)
—-----------------------------------------------------------------
At this instant, the projectile’s upward motion ceases momentarily before gravity accelerates it downward again.
Range of a Projectile
The range is the total horizontal distance travelled before the projectile lands back at its original vertical level.
By combining the equations for horizontal displacement and time of flight, a useful expression for range is obtained.
EQUATION
—-----------------------------------------------------------------
Range (R) = (u² sin 2θ) ⁄ g
R = horizontal range (m)
u = initial launch velocity (m s⁻¹)
θ = launch angle (degrees or radians)
g = acceleration due to gravity (m s⁻²)
—-----------------------------------------------------------------
The range depends on both the launch velocity and the launch angle. Maximum range on level ground occurs when θ = 45°, as this gives the largest value of sin 2θ.
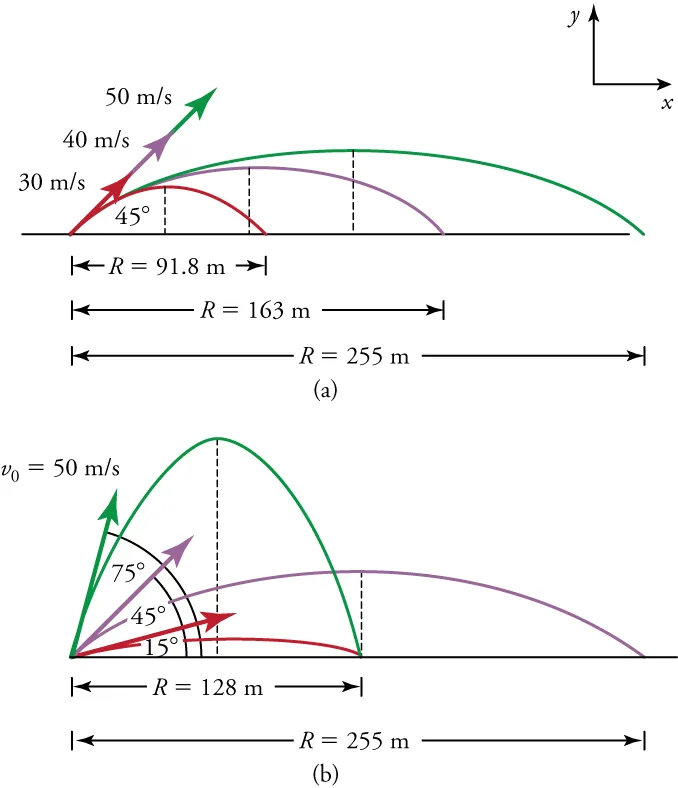
The figure compares projectile trajectories for different initial speeds and launch angles on level ground, highlighting how R=u2sin2θ/gR = u^2 \sin 2θ / gR=u2sin2θ/g governs horizontal distance. It clearly shows the symmetry of complementary angles (e.g., 15° and 75°) yielding equal ranges in the ideal model. Minor extra annotations are included but consistent with OCR-level treatment. Source.
Trajectory Shape and Motion Analysis
Each point on the trajectory corresponds to a different time t, with the following relationships holding:
The horizontal position increases linearly with time.
The vertical position changes quadratically with time, forming a parabolic curve.
When plotting height against horizontal distance, the path follows a parabola because the horizontal displacement increases uniformly while vertical displacement varies as t².
This can be shown algebraically by substituting t = sₓ ⁄ (u cos θ) into the vertical motion equation, linking the two directions and producing a single equation for the trajectory shape.
Trajectory equation: A mathematical relationship expressing vertical displacement in terms of horizontal displacement for a projectile under uniform gravity.
Understanding this relationship enables prediction of where a projectile will be at any point in its flight, an essential part of motion analysis in both experimental and theoretical contexts.
Real-World Applications and Experimental Considerations
Trajectory analysis supports understanding of diverse situations such as:
Ballistics, where accurate range predictions are essential.
Sports physics, including the flight of a ball or javelin.
Engineering, for design of launch mechanisms and safety assessments.
In laboratory experiments:
Data-loggers and video analysis can be used to measure projectile motion precisely.
Graphs of height vs. horizontal distance or velocity vs. time validate model assumptions.
Deviations from theoretical parabolic motion reveal real-world effects like air resistance or uneven gravitational fields.
Analysing trajectories using component vectors and kinematic equations therefore forms the foundation of accurate motion prediction, fulfilling the OCR specification requirement for this subsubtopic.
FAQ
Small variations in initial velocity, launch angle, and air resistance have a large effect on measured range.
Even minimal air resistance slows the projectile, reducing both horizontal speed and time aloft. Launch angle errors of just a few degrees can cause noticeable range differences, particularly near the optimal 45° point.
In addition, uneven launch or landing surfaces, imperfect timing, and non-instantaneous release all reduce agreement between theoretical and observed ranges. Careful calibration of apparatus and consistent measurement technique are vital for accuracy.
The projectile’s motion results from two independent effects:
A constant horizontal velocity (no horizontal forces).
A constant vertical acceleration due to gravity.
Because vertical displacement changes with the square of time (s ∝ t²) while horizontal displacement changes linearly (s ∝ t), their combination produces a parabola.
A circular path would require a constant inward force acting perpendicular to motion, which does not exist in projectile motion.
If a projectile is launched from above ground level, it remains in the air longer because it has further to fall under gravity.
This increases time of flight and, since horizontal velocity remains constant, range also increases.
Conversely, if launched from below the landing point, the time aloft and range both decrease. The simple range equation R = (u² sin 2θ) / g only applies for level launch and landing heights; for other cases, a modified quadratic treatment of vertical motion is required.
In the equation R = (u² sin 2θ) / g, the term sin 2θ determines range for a given speed.
Because sin 2θ = sin (180° − 2θ), complementary angles such as 30° and 60° yield identical sine values. Hence, their ranges are equal provided air resistance is neglected.
However, the flight time and maximum height differ: the higher angle produces greater height and longer air time, while the lower angle gives a flatter, quicker trajectory.
Data-loggers and motion sensors record the position and velocity of a projectile at regular intervals.
A typical procedure involves:
Attaching reflective markers to the projectile or tracking it via video analysis.
Using software to plot displacement–time and velocity–time graphs.
Comparing the experimental curve with theoretical parabolic predictions.
Small deviations from the ideal shape indicate air resistance or timing inaccuracies, providing a clear visual validation of the projectile model’s assumptions.
Practice Questions
Question 1 (2 marks)
A ball is thrown horizontally from the top of a 20 m high cliff with a speed of 12 m s⁻¹.
State two assumptions that must be made for the motion of the ball to be treated as ideal projectile motion.
Mark Scheme
Air resistance is negligible. (1)
Acceleration due to gravity is constant and acts vertically downwards. (1)
(Allow “no horizontal forces act” as an alternative to either mark.)
Question 2 (5 marks)
A projectile is launched from ground level with a speed of 18 m s⁻¹ at an angle of 40° to the horizontal.
(a) Show that the time of flight is approximately 2.35 s. (2)
(b) Calculate the horizontal range of the projectile. (2)
(c) Explain, without further calculation, why the range would decrease if air resistance were not neglected. (1)
Mark Scheme
(a)
Time of flight t = (2 u sin θ) / g (1)
Substitution: (2 × 18 × sin 40°) / 9.81 = 2.35 s (1)
(b)
Range R = u cos θ × t (1)
Substitution: 18 × cos 40° × 2.35 = 32.4 m (accept 32 m to 33 m) (1)
(c)
Air resistance reduces horizontal velocity (or causes energy loss), so the projectile travels a shorter horizontal distance before landing. (1)

