OCR Specification focus:
‘Use density = mass ÷ volume for solids, liquids and gases; handle unit conversions carefully.’
Density is a fundamental physical property that links an object’s mass to its volume, influencing how substances behave in fluids, interact with forces, and determine buoyancy. Understanding and calculating density accurately is vital for analysing materials in physics and engineering.
Understanding Density
Density describes how much mass is contained within a given volume. It enables direct comparison of substances regardless of size or quantity. The denser an object, the more tightly its matter is packed.
Density: The mass per unit volume of a substance, indicating how compactly its particles are arranged.
In physics, this property applies universally to solids, liquids, and gases, though the degree of compressibility and structural bonding between particles differs significantly across these states of matter.
The Density Equation
To quantify density, the OCR specification requires familiarity with the fundamental relationship between mass and volume.
EQUATION
—-----------------------------------------------------------------
Density Equation (ρ) = mass ÷ volume
ρ = m / V
ρ (rho) = Density, measured in kilograms per cubic metre (kg m⁻³)
m = Mass, measured in kilograms (kg)
V = Volume, measured in cubic metres (m³)
—-----------------------------------------------------------------
Between substances of equal volume, the one with the greater mass will have a higher density. Conversely, for equal masses, the substance occupying a larger volume will exhibit a lower density.
Conceptualising Mass and Volume
Mass
Mass represents the quantity of matter in an object and remains constant regardless of location. It is measured using a balance or scale, independent of gravitational effects.
Volume
Volume refers to the amount of three-dimensional space an object occupies.
For regular solids, it can be calculated geometrically (e.g., cube, sphere, cylinder).
For irregular solids, displacement of fluid is commonly used to determine volume accurately.
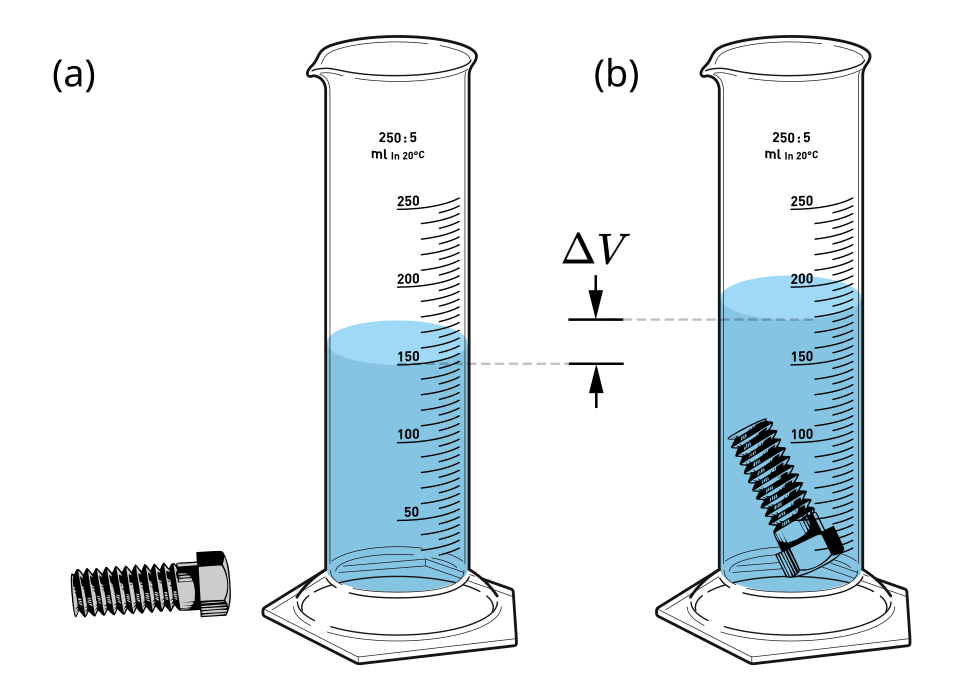
A clear diagram showing the displacement method: the object is submerged and the rise in liquid level gives the object’s volume. This enables density calculation via ρ = m/V once mass is measured. Labels are minimal and placement-friendly for OCR A-Level. Source.
For liquids and gases, volume is measured using calibrated containers or by applying gas laws when necessary.
These quantities form the basis of density determination in laboratory and practical contexts.
Units and Conversions
Accurate unit handling is essential in density problems, as required by the OCR specification. Density can appear in multiple equivalent forms depending on the system of measurement.
Common units include:
kg m⁻³ — the SI unit, used for standard calculations.
g cm⁻³ — often used in laboratory contexts and material data tables.
To convert between these:
1 g cm⁻³ = 1000 kg m⁻³.
Students must always ensure consistency of units across mass and volume before substituting into equations. Failure to convert units properly is a frequent cause of numerical errors in examinations.
Density in Different States of Matter
Solids
Particles in solids are closely packed in fixed positions, resulting in high densities. Metals such as iron or lead exhibit large densities because of their atomic arrangement and small interatomic spacing. The structural rigidity of solids ensures minimal change in density under normal conditions.
Liquids
In liquids, particles are loosely bonded, allowing flow while maintaining moderate density. Liquids are almost incompressible, so their density varies only slightly with temperature. Water, with a density of approximately 1000 kg m⁻³ at 4 °C, serves as a useful reference standard.
Gases
Gases have widely spaced particles and are highly compressible, giving them low densities that depend strongly on temperature and pressure. For example, air has a density near 1.2 kg m⁻³ under standard conditions but decreases with altitude or temperature increase.
Practical Measurement of Density
Accurate measurement of density relies on obtaining reliable values of mass and volume.
For Solids
Measure mass using a high-precision balance.

A laboratory analytical balance fitted with a density determination kit for solids. The sample’s apparent mass in fluid enables volume and density via ρ = m/V. This photo includes equipment specifics beyond the syllabus but illustrates the same underlying method. Source.
Determine volume:
For regular shapes, calculate geometrically using measured dimensions.
For irregular shapes, immerse in water in a graduated cylinder; the volume of displaced water equals the object’s volume (Archimedes’ principle).
For Liquids
Measure a known volume using a pipette, burette, or measuring cylinder.
Record the mass using a balance by subtraction (container + liquid minus empty container).
For Gases
Capture a measured volume of gas in a gas syringe or inverted burette.
Measure mass difference before and after gas introduction in a sealed container.
Temperature and pressure must be recorded, as both affect gas density significantly.
These experimental methods are fundamental to laboratory verification of density relationships and material identification.
Factors Affecting Density
Several physical factors influence measured density values:
Temperature: Increasing temperature typically decreases density for solids and liquids as thermal expansion increases volume.
Pressure: For gases, increased pressure compresses particles closer together, increasing density.
Impurities or composition: The presence of dissolved substances or alloying elements can raise or lower density depending on their own densities and interactions.
Recognising and controlling these variables is essential for experimental accuracy.
Applications of Density
Density plays a critical role in explaining many observable physical phenomena and practical applications:
Floating and sinking: An object floats if its average density is less than that of the surrounding fluid.
Material selection: Engineers choose materials with appropriate densities for structural strength or lightweight design.
Fluid behaviour: Variations in density cause convection currents and buoyancy effects, central to thermodynamics and meteorology.
Identification of substances: Measuring density can help confirm the purity or identity of materials, such as metals or liquids in industrial processes.
Understanding these contexts strengthens conceptual links between theoretical knowledge and real-world physical systems.
Summary of Key Points
Density links mass and volume through the equation ρ = m / V.
It applies to solids, liquids, and gases, with characteristic differences in particle arrangement.
Correct unit conversions and consistent measurements are essential for accuracy.
Environmental factors such as temperature and pressure influence density, particularly in fluids.
Density underpins numerous physical and engineering principles, from buoyancy to material analysis.
FAQ
Temperature changes particle spacing differently across states of matter.
In solids, slight thermal expansion causes a small increase in volume, leading to a minor decrease in density.
In liquids, density decreases more noticeably as particles move apart with heat, though the effect is still moderate.
In gases, density is highly sensitive to temperature because particles move rapidly and expand freely, dramatically reducing density when heated.
Water molecules form hydrogen bonds that create an open hexagonal structure as ice forms.
When water cools from room temperature, molecules move closer until 4 °C, where maximum packing occurs.
Below this, further cooling promotes the open structure typical of ice, reducing density and allowing ice to float.
Small samples are best measured using micropipettes and analytical balances for precise mass and volume readings.
Alternatively:
Pycnometers determine liquid or powdered sample density by comparing displaced fluid mass.
Gas pycnometers use pressure change to calculate volume of minute solid samples.
These methods minimise error when handling quantities too small for conventional measuring cylinders.
Density serves as a fingerprint property for materials.
By measuring an object’s mass and volume, its density can be compared with standard reference tables.
Metals, polymers, and ceramics each have distinct density ranges.
Matching measured density to known values helps confirm composition or detect impurities.
It’s a quick, non-destructive test often used before more advanced analyses like spectroscopy.
High-precision instruments ensure smaller measurement uncertainties in both mass and volume.
Analytical balances measure to 0.0001 g, minimising rounding and parallax errors.
Volumetric pipettes and burettes improve volume accuracy over basic cylinders.
Digital callipers or micrometers provide accurate dimensional data for regular solids.
Together, these tools enhance the reliability of calculated density values and reduce experimental error propagation.
Practice Questions
Question 1 (2 marks)
A small metal cube has a mass of 0.048 kg and a volume of 6.0 × 10⁻⁶ m³.
(a) Calculate the density of the metal in kg m⁻³.
(b) State one reason why the measured density might differ slightly from the known value of the pure metal.
Mark Scheme – Question 1
(a)
• Correct use of the density equation: ρ = m / V (1 mark)
• Substitution and calculation: ρ = 0.048 / (6.0 × 10⁻⁶) = 8.0 × 10³ kg m⁻³ (1 mark)
(b)
• Any one valid reason, e.g. impurities in the sample, measurement error in mass or volume, air bubbles, or temperature variation (1 mark)
Question 2 (5 marks)
A student investigates the density of an irregularly shaped plastic object.
She measures its mass using an electronic balance as 72.4 g. She then immerses it in a measuring cylinder partly filled with water. The water level rises from 45.0 cm³ to 76.5 cm³.
(a) Calculate the density of the object in g cm⁻³. (3 marks)
(b) Suggest two possible sources of error in this experiment and explain how each could affect the result. (2 marks)
Mark Scheme – Question 2
(a)
• Correct use of ρ = m / V (1 mark)
• Correct volume determination: ΔV = 76.5 – 45.0 = 31.5 cm³ (1 mark)
• Substitution and calculation: ρ = 72.4 / 31.5 = 2.30 g cm⁻³ (1 mark)
(b)
• Identifies two valid sources of error such as:
– Parallax error when reading the water level (1 mark)
– Water droplets remaining on the object or trapped air bubbles (1 mark)
• Each explanation must link to how it affects the result, e.g. parallax error gives incorrect volume reading, air bubbles increase apparent volume and reduce calculated density (1 mark per valid explanation, max 2 marks).

