Understanding the number of peaks in a quantitative distribution helps reveal underlying patterns, potential subgroups, and the overall behavior of the data, supporting accurate, context-driven interpretation.

Exploring the Number of Peaks in a Distribution

The shape of a distribution is one of the central components of describing quantitative data. One especially meaningful aspect of shape is the number of modes, or peaks, that appear when the data are graphed using displays such as histograms, dotplots, or stem-and-leaf plots. Each mode represents a value or range of values where observations tend to cluster. Recognizing whether a distribution is unimodal, bimodal, or uniform helps analysts interpret data patterns, hypothesize about underlying causes, and identify meaningful differences in subgroups.

This set of histograms illustrates several common distribution shapes, including uniform, unimodal, bimodal, and multimodal patterns. The bottom row highlights how the number of peaks distinguishes different modalities. Additional shapes shown provide helpful broader context for interpreting distribution form. Source.

Unimodal Distributions

A unimodal distribution has one clear peak where values concentrate noticeably more than elsewhere in the distribution. This peak represents the mode and often provides an immediate sense of the most typical or frequent values in the dataset.

A unimodal shape is common in many naturally occurring phenomena, particularly when data cluster around a central point due to consistent underlying processes. When the peak appears at the center and the distribution is roughly symmetric, it may resemble a bell-shaped pattern. However, unimodality does not require symmetry; the distribution may still be skewed left or right while maintaining a single dominant peak. Understanding its mode helps students identify the most common region of data without assuming any particular functional model.

Bimodal Distributions

A bimodal distribution contains two distinct peaks separated by a noticeable dip or valley in frequency.

These three histograms demonstrate how distributions differ when they contain one, two, or three prominent peaks. The middle graph clearly shows a bimodal pattern with two clusters separated by a valley. Multimodality is also included to help students understand how counting peaks extends beyond the bimodal case. Source.

The separation between the modes is typically meaningful. It may reflect categorical distinctions—such as comparing two teaching methods, two geographic regions, or two product types—that influence the values of the quantitative variable. For AP Statistics students, identifying bimodality is crucial for avoiding misleading interpretations. Treating a bimodal dataset as unimodal may obscure important insights, such as when two different groups exhibit different central tendencies. Because bimodal shapes often arise from mixed populations, investigating context is essential to understand why the peaks occur.

Uniform Distributions

A uniform distribution occurs when all values in the dataset occur with approximately equal frequency, producing a flat or nearly flat shape across the range of data. Unlike unimodal or bimodal distributions, a uniform distribution does not contain any meaningful peak.

Uniform distributions signal that observations are spread evenly, with no particular value or region exhibiting dominance.

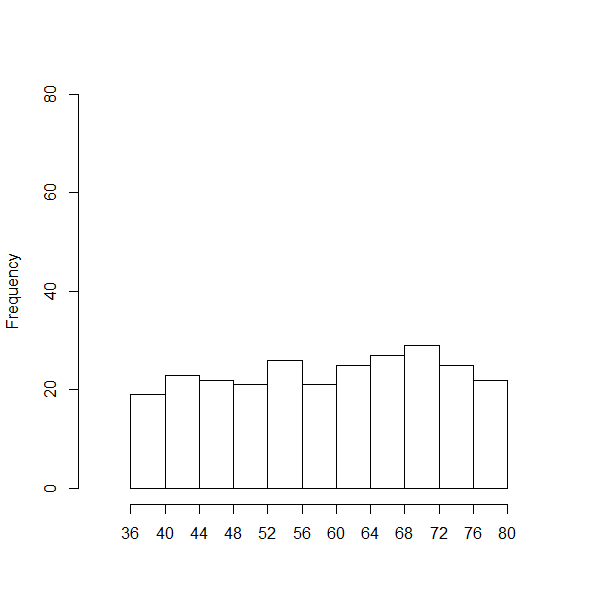
This histogram illustrates a uniform distribution, where bar heights remain approximately equal across the full range of values. The visual shows the absence of a dominant mode, emphasizing even spread. Although the page includes additional plots, this histogram aligns directly with the concept of uniformity discussed in the notes. Source.

Understanding this pattern helps analysts describe situations in which all outcomes are about equally likely or where no concentration of observations appears.

Interpreting Modes and Their Implications

The number of peaks in a distribution does more than classify its shape; it provides essential information for interpretation. A single peak may suggest a consistent underlying process, while two peaks may point to distinct groups or repeated measurement conditions. Uniform patterns highlight a lack of concentration, suggesting that no particular outcome stands out.

Understanding these distinctions helps students better describe patterns in context, aligning with Skill 2.A's emphasis on articulating distribution characteristics. When describing data, students should consider:

• How many modes are present and whether the peaks are clear.

• What the peaks represent in context, such as behavioral patterns, natural variation, or subgroup characteristics.

• Whether the distribution’s appearance suggests uniform behavior or equal likelihood across the domain.

• How the number of peaks influences interpretation, especially when comparing groups or investigating unusual features.

Real-World Scenarios Reflecting Different Shapes

Connecting distributions to realistic scenarios strengthens understanding and promotes accurate contextual interpretation. Unimodal shapes might appear in measurements influenced by a single dominant factor, such as heights of students in the same grade level. Bimodal shapes often occur when combining data from two groups with different characteristics, such as travel times from urban and rural areas. Uniform shapes arise in structured or random settings, such as simulated data where each outcome is equally probable.

These connections reinforce the idea that the form of a distribution is not arbitrary but instead reflects meaningful features of the data-generating process. Such insight supports deeper reasoning about data and strengthens students' ability to justify claims based on observed patterns.