Understanding how to extend findings from a sample to an entire population is essential for valid statistical reasoning and supports accurate, trustworthy conclusions in studies.

Making Inferences: From Samples to Population

The Purpose of Statistical Inference

Statistical inference allows researchers to use information from a sample to make reasoned statements about a population. Because studying every individual in a population is often impossible, inference provides a structured way to generalize findings beyond the sample actually observed. The quality of these generalizations depends heavily on how the sample was collected and whether randomness was used to reduce bias.

Population is introduced early in statistical studies, and it refers to the complete set of individuals or items of interest.

A sample is the smaller group selected from that population for measurement or observation.

The relationship between sample and population lies at the heart of inference, creating a framework for estimating population characteristics using sample data.

Why Representativeness Matters

A sample must be representative, meaning it reflects the characteristics of the population reasonably well. When the sample resembles the population in composition and variation, conclusions drawn from the sample are more likely to be trustworthy.

A key component of representativeness is random selection, which gives each member of the population an equal chance of being chosen.

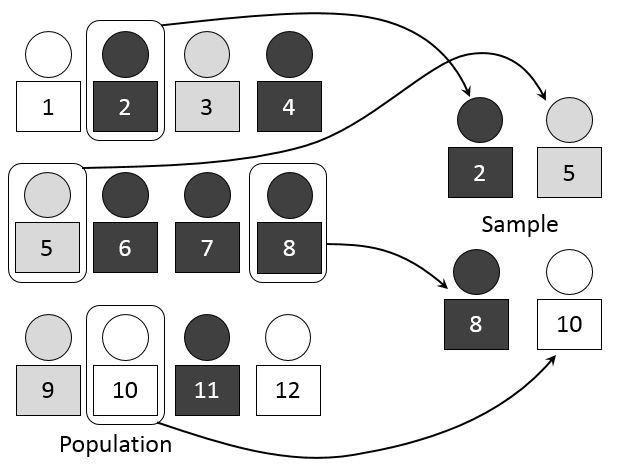
A visual representation of simple random sampling, showing how individuals are chosen randomly from a population to form a representative sample that supports valid inference. Source.

Random selection supports two major goals in inference:

• It helps eliminate systematic error, allowing chance variation to govern which individuals enter the sample.

• It ensures that observed patterns in the sample can plausibly be attributed to population-level patterns.

How Random Sampling Supports Valid Inference

Random sampling methods strengthen inference because they use chance to avoid predictable patterns in sample formation. When randomness is incorporated into data collection:

• Results become less dependent on the choices or preferences of the researcher.

• Observed sample statistics can be treated as unbiased estimates of the corresponding population parameters.

• Probability theory can be applied to quantify uncertainty in sample-based estimates.

This link between randomness and inference is foundational in AP Statistics, supporting the use of sampling distributions, margin of error, and confidence intervals in later topics.

Sampling Variability and Uncertainty

Every sample differs from every other possible sample due to sampling variability, the natural variation that arises purely by chance. Because of this variability, no sample perfectly mirrors the population. Inference provides tools for measuring how far off a sample is likely to be from the true population value.

Researchers acknowledge and manage sampling variability by:

• Using sufficiently large sample sizes.

• Relying on random methods.

• Interpreting results within a framework of probability rather than certainty.

These considerations allow students to understand why two samples from the same population may yield slightly different results and how inference accommodates this uncertainty.

Limits of Observational Data in Making Causal Claims

Inference from samples to populations concerns generalization, not causation. While random selection supports generalization, it does not permit claims about cause and effect. The syllabus emphasizes that observational studies, which involve no imposed treatments, cannot reliably establish causality. Observational studies may reveal associations, but uncontrolled variables can produce misleading relationships.

Important limitations of observational studies:

• They cannot eliminate confounding variables.

• They do not provide the controlled conditions needed to isolate explanatory factors.

• They permit inference about populations only if random selection is used.

Because of these constraints, researchers rely on experimental design (covered elsewhere in the syllabus) to make causal claims.

Key Components of Drawing Valid Inferences

To ensure that inferences are accurate and statistically meaningful, researchers focus on several essential conditions:

1. Use of Random Selection

• Ensures sample representativeness.

• Allows the use of probability-based reasoning.

• Prevents systematic bias in determining who participates.

2. Appropriate Sample Size

• Larger samples reduce sampling variability.

• Inference becomes more precise as sample size increases.

3. Clearly Defined Population and Sampling Frame

• The target population must be specified before collecting data.

• The sampling frame must closely match the population to avoid undercoverage.

4. Awareness of Study Design Limitations

• Observational studies support generalization only.

• Causal conclusions require well-designed experiments with random assignment, not random sampling.

The Role of Sampling Distributions in Inference

While formal work with sampling distributions occurs later in the course, the conceptual foundation begins here. A sampling distribution describes the values a sample statistic can take across all possible samples from the population.

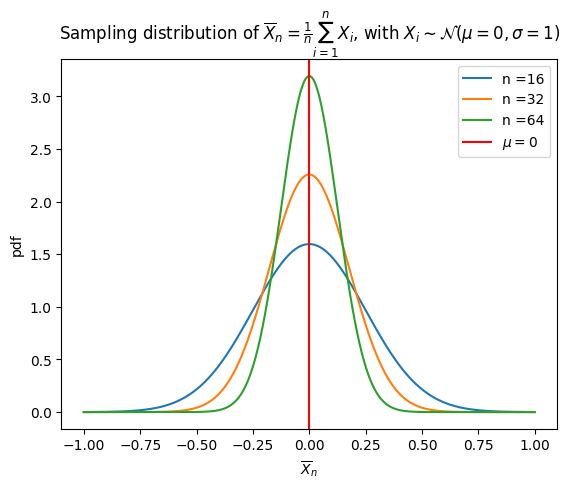
Sampling distributions of the sample mean for a normal population, showing how larger sample sizes narrow the distribution and reduce sampling variability, supporting more precise inference. Source.

Understanding this idea conceptually helps students appreciate why:

• Randomness allows predictable long-run behavior.

• Inference methods rely on probability models.

• Individual sample results must be interpreted within a range of plausible outcomes.

These ideas build toward more advanced inferential techniques, reinforcing why high-quality data collection is essential from the outset.