AP Syllabus focus:
‘Essential Knowledge: VAR-3.E.2 explains how random assignment of treatments to experimental units empowers researchers to infer that observed changes are significant enough to unlikely be due to chance, categorizing them as statistically significant.’
Random assignment is central to valid experimentation because it distributes uncontrolled variables evenly across treatment groups, allowing researchers to attribute meaningful differences in outcomes to the treatments rather than chance.
The Role of Random Assignment in Experiments
Random assignment is a defining feature of a well-designed experiment, ensuring that each experimental unit has an equal chance of receiving any treatment.
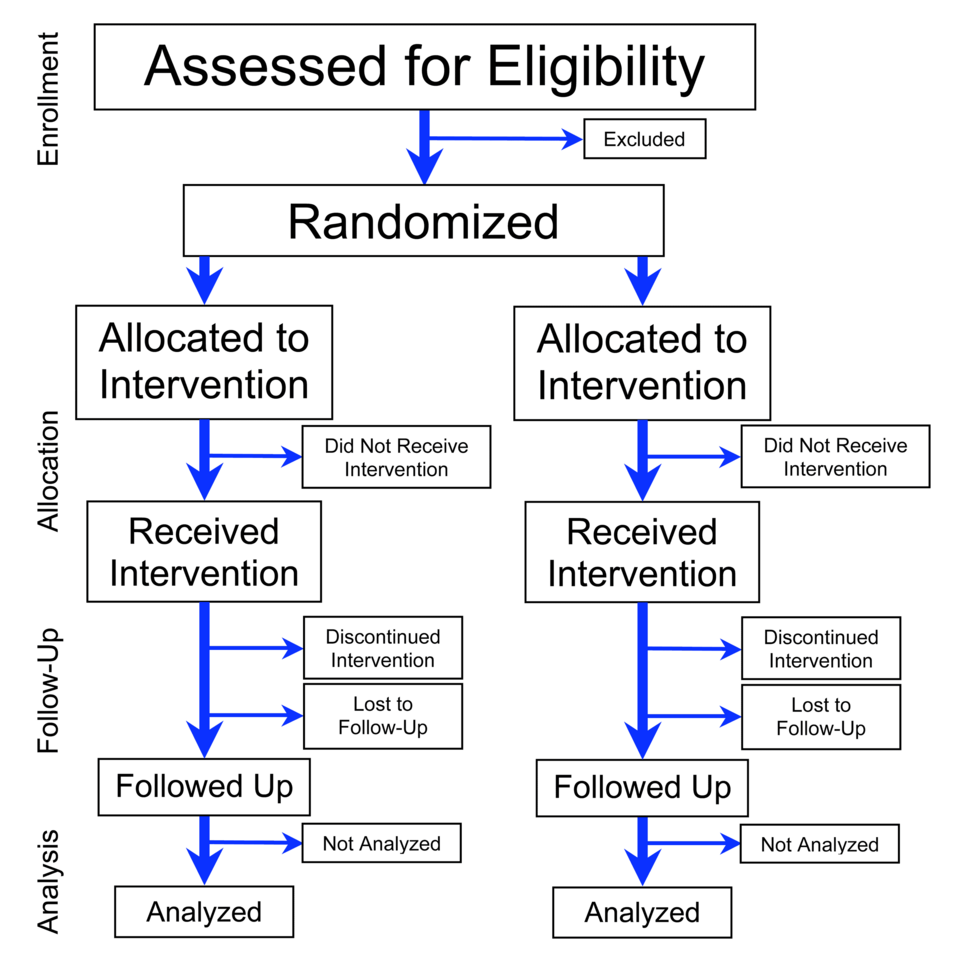
Flowchart of a parallel randomized trial showing how participants are assigned by chance into intervention groups, illustrating the central role of random assignment in creating comparable groups. The diagram includes additional follow-up and analysis steps beyond the syllabus focus but situates the randomization process within the broader experimental structure. Source.
Its purpose is to create groups that are similar with respect to all variables except the explanatory variable, enabling researchers to isolate treatment effects accurately.
Random Assignment: The process of using a chance mechanism to assign experimental units to different treatment groups so the groups are expected to be comparable at the outset.
Random assignment differs from random selection, which is concerned with sampling individuals from a population. Only random assignment supports causal inference, because it balances both known and unknown confounding variables across treatment groups.
Why Random Assignment Allows Inferences About Significance
The AP specification emphasizes that random assignment allows researchers to determine whether observed differences between treatment groups are large enough that they are unlikely to have occurred by chance alone. When differences are sufficiently large under a random assignment framework, researchers describe them as statistically significant.
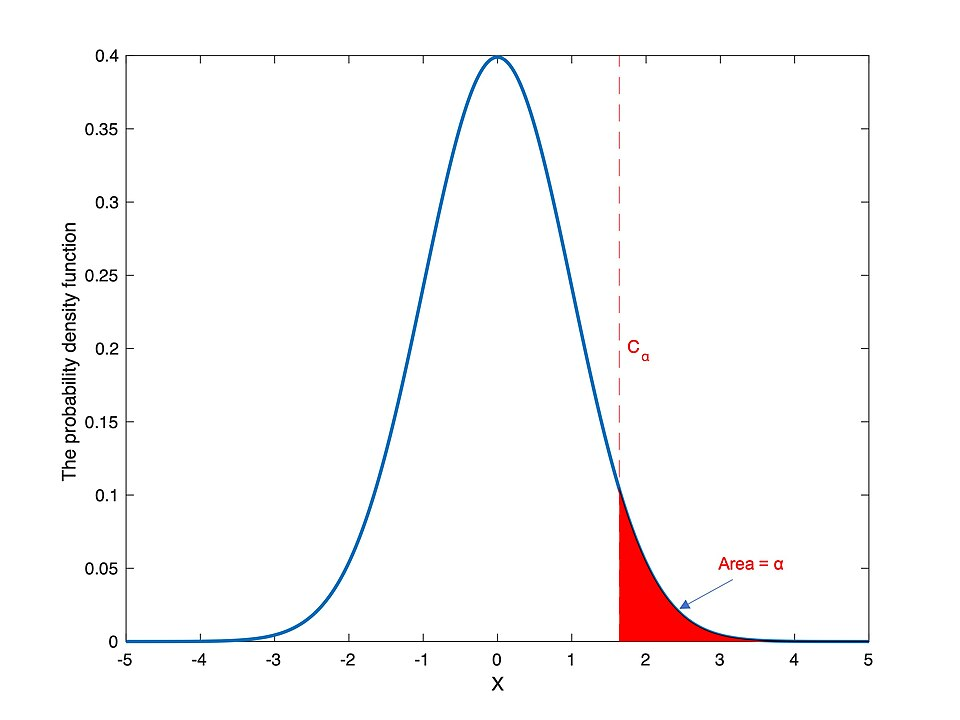
Standard normal curve showing a one-tailed critical value and shaded significance level α, illustrating how statistically significant results are those unlikely to occur by chance alone. Although presented generally for hypothesis testing, the diagram aligns with the syllabus focus on interpreting significance in experiments. Source.
Statistically Significant: A difference in outcomes between treatment groups that is unlikely to occur simply as a result of random chance when treatments have been randomly assigned.
This concept builds the foundation for attributing observed differences in response variables directly to the treatment itself. Without random assignment, researchers cannot separate treatment effects from confounding influences.
How Random Assignment Supports Causal Claims
Creating Comparable Groups
Random assignment distributes uncontrolled sources of variability evenly, making treatment groups similar in composition. This similarity means that any consistent difference observed in their response variables more plausibly reflects the effect of the treatment rather than the influence of external factors.
Eliminating Systematic Bias
Because assignment relies solely on chance:
No participant or researcher controls who receives which treatment.
Systematic differences between groups are minimized.
Confounding variables become less influential because they are expected to be balanced across groups.
A properly executed random assignment mechanism ensures fairness and neutrality in the experimental process.
Methods of Implementing Random Assignment
Researchers use structured chance procedures to assign treatments. Common methods include:
Random number generators to match units to treatments.
Random digits tables to create unbiased assignments.
Physical methods, such as drawing slips of paper or flipping coins.
These methods preserve unpredictability and guarantee that each unit has the same probability of receiving each treatment.
A structured randomization plan reduces the likelihood that human judgment—often unknowingly biased—affects treatment assignment.
Random Assignment and Variability in Outcomes
Random assignment supports valid statistical inference by creating a theoretical distribution of possible outcomes under the assumption that the treatment has no effect. This distribution is the reference for determining significance.
Key Features of Variability Under Random Assignment
Treatment groups vary in composition only by chance, not systematically.
Any difference in outcomes when the treatment truly has no effect should be small.
Large differences suggest that chance alone is not a reasonable explanation.
This logic underlies the inferential procedures taught in AP Statistics, such as simulation-based tests for significance in experiments.
Determining Statistical Significance Through Random Assignment
Conceptual Framework
Random assignment allows researchers to construct what would happen in repeated random assignments. If the observed difference between groups is extreme relative to what would typically occur:
The result is considered statistically significant.
A treatment effect becomes the most plausible explanation.
Researchers evaluate significance by comparing the observed difference in group outcomes to the distribution of differences generated through repeated random assignments or theoretical probability models.
Key Indicators of Statistical Significance
The observed difference is far from zero relative to expected random variation.
Only a small proportion of the random assignment distribution produces differences as large as or larger than the observed one.
The chance that such a difference arose randomly is low, strengthening the evidence for a treatment effect.
The Relationship Between Random Assignment and Causality
Because random assignment balances confounders, a statistically significant difference between treatment groups indicates evidence of a causal relationship. AP Statistics emphasizes that:
Causality cannot be inferred from observational studies.
Well-designed experiments using random assignment allow causal conclusions when significance is demonstrated.
This is the central reason random assignment is required for experiments intended to establish cause-and-effect relationships.
Summary of Core Principles for AP Students
Random assignment creates comparable treatment groups.
It supports causal inference by reducing confounding influences.
It enables researchers to determine whether observed differences are statistically significant.
Significance under random assignment suggests the treatment meaningfully affects the response variable.
Random assignment is essential for interpreting experimental outcomes within the AP Statistics framework.
FAQ
Dividing participants evenly without using chance can still introduce systematic differences, because the researcher may unintentionally place certain types of individuals in specific groups.
Random assignment removes this discretion entirely by giving every participant the same probability of receiving each treatment. This ensures balance not only in visible characteristics but also in unmeasured or unknown variables, which is essential for making reliable causal claims.
Any procedure that ensures unpredictability and equal probability is acceptable. Common methods include:
• Computer-generated random number lists
• Random digits tables
• Drawing lots or shuffling cards
The key requirement is that the mechanism is free from human influence and produces genuinely random allocations.
Yes, but its balancing effect is less reliable in small groups. Chance may produce uneven distributions of important characteristics.
Researchers often:
• Increase sample size when possible
• Use blocking or stratifying before random assignment to improve balance
• Conduct sensitivity checks to understand how imbalance could affect results
Even with small samples, random assignment still protects against intentional or systematic bias.
Assumptions about group similarity can be misleading. People often overlook subtle or hidden variables that affect outcomes.
Random assignment protects the study from these unknown influences by equalising groups automatically, rather than relying on researcher judgement. This prevents overconfidence in perceived equivalence between participants.
Simulation-based tests imitate the random allocation process many times to estimate what differences in outcomes would look like if the treatment had no effect.
By comparing the observed difference to this simulated distribution, researchers can judge whether the result is unusually large. Random assignment is what makes these simulations valid, because the process being simulated matches the actual design of the experiment.
Practice Questions
Question 1 (1–3 marks)
A researcher is conducting an experiment to test whether a new fertiliser increases plant height. Each plant in the study is assigned to either the new fertiliser or a standard fertiliser using a random number generator.
Explain why random assignment is important in this experiment.
Question 1 (1–3 marks)
Award up to 3 marks:
1 mark for stating that random assignment creates comparable groups.
1 mark for explaining that it balances confounding variables between groups.
1 mark for stating that it allows differences in plant height to be attributed to the fertiliser rather than other factors.
Question 2 (4–6 marks)
A school wants to determine whether a new revision programme improves students’ test scores compared with the usual study routine. Sixty students volunteer to participate. The school randomly assigns 30 students to the new revision programme and 30 to the usual routine. After six weeks, all students complete the same test.
(a) Explain how random assignment contributes to the validity of this experiment.
(b) Students assigned to the new revision programme scored, on average, 6 points higher than those in the usual routine group. Describe how researchers would decide whether this difference is statistically significant.
(c) Based on your answer to part (b), explain when it would be appropriate to conclude that the revision programme causes improved test performance.
Question 2 (4–6 marks)
Part (a) (2 marks total)
1 mark for stating that random assignment distributes confounding variables evenly across groups.
1 mark for explaining that this helps ensure that any difference in scores is due to the revision programme rather than pre-existing differences.
Part (b) (2 marks total)
1 mark for stating that researchers compare the observed difference with what would be expected by chance under repeated random assignments or simulations.
1 mark for explaining that if the observed difference is unlikely to occur by chance, it is considered statistically significant.
Part (c) (2 marks total)
1 mark for stating that causal conclusions require statistically significant differences between groups.
1 mark for stating that significance under random assignment provides evidence that the revision programme caused the improvement.

