AP Syllabus focus:
‘VAR-4.C.1: Introduce the concept of joint probability as the likelihood of both events A and B occurring together, represented as P(A ∩ B). Explain the mathematical notation and significance of the intersection of A and B in the context of probability theory.’
Understanding joint probability allows statisticians to quantify how likely it is for two events to occur at the same time, forming a foundation for analyzing relationships between events.
Joint Probability in Probability Theory
Joint probability is central to probability because it describes situations where two conditions must be met simultaneously. It provides a structured way to evaluate how two events relate within the same random process. Whenever two events are considered together, statisticians examine how their overlap influences the likelihood of outcomes.
The Intersection of Events
When events occur within a random process, it is often necessary to assess not just their individual likelihoods but also the likelihood that they occur together. This combined occurrence is known as their intersection, written using the symbol ∩, which visually and conceptually captures the shared region of outcomes belonging to both events.
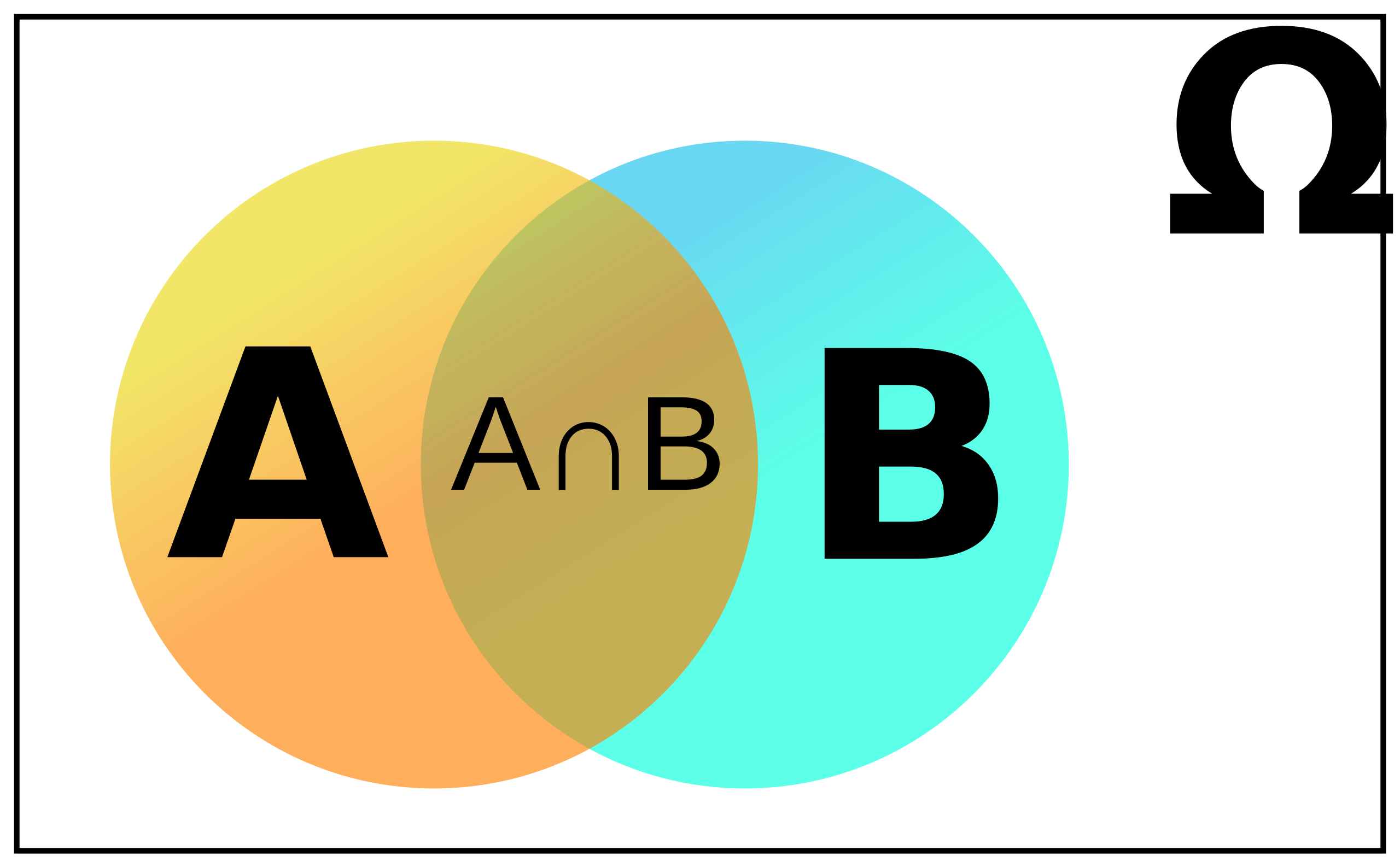
This Venn diagram shows two events A and B inside a sample space rectangle. The shaded region represents the intersection A∩BA \cap BA∩B, where both events occur together. This shared region visually corresponds to the joint probability P(A∩B)P(A \cap B)P(A∩B). Source.
Term: Intersection (A ∩ B) — The set of all outcomes that belong to both event A and event B, representing situations where both events occur simultaneously.
The intersection forms the basis for joint probability, because joint probability quantifies the likelihood of outcomes in this shared set. When students interpret , they are identifying where the characteristics of both events coexist within the sample space.
Representing Joint Probability
Joint probability is expressed using probability notation, which formalizes how statisticians communicate the likelihood of combined events. The notation reinforces precise thinking and ensures consistent interpretation across different probability contexts.
EQUATION
= The intersection, or shared outcomes, of events A and B
This notation highlights that joint probability focuses specifically on the outcomes common to both events. Because of this, joint probability often reflects a smaller probability than that of either event alone, since it is restricted to the overlap rather than the full range of each event.
A clear understanding of the relationship between an event and its intersection with another supports later exploration of additional probability rules, such as those involving unions, complements, or conditional probability.
Interpreting Joint Probability
Interpreting joint probability involves connecting the symbolic notation with how real-world processes behave. Students must visualize the structure of a sample space and understand that two events may overlap fully, partially, or not at all, depending on their characteristics. Joint probability only exists when there is at least one outcome that satisfies both event descriptions.
Conceptualizing Overlap in the Sample Space
To interpret joint probability accurately, students should recognize the sample space as the complete set of possible outcomes for a random process. Events carve out regions within this space, and the intersection represents the region where these event regions overlap. The size of this overlap relative to the size of the entire sample space influences the value of the joint probability.
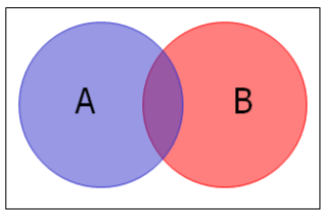
This Venn diagram illustrates two events A and B within a sample space, with the darker central region marking the outcomes belonging to both events. This overlap represents the intersection A∩BA \cap BA∩B, which determines the joint probability. The colored circles also imply the broader union A∪BA \cup BA∪B, extending beyond the focus of this subsubtopic. Source.
Important considerations include:
Event Definitions: How events A and B are described strongly affects the shape and extent of their overlap.
Outcome Structure: Joint probability depends on outcomes, not interpretations; therefore, clear articulation of the events is essential.
Shared Conditions: Joint probability captures scenarios requiring simultaneous satisfaction of multiple conditions.
The Importance of Joint Probability
Joint probability supports deeper probability reasoning because it reveals how events interact, whether they reinforce or restrict one another, and how their relationship influences likelihoods. It also links directly to later topics in conditional and independent probability by providing the foundational concept of an intersection.
Bullet points that help clarify its importance include:
Joint probability quantifies the likelihood of combined requirements in a random process.
It establishes the groundwork for conditional probability by describing the overlap that conditional formulas rely on.
Understanding intersections helps identify when events are mutually exclusive, because mutually exclusive events have no overlap and therefore have a joint probability of zero.
Joint probability is necessary for applying addition and multiplication rules correctly in more advanced probability contexts.
It reinforces the structure of the sample space by requiring students to precisely locate shared outcomes.
Notational Significance
Every element of the notation carries meaning. The P indicates probability, the parentheses define the target event, and the intersection symbol identifies that both events must occur together. Recognizing this structure ensures students avoid common errors, such as confusing intersections with unions or treating joint probability as a simple addition of individual probabilities.
By understanding the notation, definition, and purpose of joint probability, students strengthen their foundational probability skills and build the framework necessary for analyzing more complex event relationships in later topics.
FAQ
Multiplying two probabilities only gives the correct joint probability when the events are independent, meaning the occurrence of one does not influence the other.
For general events, joint probability depends on the size of the actual overlap between events in the sample space, not on a product of their separate probabilities.
A multiplication-based approach without independence can overestimate or underestimate the true joint probability.
No. The intersection of two events represents only the outcomes they share, so it cannot exceed the size of either event alone.
In set terms, the overlap cannot be bigger than the sets it comes from.
This means P(A ∩ B) is always less than or equal to both P(A) and P(B).
The only time they are equal is when one event is entirely contained within the other.
A Venn diagram visually shows whether the regions representing the two events overlap. If there is any shared region, then P(A ∩ B) is greater than zero.
Look for:
• Circles that overlap partially or fully
• A shaded region that represents the intersection
• The absence of overlap, which indicates P(A ∩ B) = 0
Venn diagrams are helpful for conceptualising probability structure before working with numerical values.
A very small but non-zero joint probability indicates that the two events can occur together, but this combined outcome is rare relative to the full sample space.
This can occur when:
• Events share few common outcomes
• The sample size is large and only a small subset fits both events
• The behaviours or characteristics associated with the events seldom coincide
Small joint probabilities often prompt further investigation in real-world studies.
Joint probability reveals how frequently two characteristics or behaviours occur together, which helps identify patterns worth further statistical analysis.
For example, if P(A ∩ B) is substantially larger than expected under independence, this suggests a meaningful association between the events.
Such observations can motivate deeper modelling, such as examining causation, correlation, or subgroup structures in the population.
Practice Questions
Question 1 (1–3 marks)
A survey records whether adults prefer tea (Event A) and whether they also prefer biscuits as a snack (Event B). The probability that an adult prefers both tea and biscuits is 0.31.
(a) State what 0.31 represents in terms of joint probability.
(b) Describe what the intersection A ∩ B means in this context.
Question 1 Mark Scheme (1–3 marks)
(a)
• 1 mark: States that 0.31 is the probability that an adult prefers both tea and biscuits.
(b)
• 1 mark: Correctly explains that A ∩ B represents the adults who prefer tea and also prefer biscuits at the same time.
Total: 2 marks.
Question 2 (4–6 marks)
A wildlife researcher records two behaviours in a species of bird:
• Event A: The bird sings during the early morning.
• Event B: The bird engages in nest-building activity on the same day.
The probability that a randomly observed bird sings in the early morning is 0.62. The probability that it engages in nest-building is 0.48. The probability that it does both on the same day is 0.27.
(a) Identify the joint probability in this scenario.
(b) Determine whether it is possible that a bird performs neither behaviour on a given day. Show your reasoning.
(c) Explain, in context, what the event A ∩ B represents for the researcher.
Question 2 Mark Scheme (4–6 marks)
(a)
• 1 mark: Identifies 0.27 as the joint probability.
(b)
• 1 mark: Calculates or states that P(A ∪ B) = 0.62 + 0.48 − 0.27 = 0.83.
• 1 mark: Concludes that some birds can perform neither behaviour because 1 − 0.83 = 0.17, which is greater than zero.
(c)
• 1 mark: Explains that A ∩ B represents birds that both sing during the early morning and engage in nest-building on the same day.
• 1 mark: Explanation must be contextual and clearly relate to both recorded behaviours.
Total: 5 marks.

